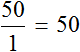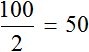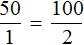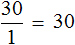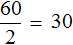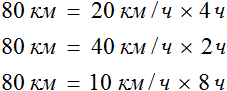Что значит обратно пропорционален

Прямая и обратная пропорциональность

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.

Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.

Прямая пропорциональность

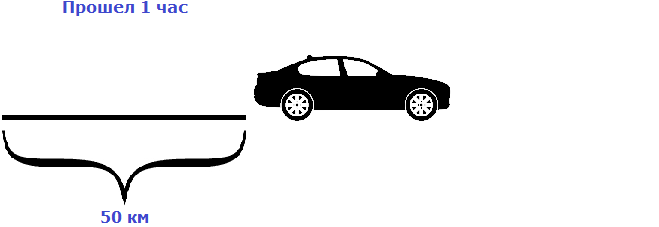
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.

Изобразим на рисунке расстояние, пройденное автомобилем за 1 час

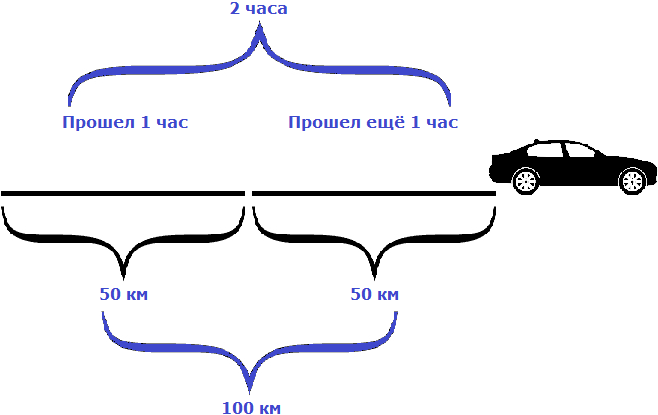
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км

Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.

Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.

Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.

Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.

Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.

В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.

Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50

Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.

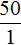
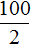
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:

Это отношение можно прочитать следующим образом:

Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.

Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.

Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.

Запишем чему равно отношение тридцати рублей к одному килограмму

Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:

Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.

Обратная пропорциональность

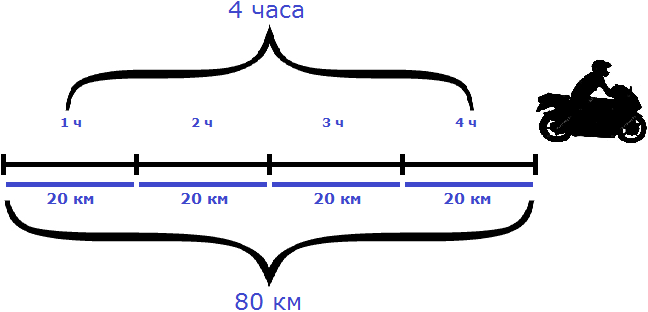
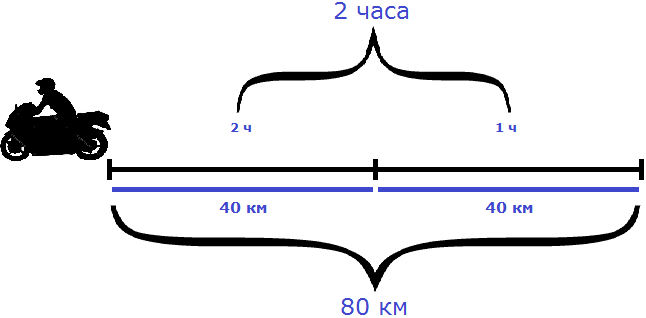
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.

Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:

На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.

Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.

Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.

Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.

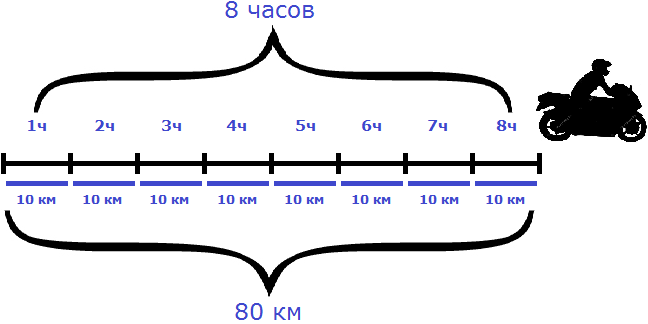
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:

Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.

Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.

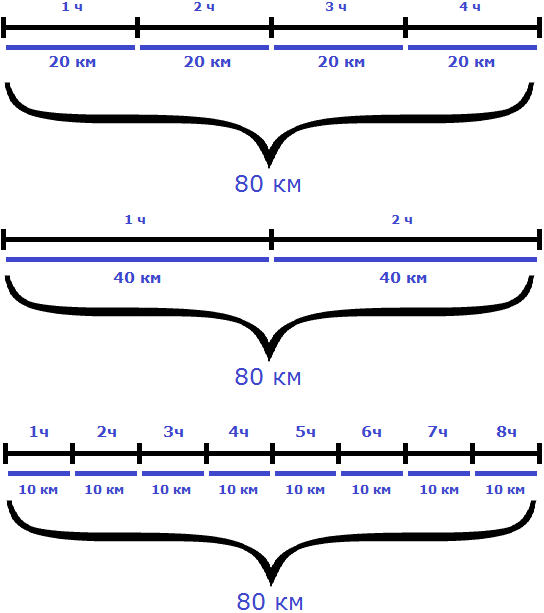
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным

Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

10 thoughts on “Прямая и обратная пропорциональность”

что ценно теория методически верно преподается. очень добрый сайт.

мне теперь всё понятно, большое спасибо сайту

Источник

Презентация к уроку

Аудитория: 6 класс.

I. Организационный момент

II. Мотивация учебной деятельности учащихся

Учитель: Перед Вами молодая семья. Им нужно сделать бюджетный ремонт в ванной комнате. Предлагаю Вам помочь им, используя те знания, которые у Вас есть.

III. Устная работа

Учитель: Проверим Ваши знания».
– Что такое отношение?
– Что показывает отношение?

Учитель: Вспомним, если значения двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. Отношением масс, отношением длин и т.д.
– Что такое пропорция?
– Основное свойство пропорции?

IV. Актуализация знаний

Учитель: Из каких этапов состоит ремонт в ванной комнате? (спросить детей, выслушать их варианты, повторить, что семья молодая и ремонт бюджетный, совместно придти к следующему плану)

План постепенно, по мере рассуждений появляется на слайде. После, вывешивается на доске (заранее распечатать каждый этап).

Учитель: 3 кг потолочной краски в среднем стоят 250 рублей. Им необходимо приобрести 9 кг краски. Сколько будет стоить покупка?

Рассуждают дети. Появляется ответ (750 рублей).

Учитель: Посмотрите на схему, заметили ли Вы зависимость?
Масса краски увеличилась в 3 раза, соответственно стоимость то же увеличилась в 3 раза. Показать стрелки.
Обратить внимание на направление стрелок.
Во сколько раз увеличивается масса краски, во столько же раз увеличивается её стоимость, при условии, что цена на товар остается неизменной.

Учитель: Значит, отношение значений одной величины и отношение значений другой величины по отношению к друг другу?

Рассуждают дети, приходят к ответу: будут равны.

Учитель: Вывод: Отношения соответствующих значений этих величин равны.

Учитель: Напомните, что такое пропорция? Следовательно, пропорция верна.

Учитель: Первая бригада состоит из 8 человек, они могут выложить плитку за 3 дня. Сколько дней будет выполнять эту же работу вторая бригада, работая с той же производительностью труда, состоящая из 4 человек?

Рассуждают дети, приходят к ответу: 6.

Учитель: Посмотрите на схему, заметили ли Вы зависимость?
Количество человек в бригаде уменьшилось в 2 раза, во столько же раз увеличилась количество дней. Показать стрелки.
Обратить внимание на направление стрелок.
Во сколько раз уменьшается число человек, выполняющих с одинаковой производительностью труда работу, во столько же раз увеличивается время выполнения работы, при условии, что объем работы, которую выполняют бригады одинаковый.

Учитель: Значит, отношение значений одной величины и отношение значений другой величины по отношению к друг другу?

Рассуждают дети, приходят к ответу: будут не равны.

Учитель: Значит, отношение значений одной величины и обратное отношение значений другой величины по отношению к друг другу?

Рассуждают дети, приходят к ответу: будут равны.

Учитель: Вывод: Отношение значений одной величины равно обратному отношению соответствующих значений другой величины, следовательно, пропорция верна.

Учитель: Что у нас получилось?

Учитель: Посмотрите, с одной стороны:
Если одна величина увеличивается, то и другая увеличивается во столько же раз, при этом отношение соответствующих значений этих величин – равны. Стрелки при этом направлены в одну сторону.Учитель: С другой стороны:
Если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз, при этом отношение значений одной величины равно обратному отношению соответствующих значений другой величины. Стрелки при этом направлены в разные стороны.Такие величины называют прямо пропорциональными.Такие величины называют обратно пропорциональными.

Учитель: Общий вид Вы видите на слайде. Такая шпаргалка есть у каждого (распечатать каждому). Приложение 1. Она поможет вам при решении задач.

Учитель: Сформулируйте тему сегодняшнего урока.

Рассуждают дети, приходят к ответу: «Прямая и обратная пропорциональные зависимости».

Учитель: Открываем тетради, записываем число и тему урока.

Учитель: Перед молодой семьёй стал выбор плитки. Имеется два вида плитки (лучше показать оригиналы, я показывала квадратную плитку с размерами 20 см х 20 см и прямоугольную плитку 25 см х 36 см, размеры написаны на плитке маркером).

Учитель: Размеры меньшей – 20 см х 20 см. Переведите см в дм.

Рассуждают дети, приходят к ответу: 20 см = 2 дм (подписать маркером на плитке).

Учитель: Форма плитки? Найдите площадь плитки.

Рассуждают дети, приходят к ответу: квадрат, S = 4 дм 2 (подписать маркером на плитке).

Учитель: Размеры большей – 25 см х 36 см. Переведите см в дм.

Рассуждают дети, приходят к ответу: 25 см = 2,5 дм; 36 см = 3,6 дм; (подписать маркером на плитке).

Учитель: Форма плитки? Найдите площадь плитки.

Рассуждают дети, приходят к ответу: квадрат, S = 4дм 2 (подписать маркером на плитке).

V. Первичное усвоение новых знаний

Учитель: «Задачи на пропорциональные зависимости решаются с помощью пропорции».

Учитель: Задачи решаются по следующему алгоритму.

Алгоритм:

1. Составить схему.
2. Неизвестное число обозначить за х.
3. Установить вид зависимости между величинами.
4. Записать пропорцию.
5. Найти её неизвестный член.

Учитель: Составим схему.

Учитель: Неизвестное число обозначим за х.
Учитель: Установите вид зависимости между величинами.
Учитель: Как составить пропорцию? Используйте шпаргалку.
Пригласить к доске одного ребенка решить пропорцию и записать ответ (27 упаковок).

Учитель: Какую плитку выгоднее купить?

Рассуждают дети, приходят к ответу: плитку большей площади.

Учитель: Вернемся к задаче про бригаду. Какую бригаду, выгоднее нанять, если за работу они берут одну и ту же сумму денег?

Рассуждают дети, приходят к ответу: бригаду, состоящую из 8 человек.

VI. Первичная проверка понимания

Учитель: Ребята, какую плитку выгоднее купить мы определили, какую бригаду нанять выбрали. Справились ли мы с поставленной задачей в начале урока?

Учитель: А помогли нам в этом прямая и обратная пропорциональная зависимость. Что показывает прямая пропорциональная зависимость? Обратная? Как составить пропорцию, при решении задач на прямую пропорциональную зависимость? На обратную? А все ли в этом мире находится в пропорциональной зависимости?

Рассуждают дети, приходят к ответу: нет.
Попросить привести примеры, если не получается привести пример: возраст человека и его рост.

VII. Первичное закрепление

Выполнить задание (при условии, что есть интернет).

http://learningapps.org/633824 – Прямая и обратная пропорциональная зависимости.

VII. Домашнее задание

VIII. Рефлексия (подведение итогов занятия)

Учитель: Что сегодня Вы узнали на уроке? Спасибо за урок. Молодцы!

Источник

Обратная пропорциональность. Гипербола

Сейчас мы будем говорить об обратной пропорциональности, или другими словами об обратной зависимости, как о функции.

Мы закрепим понятие функции и научимся работать с коэффициентами и графиками.

А еще мы разберем несколько примеров построения графика функции — гиперболы.

Обратная пропорциональность — коротко о главном

Определение:

Функция, описывающая обратную пропорциональность, – это функция вида \( \displaystyle y=\frac+b \), где \( k\ne 0\), \( x\ne 0\) и \( x\ne а\)

По-другому эту функцию называют обратной зависимостью.

Область определения и область значений функции:

График обратной пропорциональности (зависимости) – гипербола.

Коэффициент \( \displaystyle k\)

\( \displaystyle k\) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).

Знак коэффициента \( \displaystyle k\) влияет на то, в каких четвертях расположен график:

если \( \displaystyle k>0\), то ветви гиперболы расположены в \( \displaystyle I\) и \( \displaystyle III\) четвертях;

если \( \displaystyle k

Коэффициент \( \displaystyle a\)

Если внимательно посмотреть на знаменатель, видим, что \( \displaystyle a\) – это такое число, которому не может равняться \( \displaystyle x\).

То есть \( x=a\) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции

Коэффициент \( b\)

Число \( b\) отвечает за смещение графика функции вверх на величину \( b\), если \( b>0\), и смещение вниз, если \( b

Пример 2

Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).

Напомню, что для этого надо найти корни соответствующего квадратного уравнения: \( \displaystyle <^<2>>+4-5=0\).

Я найду их устно с помощью теоремы Виета: \( \displaystyle <_<1>>=-5\), \( \displaystyle <_<2>>=1\). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения».

Итак, получаем: \( \displaystyle <^<2>>+4-5=\left( x+5 \right)\left( x-1 \right)\), следовательно:

Пример 3

Ты уже попробовал решить сам? В чем загвоздка?

Наверняка в том, что в числителе у нас \( \displaystyle 2x\), а в знаменателе – просто \( \displaystyle x\).

Это не беда. Нам нужно будет сократить на \( \displaystyle \left( x+2 \right)\), поэтому в числителе следует вынести \( \displaystyle 2\) за скобки (чтобы в скобках \( \displaystyle x\) получился уже без коэффициента):

Ответ: \( \displaystyle y=2-\frac<5>\).

График обратной пропорциональности

Как всегда, начнем с самого простого случая: \( \displaystyle y=\frac<1>\).

Таблица обратной пропорциональности (зависимости)

Нарисуем точки на координатной плоскости:

Теперь их надо плавно соединить, но как?

Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.

Это график гиперболы и выглядит он так:

Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.

Каждая из них стремится своими концами приблизиться к осям \( \displaystyle Ox\) и \( \displaystyle Oy\), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:

Оно и понятно: так как \( \displaystyle x\ne 0\), график не может пересекать ось \( \displaystyle Oy\). Но и \( \displaystyle y\ne 0\), так что график никогда не коснется и оси \( \displaystyle Ox\).

Ну что же, теперь посмотрим на что влияют коэффициенты.

На что влияют коэффициенты

Рассмотрим такие функции:

Ух ты, какая красота!

Все графики построены разными цветами, чтобы легче было их друг от друга отличать.

Итак, на что обратим внимание в первую очередь?

Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси \( \displaystyle Ox\).

Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.

А что, если функция выглядит сложнее, например, \( \displaystyle y=\frac<1>+2\)?

В этом случае гипербола будет точно такой же, как обычная \( \displaystyle y=\frac<1>\), только она немного сместится. Давай думать, куда?

Чему теперь не может быть равен \( x\)? Правильно, \( x\ne 1\). Значит, график никогда не достигнет прямой \( x=1\).

А чему не может быть равен \( y\)? Теперь \( y\ne 2\). Значит, теперь график будет стремиться к прямой \( y=2\), но никогда ее не пересечет.

Итак, теперь прямые \( x=1\) и \( y=2\) выполняют ту же роль, которую выполняют координатные оси для функции \( \displaystyle y=\frac<1>\).

Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):

Более подробно о том, как строятся такие графики, мы выучим чуть позже.

А теперь попробуй решить несколько примеров для закрепления.

Примеры

1. На рисунке изображен график функции \( \displaystyle y=\frac\). Определите \( k\).

2. На рисунке изображен график функции \( \displaystyle y=\frac\). Определите \( k\)

3. На рисунке изображен график функции \( \displaystyle y=\frac<1>\). Определите \( a\).

4. На рисунке изображен график функции \( \displaystyle y=\frac<1>+a\). Определите \( a\).

5. На рисунке приведены графики функций \( \displaystyle y=\frac,\text< >y=\frac\) и \( y=\frac\).

Источник