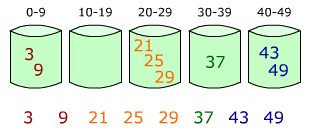Что значит неустойчивая сортировка
Разница между стабильным и нестабильным алгоритмом сортировки?
Недавно в одном из интервью, после некоторых первоначальных вопросов о алгоритмах сортировки, например, как вы пишете QuickSort или разницу между QuickSort и MergeSort, интервьюер спросил, понимаете ли вы разницу между стабильным и нестабильным алгоритмом сортировки? Этот вопрос был новым для моего читателя, поэтому он говорит, извините, никогда не слышал об этом. На этом история закончилась, и Интервьюер перешел к следующему вопросу, но, как и многие из нас, мой читатель продолжил, чтобы узнать больше о оставшихся без ответа вопросах, и в конечном итоге он спросил меня, что означает стабильный и нестабильный алгоритм сортировки? Некоторые из вас могут слышать об этом, и многие из вас могут не знать об этом различии, я постараюсь ответить на этот вопрос в этой статье.
Алгоритм сортировки называется стабильным, если он поддерживает относительный порядок чисел / записей в случае связи, т.е. если вам нужно отсортировать 1 1 2 3, то если вы не измените порядок первых двух, чем ваш алгоритм стабильный, но если поменять их местами, он станет нестабильным, несмотря на то, что общий результат или порядок сортировки останутся прежними
На самом деле, интервьюер может задать этот вопрос в качестве продолжения быстрой сортировки и сортировки слиянием, если вы забудете упомянуть эти понятия. Одно из основных различий между быстрой сортировкой и сортировкой слиянием заключается в том, что ранее она была нестабильной, но сортировка слиянием — это алгоритм устойчивой сортировки.
Стабильный алгоритм против нестабильного
Предположим, вам нужно отсортировать следующие пары ключ-значение в порядке возрастания ключей:
Теперь есть два возможных решения для двух пар, где ключ одинаков, то есть (4,5) и (4,3), как показано ниже:
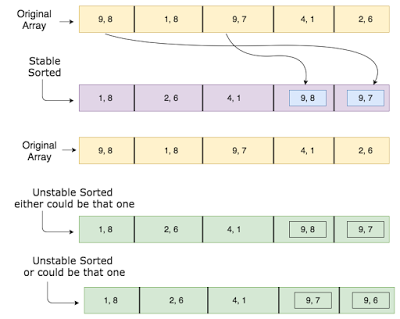
Алгоритм сортировки, который будет производить первый вывод, будет называться стабильным алгоритмом сортировки, поскольку сохраняется исходный порядок равных ключей. Вы можете видеть, что (4, 5) предшествует (4,3) в порядке сортировки, который был исходный порядок, т.е. в данном входе, (4, 5) предшествует (4,3).
С другой стороны, алгоритм, который производит второй вывод, будет известен как нестабильный алгоритм сортировки, поскольку порядок объектов с одинаковым ключом не поддерживается в отсортированном порядке. Вы можете видеть, что во втором выводе (4,3) предшествует (4,5), чего не было в исходном вводе.
Если вы помните, метод Collections.sort () из инфраструктуры Java Collection использует итеративную сортировку слиянием, которая является устойчивым алгоритмом. Это также делает намного меньше сравнения, чем NLog (N) в случае, если входной массив частично отсортирован.
Если вы хотите узнать больше об этой теме, я предлагаю вам прочитать хорошую книгу Томаса Х. Кормена «Структура данных и алгоритмы», например, « Введение в алгоритмы ».
Говорят, что картинка стоит больше 1000 слов, поэтому давайте посмотрим на изображение, которое объясняет, как работает стабильная и нестабильная сортировка:
Дальнейшее чтение
Спасибо за чтение этой статьи. Если вам нравится этот вопрос интервью и мое объяснение, поделитесь с друзьями и коллегами. Если у вас есть какие-либо вопросы или пожелания, оставьте комментарий.
Алгоритмы сортировки данных (Алгоритмы устойчивой сортировки)
Содержание:
Введение
Глава I. Алгоритмы устойчивой сортировки
1.1 Сортировка пузырьком
Сортировка методом пузырька
Теперь подробнее о самом алгоритме. Все достаточно просто :
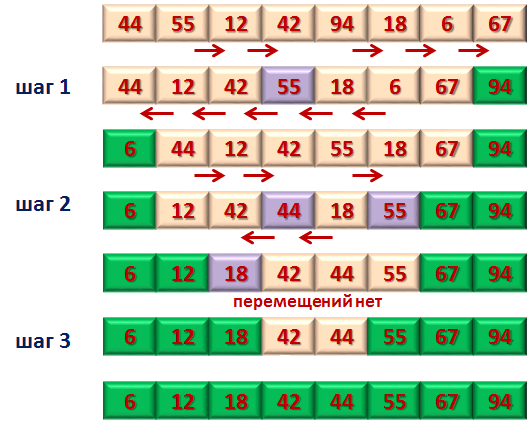
3. Сортировка методом пузырька делится на шаги. В каждом шаге выполняется попарное сравнение. В результате каждого шага наибольшие элементы начинают выстраиваться с конца массива. То есть после первого шага самый большой по значению элемент массива будут стоять на последнем месте. Во втором шаге работа производится со всеми элементами кроме последнего. Опять находится самый большой элемент и ставится в конец массива, с которым производится работа. Третий шаг повторяет второй и так до тех пор, пока массив не будет отсортирован. Для более удобного восприятия приведу наглядный пример. Возьмем массив, состоящий из 7 элементов : 2,5,11,1,7,8,3. Смотрим.(Кликните на картинку для увеличения изображения)
Идея алгоритма очень простая. Идём по массиву чисел и проверяем порядок (следующее число должно быть больше и равно предыдущему), как только наткнулись на нарушение порядка, тут же обмениваем местами элементы, доходим до конца массива, после чего начинаем сначала. Например:
Идём по массиву, проверяем первое число и второе, они идут в порядке возрастания. Далее идёт нарушение порядка, меняем местами эти элементы
Продолжаем идти по массиву, 7 больше 5, а вот 6 меньше, так что обмениваем из местами
3 нарушает порядок, меняем местами с 7
Возвращаемся к началу массива и проделываем то же самое
Это больше похоже на «всплытие» более «лёгких» элементов, как пузырьков, отчего алгоритм и получил такое название.
(см. приложение, Рисунок 1 Пример написания такой сортировки в JavaScript:)
1.2 Шейкер сортировка
Шейкер-сортировка является усовершенствованным методом пузырьковой сортировки.
Анализируя метод пузырьковой сортировки, можно отметить два обстоятельства:
если при движении по части массива перестановки не происходят, то эта часть массива уже отсортирована и, следовательно, ее можно исключить из рассмотрения.
при движении от конца массива к началу минимальный элемент «всплывает» на первую позицию, а максимальный элемент сдвигается только на одну позицию вправо.
Эти две идеи приводят к модификациям в методе пузырьковой сортировки.
От последней перестановки до конца (начала) массива находятся отсортированные элементы. Учитывая данный факт, просмотр осуществляется не до конца (начала) массива, а до конкретной позиции. Границы сортируемой части массива сдвигаются на 1 позицию на каждой итерации.
Массив просматривается поочередно справа налево и слева направо.
Просмотр массива осуществляется до тех пор, пока все элементы не встанут в порядке возрастания (убывания).
Количество просмотров элементов массива определяется моментом упорядочивания его элементов.
Рассмотрим алгоритм Шейкер-сортировки на примере. Дана последовательность
(см. приложение, рисунок 2 Пример)
(См. приложение, Рисунок 3 Пример написания такой сортировки в Pascal)
1.3 Гномья сортировка
Гномья сортировка (англ. Gnome sort) — алгоритм сортировки, который перед вставкой на нужное место происходит серия обменов, как в сортировке пузырьком. Алгоритм находит первое место, где два соседних элемента стоят в неправильном порядке и меняет их местами. Он пользуется тем фактом, что обмен может породить новую пару, стоящую в неправильном порядке, только до или после переставленных элементов. Он не допускает, что элементы после текущей позиции отсортированы, таким образом, нужно только проверить позицию до переставленных элементов. В пример можно отнести причину названия этого способа гномьим. Гномья сортировка основана на технике, используемой обычным голландским садовым гномом (нидерл. tuinkabouter). Это метод, которым садовый гном сортирует линию цветочных горшков. По существу он смотрит на следующий и предыдущий садовые горшки: если они в правильном порядке, он шагает на один горшок вперёд, иначе он меняет их местами и шагает на один горшок назад. Граничные условия: если нет предыдущего горшка, он шагает вперёд; если нет следующего горшка, он закончил.
Незамысловатый обменный алгоритм с неплохой сложностью O(n2), который, как ни парадоксально, совсем недавно был впервые описан в научной литературе.
«Новую сортировку» презентовал на страницах научного издания Newsletter Университета Глазго, некий Хамид Сарбази-Асад (Hamid Sarbazi-Azad) в 2000 году. Он предложил название «Глупая сортировка».
Голландский учёный Дик Грун (Dick Grune) исследовал метод подробнее и переименовал в «Гномью сортировку», под этим именем алгоритм сейчас и известен.
«Гномья сортировка основана на технике, используемой обычным голландским садовым гномом (нидерл. tuinkabouter). Это метод, которым садовый гном сортирует линию цветочных горшков. По существу он смотрит на следующий и предыдущий садовые горшки: если они в правильном порядке, он шагает на один горшок вперёд, иначе он меняет их местами и шагает на один горшок назад. Граничные условия: если нет предыдущего горшка, он шагает вперёд; если нет следующего горшка, он закончил.»
Гномья сортировка это оптимизированная глупая сортировка. В глупой сортировке при нахождении неотсортированной пары соседей происходит обмен и возврат в начало массива. В гномьей сортировке просто делается один шаг назад.
Также алгоритм интересен тем, что используется всего лишь один цикл, что для алгоритмов сортировок большая редкость.
Метод можно ускорить, если запоминать индекс крайнего неотсортированного элемента. После того как сделан ряд шагов назад, дальнейшую обработку массива можно продолжить с того места, где прервались.
Если в оптимизированной гномьей сортировке вместо обменов использовать сдвиг элементов с помощью буферной области памяти, то мы получаем сортировку вставками.
(см. приложение, Рисунок 4 Пример применения такой сортировки в Java)
1.4 Сортировка вставками
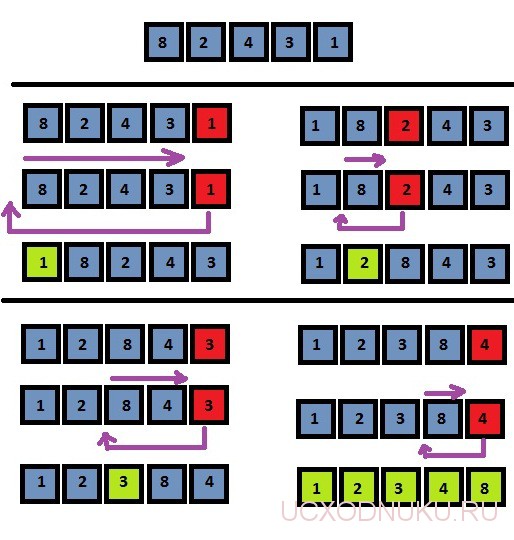
Сортировка вставками — третий и последний из простых алгоритмов сортировки. Сначала он сортирует два первых элемента массива. Затем алгоритм вставляет третий элемент в соответствующую порядку позицию по отношению к первым двум элементам. После этого он вставляет четвертый элемент в список из трех элементов. Этот процесс повторяется до тех пор, пока не будут вставлены все элементы. Например, при сортировке массива dcab каждый проход алгоритма будет выглядеть следующим образом:
Вообще говоря, в худших случаях сортировка вставками настолько же плоха, как и пузырьковая сортировка и сортировка посредством выбора, а в среднем она лишь немного лучше. Тем не менее, у сортировки вставками есть два преимущества. Во-первых, ее поведение естественно. Другими словами, она работает меньше всего, когда массив уже упорядочен, и больше всего, когда массив отсортирован в обратном порядке. Поэтому сортировка вставками — идеальный алгоритм для почти упорядоченных списков. Второе преимущество заключается в том, что данный алгоритм не меняет порядок одинаковых ключей. Это значит, что если список отсортирован по двум ключам, то после сортировки вставками он останется упорядоченным по обоим.
Несмотря на то, что количество сравнений при определенных наборах данных может быть довольно низким, при каждой вставке элемента на свое место массив необходимо сдвигать. Вследствие этого количество перемещений может быть значительным.
Данный алгоритм представляет собой сортировку, в котором элементы входной последовательности просматриваются по одному, и каждый новый поступивший элемент размещается в подходящее место среди ранее упорядоченных элементов.
(см. приложение, рисунок 5 Пример)
(см. приложение, рисунок 6 Пример реализации в Java)
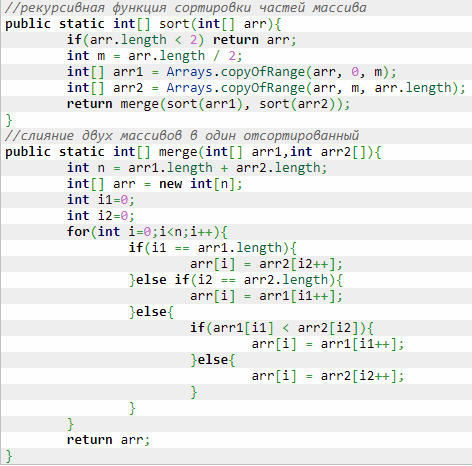
1.5 Сортировка слиянием
Сортировка слиянием (marge sort) — алгоритм сортировки, который упорядочивает списки (или другие структуры данных, доступ к элементам которых можно получать только последовательно, например — потоки) в определённом порядке. Эта сортировка — хороший пример использования принципа «разделяй и властвуй». Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Наконец, их решения комбинируются, и получается решение исходной задачи. (так говорит Википедия).
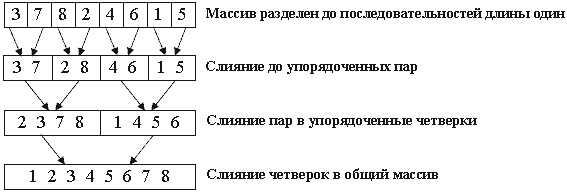
То есть, на входе мы получаем некий массив данных (для простоты и удобства, будем рассматривать целочисленный массив) на n элементов. Затем, делим этот массив на два подмассива размером n/2. И так до тех пор, пока массив не уменьшится до двух элементов, которые достаточно просто отсортировать. Как вы уже могли понять, процедура дробления осуществляется путем рекурсии.
После сравнения двух элементов наш процесс начинает возвращаться и собирать себя по отсортированным кусочкам массива. В процессе обратного слияния элементы подмассивов сравниваются между собой и в окончательный массив вставляется меньший элемент.
Данный способ означает объединение двух (или более) последовательностей в одну упорядоченную последовательность при помощи циклического выбора элементов, доступных в данный момент.
Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Затем их решения комбинируются, и получается решение исходной задачи.
(см. приложение Рисунок 7 Пример)
(см. приложение Рисунок 8 Пример реализации в Java)
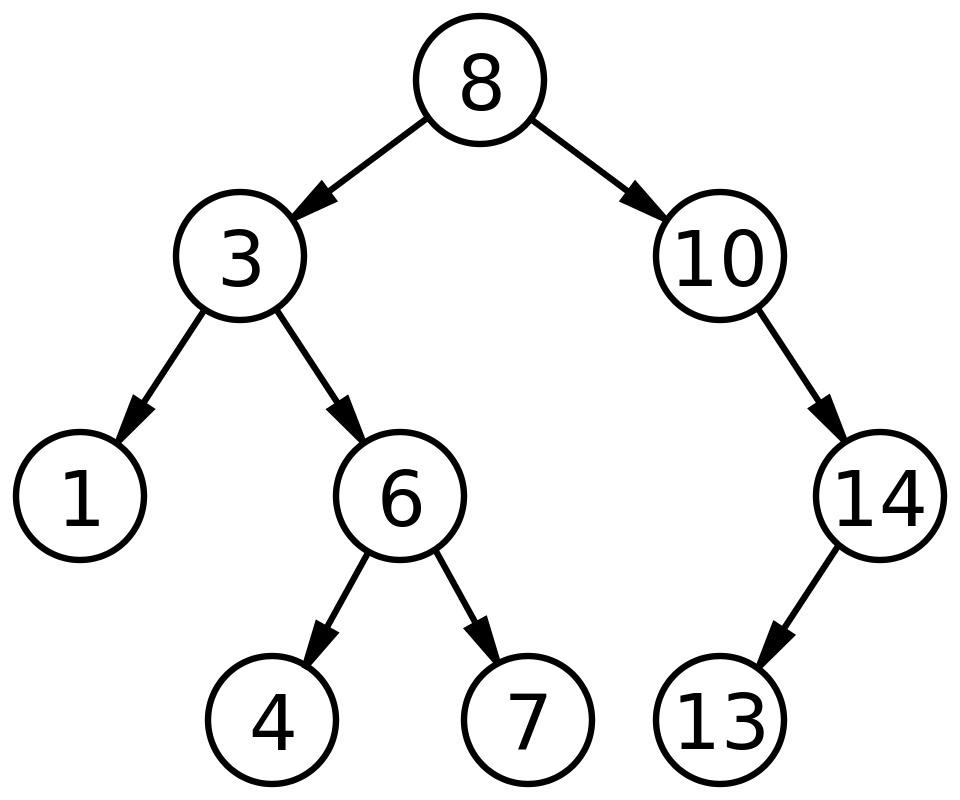
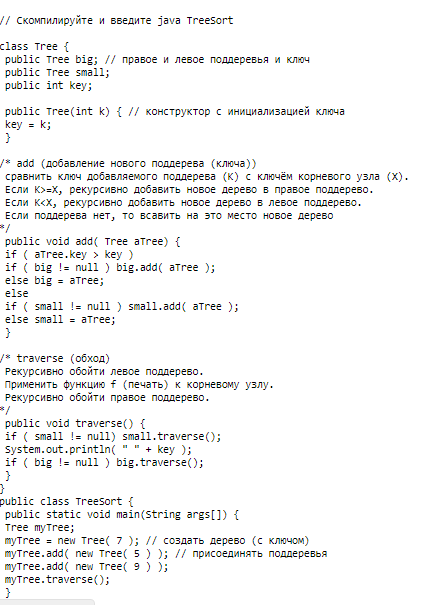
1.6 Сортировка с помощью двоичного дерева
Сортировка с помощью двоичного дерева (сортировка двоичным деревом, сортировка деревом, древесная сортировка, сортировка с помощью бинарного дерева, англ. tree sort) — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения с потока (например с файла, сокета или консоли).
1. Построение двоичного дерева.
2. Сборка результирующего массива путём обхода узлов в необходимом порядке следования ключей.
Процедура добавления объекта в бинарное дерево имеет среднюю алгоритмическую сложность порядка O(log(n)). Соответственно, для n объектов сложность будет составлять O(n log(n)), что относит сортировку с помощью двоичного дерева к группе «быстрых сортировок». Однако, сложность добавления объекта в разбалансированное дерево может достигать O(n), что может привести к общей сложности порядка O(n²).
При физическом развёртывании древовидной структуры в памяти требуется не менее чем 4n ячеек дополнительной памяти (каждый узел должен содержать ссылки на элемент исходного массива, на родительский элемент, на левый и правый лист), однако, существуют способы уменьшить требуемую дополнительную память.
Двоичным(бинарным) деревом назовем упорядоченную структуру данных,
поставлены в соответствие по крайней мере два других элемента (преемника).
Причем для каждого предшественника выполнено следующее правило:
левый преемник всегда меньше, а правый преемник всегда больше или равен
Вместо ‘предшественник’ и ‘преемник’ также употребляют термины
‘родитель’ и ‘сын’. Все элементы дерева также называют ‘узлами’.
При добавлении в дерево нового элемента его последовательно сравнивают
с нижестоящими узлами, таким образом вставляя на место.
и так далее, пока есть сыновья, с которыми можно сравнить
Представляет собой универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения с потока (например из файла, сокета или консоли).
(см. приложение Рисунок 9 Пример)
(см. приложение Рисунок 10 Реализация в Java)
1.7 Сортировка подсчетом
Это сортировка может использоваться только для дискретных данных. Допустим, у нас
есть числа от 0 до 99, которые нам следует отсортировать. Заведем массив размером в 100
элементов, в котором будем запоминать, сколько раз встречалось каждое число (т.е. при
появлении числа будем увеличивать элемент вспомогательного массива с индексом, равным
этому числу, на 1). Затем просто пройдем по всем числам от 0 до 99 и выведем каждое
столько раз, сколько оно встречалось. Сортировка реализуется следующим образом:
for (i=0; i 2) вспомогательных файлов.
Общий алгоритм сортировки слиянием
Сначала серии распределяются на два или более вспомогательных файлов. Данное распределение идет поочередно: первая серия записывается в первый вспомогательный файл, вторая – во второй и так далее до последнего вспомогательного файла. Затем опять запись серии начинается в первый вспомогательный файл. После распределения всех серий, они объединяются в более длинные упорядоченные отрезки, то есть из каждого вспомогательного файла берется по одной серии, которые сливаются. Если в каком-то файле серия заканчивается, то переход к следующей серии не осуществляется. В зависимости от вида сортировки сформированная более длинная упорядоченная серия записывается либо в исходный файл, либо в один из вспомогательных файлов. После того как все серии из всех вспомогательных файлов объединены в новые серии, потом опять начинается их распределение. И так до тех пор, пока все данные не будут отсортированы.
Выделим основные характеристики сортировки слиянием:
количество фаз в реализации сортировки;
количество вспомогательных файлов, на которые распределяются серии.
3.3. Блинная сортировка
Непрактичность ее состоит в том, что в данном алгоритме вообще не учитывается количество сравнений элементов (считается, что эти операции очень дешевы и быстры), а единственной операцией, имеющей цену, является переворот верхушки стопки сортируемых «блинов». Разумеется, изначально они расположены в произвольном порядке, а желаемым результатом является некое подобие ханойской башни, когда блины большего диаметра лежат снизу, а меньшего располагаются сверху.
По поводу этой задачи хочется отметить два интересных факта. Во-первых, способ нахождения достаточно эффективного (хотя и неоптимального) решения был в свое время предложен небезызвестным Биллом Гейтсом, пока тот был еще студентом. Этот алгоритм, предложенный в 1979 году, оставался наиболее эффективным вплоть до 2008, когда результат был превзойден. Во-вторых, как было доказано впоследствии, задача нахождения оптимального решения относится к классу NP-полных. Также Гейтсом и его руководителем Христосом Пападимитриу был предложен усложненный вариант задачи, известный как задача о подгоревших блинах.
Задача о подгоревших блинах
В этой форме задачи каждый элемент, помимо размера, имеет еще и бинарный атрибут «направление», то есть у каждого «блина» одна сторона подгоревшая, а другая румяная; результатом решения задачи является стопка, упорядоченная по размеру, но, помимо этого, все «блины» лежат подгоревшей стороной вниз. Не вдаваясь в подробности, скажем, что и эта задача NP-полна, и что в общем случае известны ее достаточно эффективные, но неоптимальные решения. Тем не менее, существуют ограничения на данные, при выполнении которых задача становится полиномиальной. Для рассматриваемой задачи такими данными являются простые перестановки. Чтобы понять, что это такое, рассмотрим перестановку чисел от 1 до 7: 2647513. Заметим, что выделенная жирным шрифтом последовательность сама является перестановкой чисел от 4 до 7 (называется блоком). Простые перестановки — это те, где нет нетривиальных блоков (блоков длины 1 и n).
За образной постановкой задачи, когда элементы представлены подгоревшими блинами, сложно разглядеть тот факт, что она имеет биологическое значение. Тем не менее, распространенной мутацией является переворот в молекуле ДНК, и если посчитать минимальное количество переворотов, необходимое для преобразования одной молекулы в другую (без рассмотрения более мелких точечных мутаций), то можно примерно оценить родство организмов. Например, геном человека и мыши разделен всего лишь порядка 120 глобальными мутациями; признаюсь, я раньше полагал, что между этими видами разницы гораздо больше…
Генетический алгоритм решения задачи о подгоревших блинах
В сравнительной геномике алгоритм используется для аналитического нахождения количества мутаций, разделяющих организмы, но посмотрим на задачу в другой проекции. Теперь уже решение аналитической задачи объявим целью, а живые организмы и процессы, в них протекающие, сделаем инструментом для ее решения.
Как известно, бактерии в состоянии делиться обеспечивая экспоненциальный рост популяции, если им предоставлены необходимые условия; разумеется, через некоторое время колонии бактерий уже не будет хватать питательной среды, также появятся другие факторы, влияющие на рост колонии, но на это необходимо время. Экспериментальным путем мы можем выяснить среднее время, которое требуется бактериям данного вида на появление глобальной мутации, связанной с переворотом части ДНК.
Теперь поставим бактериям задачу. Генетически модифицируем одну из них (биологи любят в подобных экспериментах использовать кишечную палочку), где ген устойчивости к антибиотику разобьем на несколько частей и перемешаем между собой, меняя при этом не только порядок, но и направление некоторых кусков. Таким образом, каждый перевернутый и переставленный кусок гена в нашем случае будет представлять собой «подгоревший блин».
Задача бактерии поставлена, можно начинать эксперимент. Помещаем ее в питательную среду и ждем отведенное время, за которое ожидается появление одной мутации-переворота ДНК. Обращаю внимание на то, что мы считаем одной мутацией: она единственна не на всю колонию (как раз в колонии этих мутаций будет много); это всего лишь ожидаемое количество переворотов у каждой из ныне живущих бактерий по сравнению с их прародителем.
Достаточно ли одного переворота блина для решения задачи? Мы легко это можем проверить, поместив часть колонии в опасную для нее среду. Помещенные в антибиотик бактерии не выжили, и мы продолжаем наблюдать за оставшимися. Пройдет еще два-три периода, и, наконец, в группе бактерий, помещенных в антибиотик, останутся живые. «Коллективный разум» справился с задачей!
Конечно, полезность решенной задачи нас вряд ли впечатлит: в реальных проведенных экспериментах количество сортируемых «блинов» не превышает четырех, а количество мутаций, происходящее за отведенное время, может быть оценено лишь вероятностно. И все же лично меня поразила фантазия тех биологов, которые смогли поставить эксперимент; не меньшей фантазией обладали и те, кто смог биологическим методом решить задачу коммивояжера (подробности этого эксперимента я оставлю за рамками данной статьи). Во многом сложность задач, решаемых генетическими алгоритмами, сравнима с квантовыми вычислениями, и хочется верить, что оба направления неклассических вычислений смогут дать результаты пока не достижимые в современных условиях.
Заключение
Сортировка применяется во всех без исключения областях программирования, будь то базы данных или математические программы. Алгоритмы сортировки представляют собой пошаговое упорядочение элементов в определенном массиве данных, независимо от его размеров.
Практически каждый алгоритм сортировки можно разбить на три части:
— сравнение, определяющее упорядоченность пары элементов;
— перестановку, меняющую местами пару элементов;
— собственно сортирующий алгоритм, который осуществляет сравнение и перестановку элементов до тех пор, пока все элементы множества не будут упорядочены.
Выбор метода сортировки в значительной мере зависит от объема и характеристики исходных данных. Но, в целом, основными параметрами, которыми руководствуется пользователь при выборе метода сортировки, являются время действия алгоритма, память, устойчивость сортировки и эффективность поведения алгоритма.
Наиболее известными и, одновременно, базовыми алгоритмами сортировки являются обменная, блочная, пирамидальная, линейная, быстрая сортировки, а также сортировки подсчетом, слиянием, перемешиванием и методом вставок. Каждый из этих методов имеет свои достоинства и недостатки.
Термин «алгоритм» применяют весьма широко. Алгоритм – это организованная последовательность действий, допустимых в определенных случаях. Умение разбить задачу на подзадачи, распределение решений этих задач, определение выходных параметров способствуют легкому восприятию любой ситуации.
Список использованной литературы
Приложение 1 Пример написания такой сортировки в JavaScript:
Приложение 2 Пример
Приложение 3 Пример написания такой сортировки в Pascal
Приложение 4 Пример применения такой сортировки в Java
Приложение 5 Пример
Приложение 6 Пример реализации в Java
Приложение 7 Пример
Приложение 8 Пример реализации в Java
Приложение 9 Пример
Приложение 10 Реализация в Java
Приложение 11 Реализация в Java
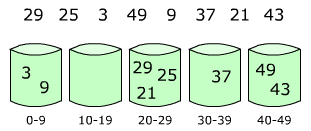
Приложение 12 Элементы распределяются по корзинам
Приложение 13 Затем элементы в каждой корзине сортируются
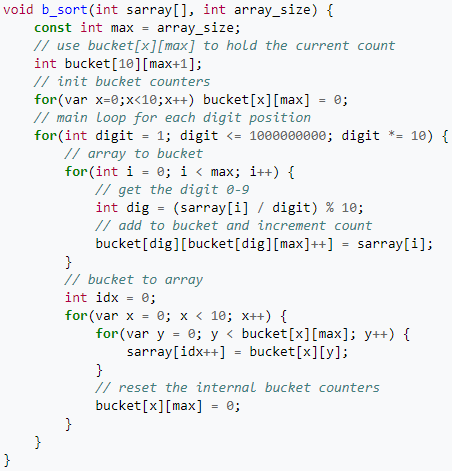
Приложение 14 Реализация в C
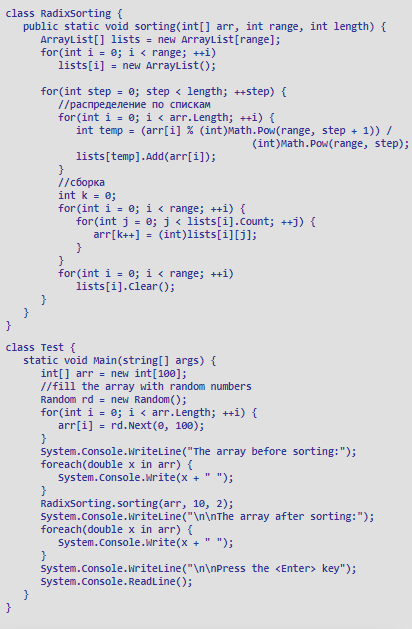
Приложение 15 Реализация в С#
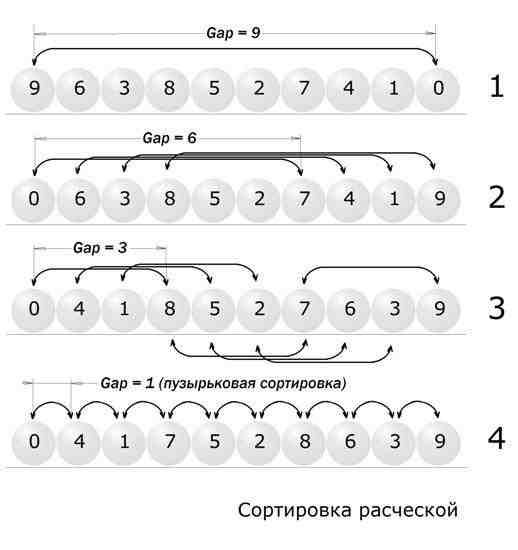
Приложение 16 Пример сортировки расческой
Приложение 17 Реализация в C#
Приложение 18 Реализация в C
Приложение 19 Пример, часть 1
Приложение 20 Пример, часть 2
Приложение 21. Реализация в C
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.