Что значит несовместные события в теории вероятности
1.2.2. Совместные и несовместные события.
Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
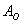
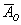
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
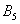
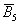
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
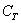
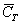
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, 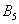
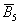
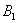
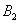
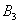
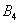
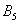
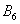
События 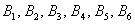
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 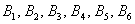
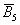
В примере с картами события 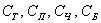
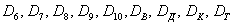
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
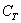
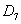
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
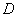
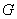
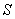
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №34. Условная вероятность. Независимость событий.
Перечень вопросов, рассматриваемых в теме:
— Совместные и несовместные события
— Схема решения задач на вычисление условной вероятности события;
— Задачи на определение независимости событий.
Совместные события – события, одновременное появление которых возможно.
Несовместные события – события, одновременное появление которых невозможно.
События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.
Событие В называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается PA(B).
Условная вероятность – вероятность наступления одного события при условии, что другое событие уже произошло.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. с. 186-194.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Иногда нам требуется выяснить вероятность совместного появления зависимых событий. Самый простой пример – найти вероятность получить выигрышную комбинацию в азартной карточной игре, где вероятность выпадения каждой новой карты зависит от того, какие карты уже лежат на столе.
Рассмотрим примерную задачу:
Из колоды карт извлекают четыре карты. Первые две оказались семёрками. Какова вероятность, что одна или обе оставшиеся карты окажутся семёрками? (колода содержит 36 карт)
События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Пример совместных событий: выпадение чётного числа и выпадение числа, кратного трём, при броске игрального кубика. Когда выпадает шесть, реализуются сразу оба события.
События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.
Пример несовместных событий: выпадение чётного числа и выпадение нечётного числа при броске игрального кубика.
Теорема о сумме двух событий:
Вероятность суммы любых двух событий А и В равна сумме вероятностей этих событий без вероятности их совместного осуществления: Р(А+В) = Р(А)+Р(В)-Р(АВ)
В лотерее выпущено 10 000 билетов, из них: 10 выигрышей по 200 рублей, 100 выигрышей по 100 рублей, 500 выигрышей по 50 рублей и 1000 выигрышей по 10 рублей. Какова вероятность того, что человек, купивший билет, выиграет не менее 50 рублей?
Воспользуемся теоремой: Р(М)=Р(А)+Р(В)+Р(С)=0,061.
Дана вероятность исходного события. Чему равна вероятность противоположного события?
Вероятность исходного события А обозначим Р(А). Вероятность противоположного события Р(Ᾱ).
События А и Ᾱ образуют полную группу событий, вероятность которой равна 1.
Тогда вероятность противоположного события находится по формуле:
Например, монета брошена два раза.
Вероятность появления «Орла» во втором испытании не зависит от результата первого испытания.
Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий A и B равна произведению вероятностей этих событий:
Подбрасываются две монеты. Найдите вероятность выпадения двух орлов.
Введем обозначение событий:
A1– на 1-й монете выпадет орёл;
A2– на 2-й монете выпадет орёл.
Событие “выпадение двух орлов” заключается в том, что на 1-й монете появится орёл и на 2-й монете появится орёл, следовательно, это произведение событий A1A2. Вероятность выпадения орла на одной монете не зависит от результата броска другой монеты, следовательно, события A1 и A2 независимы. По теореме умножения вероятностей независимых событий получим:
Отыскать вероятность совместного появления зависимых событий помогает теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло: P(AB) = P(A)·PA(B).
Связь теории вероятностей с теорией множеств.
В математике принято устанавливать связи между различными разделами. Связь между теорией вероятностей и теорией множеств устанавливается следующим образом: события отождествляются с множествами. В таком случае понятию исход будет эквивалентно понятие элемент множества. При таком подходе выберите из списка, какому понятию из теории множеств соответствует данное понятие из теории вероятностей:
— Невозможное событие (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
— Сумма событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
— Произведение событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
Примеры и разбор решения заданий тренировочного модуля
1. В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара без возврата. Найдите вероятность того, что первый шар окажется черным, второй – красным и третий – белым.
А – первый шар окажется черным

2. Колю отпускают гулять при условии сделанных уроков с вероятностью 0,8. Папа выдает ему деньги на мороженое с вероятностью 0,6. С какой вероятностью Коля пойдет гулять без мороженого?
A – папа выдал Коле денег на мороженое
B – Колю отпустили гулять
Вероятность того, что Коля пойдёт гулять, есть в условии задачи P(B) = 0,8. Вероятность, что папа не выдаст ему деньги на мороженое, равна P(Ᾱ) = 1 – P(A) = 1 – 0,6 = 0,4. Вероятность одновременного осуществления двух независимых событий – произведение их вероятностей P(ᾹB) = P(Ᾱ)·P(B) = 0,8·0,4 = 0,32.
Теория вероятности. Часть 2
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.
Подборку задач на отработку темы смотрите здесь.
Теория вероятности. Часть 2
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.
Подборку задач на отработку темы смотрите здесь.

