Что значит неположительное число
Целые числа
Вы будете перенаправлены на Автор24
Что значит целое число
Итак, рассмотрим, какие числа называют целыми.
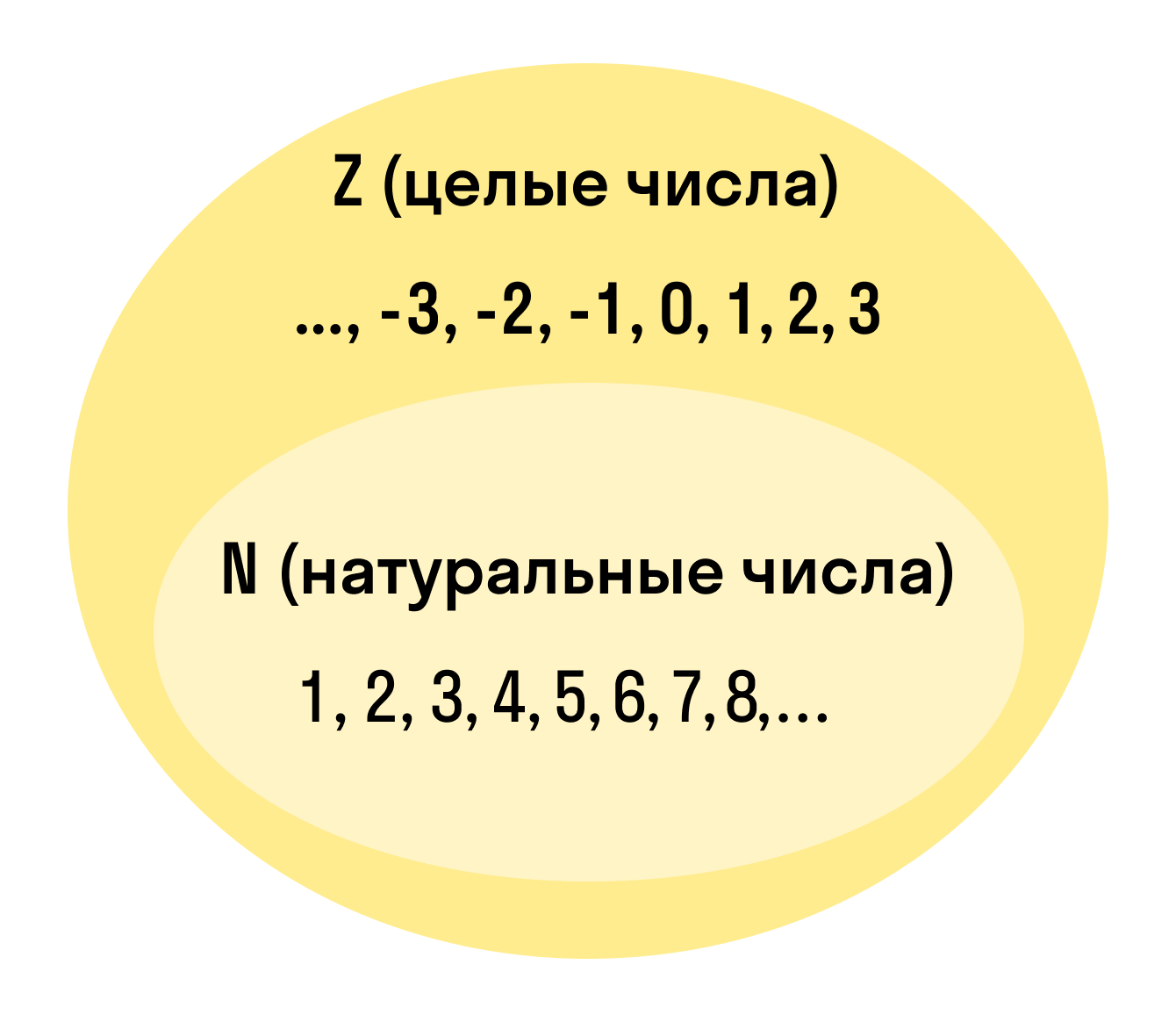
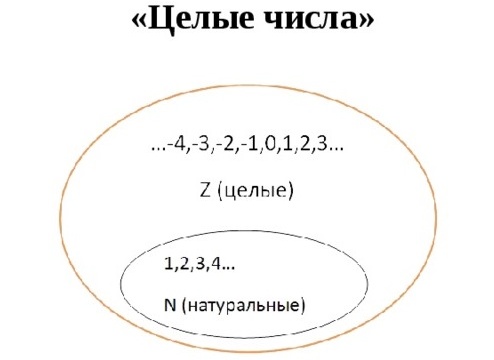
Если вспомнить курс математики, то целыми числами являются натуральные числа, нуль и числа, противоположные натуральным.
Множество натуральных чисел есть подмножеством множества целых чисел, т.е. любое натуральное будет являться целым числом, но не любое целое является натуральным числом.
Целые положительные и целые отрицательные числа
Целыми положительными числами являются целые числа со знаком плюс.
Целыми отрицательными числами являются целые числа со знаком минус.
Число ноль не относится ни к целым положительным, ни к целым отрицательным числам.
Целыми положительными числами являются целые числа, большие нуля.
Целыми отрицательными числами являются целые числа, меньшие нуля.
Множество натуральных целых чисел являет собой множество всех целых положительных чисел, а множество всех противоположных натуральным числам являет собой множество всех целых отрицательных чисел.
Целые неположительные и целые неотрицательные числа
Все целые положительные числа и число нуль называются целыми неотрицательными числами.
Готовые работы на аналогичную тему
Таким образом, целым неотрицательным числом являются целые числа, большие нуля или равные нулю, а целым неположительным числом – целые числа, меньшие нуля или равные нулю.
Описание изменения величин при помощи целых чисел
Целые числа применяются для описания изменения числа каких-либо предметов.
Целые числа удобно использовать, т.к. не нужно явное указание на увеличение числа или уменьшение, – знак целого числа указывает на направление изменения, а значение – на количественное изменение.
С помощью целых чисел можно выразить не только изменение количества, но и изменение любой величины.
Рассмотрим пример изменения стоимости товара.
Отдельно рассмотрим значение отрицательных целых чисел как размера долга.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 08 06 2021
Какие числа называются целыми
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение целых чисел
Что важно знать о целых числах:
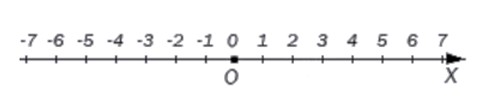
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Урок 27 Бесплатно Координаты на прямой
В этом уроке мы познакомимся с положительными и отрицательными числами, поймем, к чему относится нуль.
Не забудем рассказать также про неположительные и неотрицательные числа, а после этого узнаем, что такое координатная прямая и из чего она состоит.
Положительные и отрицательные числа
Начнем с сухих, но емких определений.
Обычно + не пишется, а просто подразумевается.
Мы могли бы их записать и со знаком «+»:
В таком случае нужно читать запись буквально: «плюс два», «плюс одна вторая» и так далее.
Такая запись добавляет громоздкости записи, и обычно все- таки «+» опускают.
Приведем примеры отрицательных чисел:
-3, \(\mathbf<-\frac<1><6>>\), \(\mathbf<-32\frac<4><5>>\), -784285332
Читать в данном случае также нужно дословно: «минус три», «минус одна шестая» и так далее.
Минус уже опустить нельзя, так как тогда получится, что число положительное.
Важные факты:
Если нам надо сравнить два числа, одно из которых положительное, а другое отрицательное, то можно смело утверждать, что число, которое положительно, больше числа, которое отрицательно.
Если надо сравнить число с нулем, то достаточно понять, положительное оно или отрицательное. Если положительное, значит, больше нуля, если же отрицательное, то меньше нуля.
Более подробно про сравнение чисел мы поговорим в следующих уроках, а пока потренируемся отличать положительные и отрицательные числа.
Пройти тест и получить оценку можно после входа или регистрации
Неположительные и неотрицательные числа
Иногда необходимо обозначить множество чисел, больших или равных нулю, или же наоборот, меньших или равных нулю.
Удобно, что для этого есть специальные определения.
Соответственно, если мы хотим привести примеры неотрицательных чисел, то можем привести положительные числа или 0.
Примеры: 0, 1, 956, \(\mathbf<\frac<4><9>>\), \(\mathbf<342\frac<1><9>>\).
В данном случае примерами будут соответственно отрицательные числа или 0.
Если необходимо определить, является ли число неотрицательным или неположительным, то ответить надо следующим образом:
Также отметим важные факты про сравнение неположительных и неотрицательных чисел с нулем:
Пройти тест и получить оценку можно после входа или регистрации
Координатная прямая
Начнем с определения, а потом посмотрим на вариации и примеры координатных прямых в жизни.
Если хотя бы одной из этих трех составляющих нет, то прямая уже не может быть координатной.
Выше мы показали самую простую вариацию координатной прямой.
Но обычно для удобства наносят штрихи по всей длине, чтобы не отмерять единичные отрезки.
Также мы можем подписывать числа не только под точкой начала отсчета и точкой, дающей понимание о длине единичного отрезка, но и под остальными точками тоже.
Если мы не хотим загромождать картинку, то можно отмечать точки с какой-то периодичностью.
Неизменным на всех этих картинках остается наличие трех пунктов из определения:
В жизни координатные прямые, полностью удовлетворяющие нашему определению, могут встречаться довольно редко.
Например, на ртутном термометре подразумевается, что направление совпадает с направлением увеличения чисел на шкале.
На нем же мы видим, что числа стоят не у каждого штриха, а у каждого 5-го или каждого 10-го, так картинка становится более читаемой.
Еще один пример: обычная линейка или рулетка. Тут тоже направление подразумевается, поэтому нельзя однозначно сказать, что это координатная прямая.
На линейке, в отличие от градусника, не часто увидишь отрицательные числа. Действительно, -5 градусов интересуют нас больше, чем -5 сантиметров.
На этом рисунке видно, что у точки начала координат (точка O) координата равна нулю, а у точки (А), дающей информацию о единичном отрезке,
координата- 1.
Чтобы найти координату точки мы должны отсчитать количество единичных отрезков между точкой и точкой начало отсчета. А дальше, если эта точка стоит после точки начала отсчета, то взять количество единичных отрезков. В противном случае, если точка находится перед точкой начала отсчета, то взять количество единичных отрезков со знаком «минус».
Например, чтобы найти координату точки C мы отсчитываем количество отрезков от начала координат; получаем, что их 2, запоминаем это.
Точка С находится справа от точки начала отсчета, или дальше по направлению, чем точка начала отсчета. Значит, берем непосредственно число 2 в качестве координаты.
Между точкой B и точкой начала отсчета 3 единичных отрезка, но если смотреть относительно точки начала отсчета, то она находится левее или раньше по направлению, значит, мы берем количество единичных отрезков со знаком «минус» и координатой точки B будет \(\mathbf<-3>\).
Естественно, единичных отрезков между точкой и точкой начала отрезков может получиться нецелое число.
Точка D идет перед точкой начала отсчета, если смотреть по направлению, а значит, координата должна быть отрицательный.
Таким образом, координата точки D будет равна \(\mathbf<-1.5>\).
Мы не случайно отходим от простых понятий «справа»/«слева», когда говорим о взаимном расположении точек.
Представьте, что направление идет в другую сторону.
Ну и конечно же, прямая может быть вообще расположена вертикально, тогда говорить о направлениях «право»/«лево» вообще не приходится.
Пройти тест и получить оценку можно после входа или регистрации
Целые числа
Что такое целые числа
Целые числа — это множество натуральных чисел, отрицательных и нуль.
Другими словами определение можно сформулировать так: целые числа — такие, у которых нет дробной части. Любое натуральное число считается целым, но не любое целое является натуральным.
-98; 24; 0; 3; 4512 — это все целые числа.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Целые числа имеют обозначение в виде знака Z (от нем. названия Zahlen — «числа»). Им присущи три базовые арифметические операции:
А также можно провести специфическую операцию — деление с остатком.
Использование целых чисел при описании изменения величин
Изменение величин каких-либо предметов или объектов удобнее всего описывать с помощью целых чисел. Именно они со своими знаками «+» или «-» наглядно показывают увеличение/уменьшение величины или же ее неизменность, если использовать 0. В этом выражении заключается одно из главных отличий множества целых чисел от натуральных.
Для наглядности можно привести пример, который покажет, как вычислить изменение величин:
На полке хранилось некое количество книг. Затем к ним поставили 10 новых экземпляров. Параметр 10 означает изменение (увеличение, «+») количества предметов. Если с полки потом уберут 5 книг, то этот показатель тоже будет выражать изменение количества предметов, но уже в сторону уменьшения (значение знака «-»).
Если же на полку не поставят новые книги и не заберут старые, то число 0 окажется индикатором неизменности количества предметов.
Кроме того, понятие о целых числах используется не только в алгебре, но и в таких областях, как география, история, медицина, физика.
Положительные и отрицательные целые числа
Положительные целые числа — это числа, которые отмечаются знаком «плюс». К примеру, к ним относятся: 1; 2; 3; 4.
Свойство нуля состоит в том, что он не принадлежит ни к положительным, ни к отрицательным. Оно их разделяет.
Для любого положительного целого числа существует единственное противоположное отрицательное. Справедливо и обратное правило. 0 противоположен самому себе.
Неположительные и неотрицательные целые числа
Неотрицательные целые числа — это положительные целые числа и нуль. К ним можно отнести числа типа 54; 146; 0.
По другому, неположительными целыми числами считают те, которые меньше или равны нулю. И наоборот, неотрицательные те, которые больше или равны нулю.
Данные термины ввели для удобства изъяснения. Для того, чтобы не говорить, что число n — меньше или равно нулю, можно сократить фразу и сказать: число n — целое неположительное.
Целые числа: общее представление
В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.
Целые числа. Определение, примеры
Определение 1. Целые числа
Целые числа и координатная прямая
Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.
В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.
Положительные и отрицательные целые числа
Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.
Определение 2. Положительные целые числа
Определение 3. Отрицательные целые числа
Число 0 разделяет положительные и отрицательные целые числа и само не является ни положительным, ни отрицательным.
Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число.
Можно дать другие формулировки определений отрицательных и положительных целых чисел, используя их сравнение с нулем.
Определение 4. Положительные целые числа
Соответственно, положительные числа лежат правее начала отсчета на координатной прямой, а отрицательные целые числа находятся левее от нуля.
Неположительные и неотрицательные целые числа
Определение 6. Неотрицательные целые числа
Как видим, число нуль не является ни положительным, ни отрицательным.
Использование целых чисел при описании изменения величин
Для чего используются целые числа? В первую очередь, с их помощью удобно описывать и определять изменение количества каких-либо предметов. Приведем пример.
Пусть на складе хранится какое-то количество коленвалов. Если на склад привезут еще 500 коленвалов, то их количество увеличится. Число 500 как раз и выражает изменение (увеличение) количества деталей. Если потом со склада увезут 200 деталей, то это число также будет характеризовать изменение количества коленвалов. На этот раз, в сторону уменьшения.
Если же со склада ничего не будут забирать, и ничего не будут привозить, то число 0 укажет на неизменность количества деталей.
Очевидное удобство использования целых чисел в отличие от натуральных в том, что их знак явно указывает на направление изменения величины (увеличение или убывание).