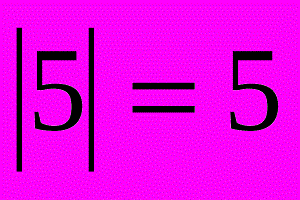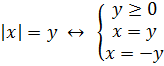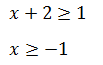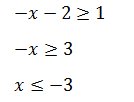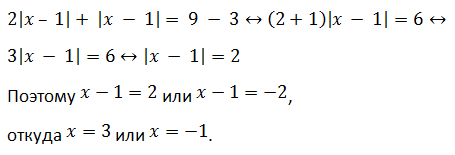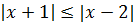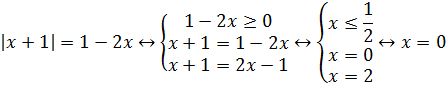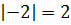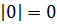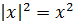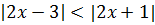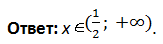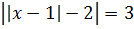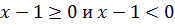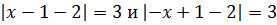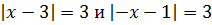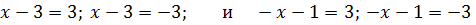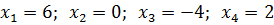Что значит не превышает в математике

Игры для быстрого запоминания знаков «больше» и «меньше»

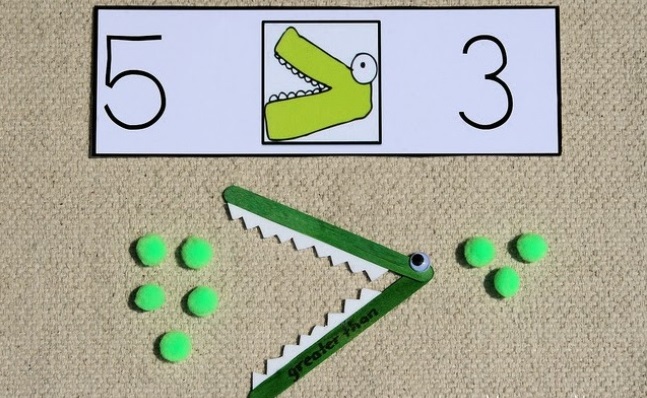
Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и « Игра «Большой голодный крокодил»

Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.

На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и « Игра «Что больше?»

В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа « ». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.

В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.

Игра «Кубики и доски»

Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.

Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».

С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».

Заключение

Источник

Равенство и неравенство. Знаки: больше, меньше, равно

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Математические знаки

Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.

Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:

Символ меньше (

Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:

Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:

Равенство и неравенство

Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.

Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».

Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.

Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:

Типы неравенств

Источник

Знаки больше меньше в какую сторону. Знаки больше и меньше на клавиатуре

Математические знаки

Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.

Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:

Символ меньше ( Как и в какую сторону пишется знак больше

Знак «больше» пишется так «>». Символ обозначается стрелкой, направление острого угла которой обращено в правую сторону. Немного теории: определяющим фактором является левая сторона символа. Если стрелка начинается с двух линий, которые в правой части сходятся в одну точку, тогда это знак «>».

В общем и целом логика понимания очень проста – какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону – такой и знак. Соответственно, знак больше влево смотрит широкой стороной – большей.

Пример использования знака больше:

Как и в какую сторону пишется знак меньше

Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.

Пример использования знака меньше:

100 =», что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.

На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше.

Знак «меньше» выглядит так « Знаки больше и меньше на клавиатуре

Символы больше (>) и меньше ( 2
5 Знаки «больше или равно» / «меньше или равно»

Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или « Читайте также: 10 советов о том, как быстро научить ребёнка говорить

Данные знаки используются в нестрогих неравенствах. В первом классе такие неравенства обычно не изучают.

Игры для быстрого запоминания знаков «больше» и «меньше»

Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и « Игра «Большой голодный крокодил»

Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.

На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и « Игра «Что больше?»

В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа « ». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.

В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.

Игра «Кубики и доски»

Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.

Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».

С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».

Равенство и неравенство

Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.

Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».

Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.

Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:

Источник

Модуль числа знак, свойства, действия, как найти, примеры графиков

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

Модуль комплексного числа

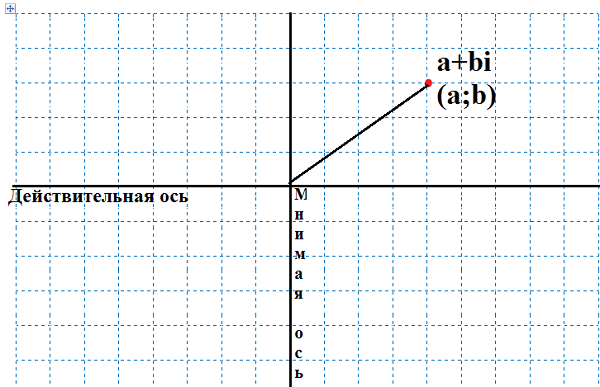
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.

Разделим интервал на 2 части:

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x1 = 3, x2 = − 1.

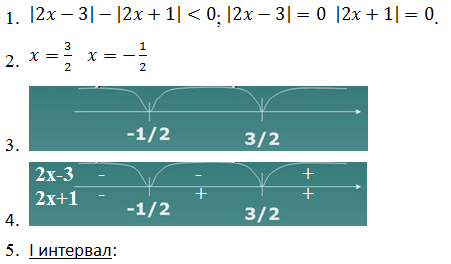
Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Ответ: x = 0.

Модуль суммы

Модуль разности

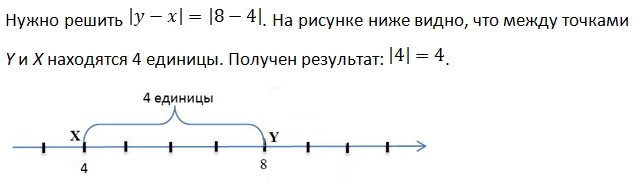
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

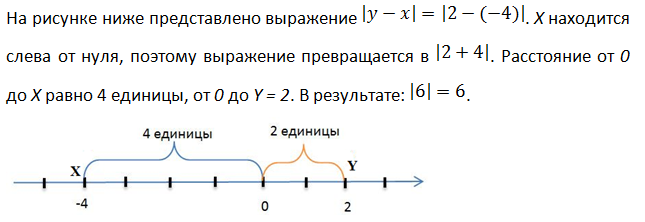
Пример 1.

Пример 2.

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

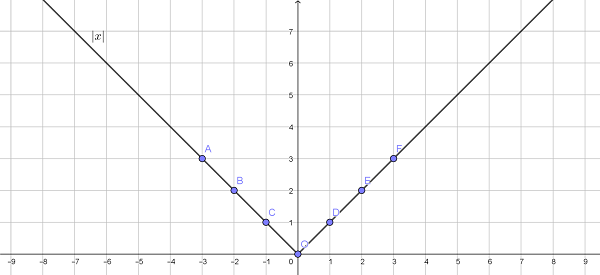
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

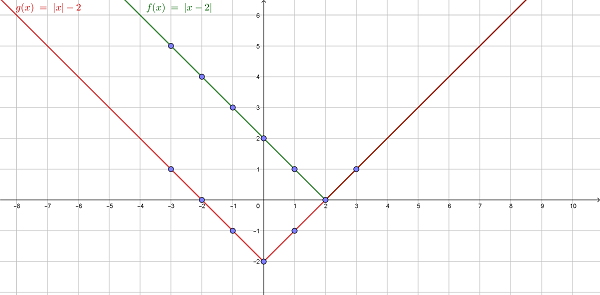
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

Пример 1. Решить методом интервалов.

Решение:

Результатом будет сумма всех подходящих интервалов.

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:

Далее каждое из равенств разделяется еще на два:

Получено четыре результата:

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

Источник

не превышать

Смотреть что такое «не превышать» в других словарях:

превышать — См. превосходить. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. превышать превосходить, перекрывать, переходить, переваливать; побеждать, преобладать … Словарь синонимов

ПРЕВЫШАТЬ — ПРЕВЫШАТЬ, превысить что, быть выше; | что, кого, превосходить, превзойти. Колокольня Иван Великий превышает, или превышает собою, все московские колокольни. Этот корабль величиною превышает все корабли, или величина его превышает размеры иных… … Толковый словарь Даля

ПРЕВЫШАТЬ — ПРЕВЫШАТЬ, превышаю, превышаешь (книжн.). несовер. к превысить. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

превышать — ПРЕВШЫСИТЬ, Шышу, Шысишь; Шышенный; сов. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

превышать по производительности — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN outproduce … Справочник технического переводчика

превышать — превысить объем • много, Neg, оценка, соответствие превысить число • много, Neg, оценка, соответствие превышать возможности • много, Neg, оценка, соответствие превышать длину • много, Neg, оценка, соответствие превышать допустимую норму • много,… … Глагольной сочетаемости непредметных имён

Превышать — несов. перех. 1. Быть выше кого либо по росту, по высоте. 2. Быть больше какого либо числа, количества. 3. Быть больше чего либо (по силе, размерам и т.п.). отт. Выходить за установленные или общепринятые нормы, границы. 4. разг. Обнаруживать… … Современный толковый словарь русского языка Ефремовой

превышать — превыш ать, аю, ает … Русский орфографический словарь

превышать — (I), превыша/ю, ша/ешь, ша/ют … Орфографический словарь русского языка

превышать — Syn: превосходить, перекрывать, переходить, переваливать … Тезаурус русской деловой лексики

превышать — см. превысить; а/ю, а/ешь; нсв … Словарь многих выражений

Источник