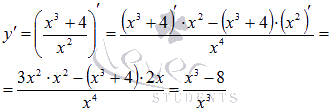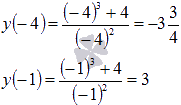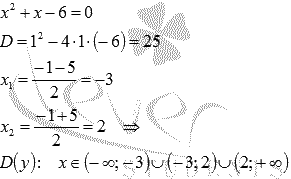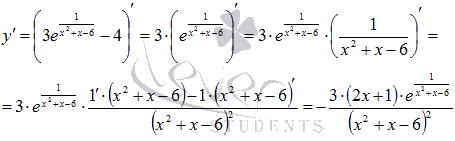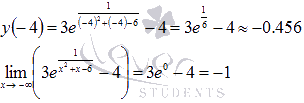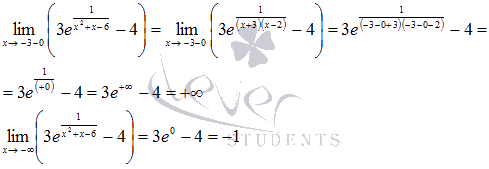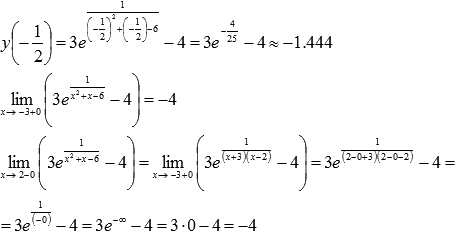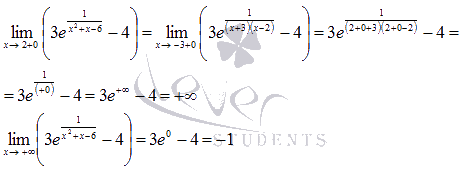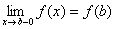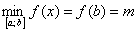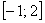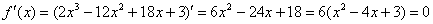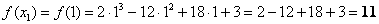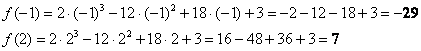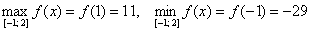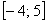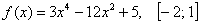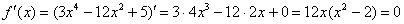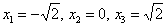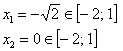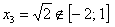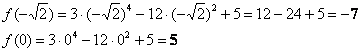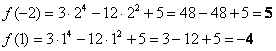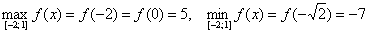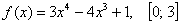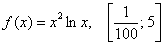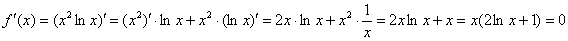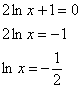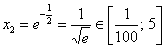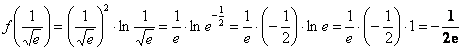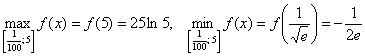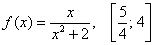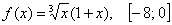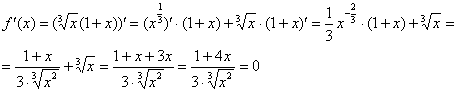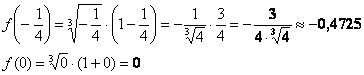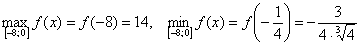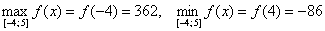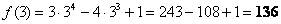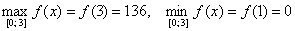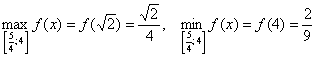Что значит найти наименьшее значение функции

Наибольшее и наименьшее значение функции.

С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования. Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.

Навигация по странице.

Кратко остановимся на основных определениях.

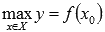
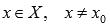
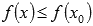
Наибольшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

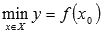
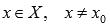
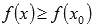
Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .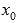

Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.

Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.

Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.

Сразу ответим на один из самых распространенных вопросов по этой теме:»Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.

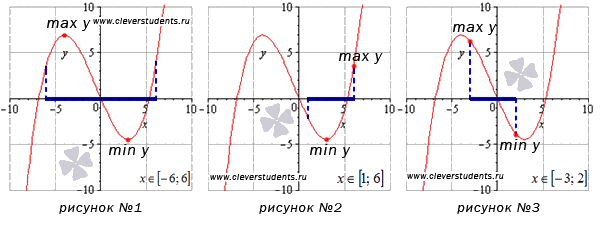
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.

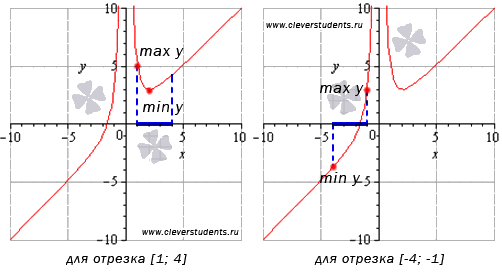
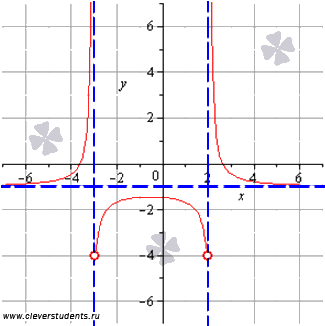
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.

На открытом интервале

На интервале [1;6) наименьшее значение функции достигается в стационарной точке, а про наибольшее значение мы ничего сказать не можем. Если бы точка x=6 была частью интервала, тогда при этом значении функция принимала бы наибольшее значение. Этот пример изображен на рисунке №5.

Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.

Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.

Областью определения функции является все множество действительных чисел, за исключением нуля, то есть 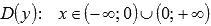. Оба отрезка попадают в область определения.

Находим производную функции по правилу дифференцирования дроби:

Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1] (так как он не содержит ни одной стационарной точки):

Следовательно, .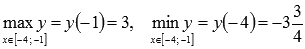

Прежде чем ознакомиться с алгоритмом нахождения наибольшего и наименьшего значения функции на открытом или бесконечном интервале рекомендуем повторить определения одностороннего предела и предела на бесконечности, а также способы нахождения пределов.

Проверяем, является ли интервал X подмножеством области определения функции.

Находим все точки, в которых не существует первая производная и которые содержатся в интервале X (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.

Если стационарных точек нет или ни одна из них не попадает в интервал, то переходим к следующему пункту.

Вычисляем значения функции в стационарных точках и точках, в которых не существует первая производная функции (если такие точки есть).

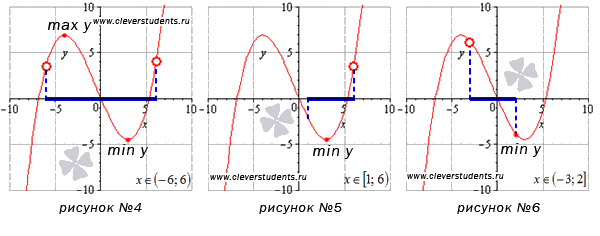
Делаем выводы, отталкиваясь от полученных значений функции и пределов. Здесь может быть масса вариантов. К примеру, если односторонний предел равен минус бесконечности (плюс бесконечности), то о наименьшем (наибольшем) значении функции ничего сказать нельзя для данного интервала. Ниже разобраны несколько типичных примеров. Надеемся подробные описания их решения помогут Вам усвоить тему. Рекомендуем вернуться к рисункам с №4 до №8 из первого раздела этой статьи.

Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:

Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.

Продифференцируем функцию:

Очевидно, производная существует на всей области определения функции.

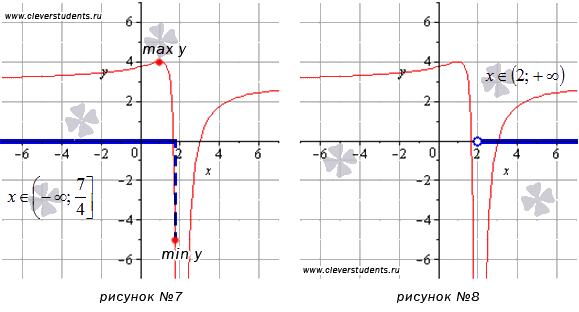
Для первого промежутка 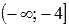вычисляем значение функции при x=-4 и предел на минус бесконечности:

Второй интервал 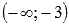интересен тем, что не содержит ни одной стационарной точки и ни одна из его границ не является строгой. В этом случае мы не сможем найти ни наибольшего, ни наименьшего значения функции. Вычислив предел на минус бесконечности и при стремлении аргумента к минус трем слева, мы лишь сможем определить интервал значений функции:

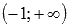
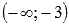
Следовательно, значения функции находятся в интервале при x из промежутка .

Для интервала (-3;2) воспользуемся результатами из предыдущего пункта и еще вычислим односторонний предел при стремлении к двойке слева:

На промежутке 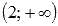функция не достигает ни наибольшего, ни наименьшего значения.

То есть, на этом интервале функция принимает значения из промежутка .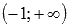

А теперь можно сопоставить полученные в каждом пункте результаты с графиком функции. Синими пунктирными линиями обозначены асимптоты.

На этом можно закончить с нахождением наибольшего и наименьшего значения функции. Алгоритмы, разобранные в этой статье, позволяют получить результаты при минимуме действий. Однако бывает полезно сначала определить промежутки возрастания и убывания функции и только после этого делать выводы о наибольшем и наименьшем значении функции на каком-либо интервале. Это дает более ясную картину и строгое обоснование результатов.

Источник

Наибольшее и наименьшее значение функции

На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.

Основные определения

Начнем, как всегда, с формулировки основных определений.

Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.

Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.

Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.

Более понятными эти моменты станут после изображения на графиках:

Наибольшее и наименьшее значение функции на отрезке

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

Наибольшее и наименьшее значение функции на открытом интервале

Наибольшее и наименьшее значение функции на бесконечности

Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке

В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.

Посмотрим, как правильно применить этот алгоритм при решении задач.

Решение:

Теперь вычисляем производную функции согласно правилу дифференцирования дроби:

y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4

Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

Решение

Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :

Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:

Следовательно, производные функции существуют на всей области ее определения.

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

Источник

Наибольшее и наименьшее значения функции на отрезке

Миниатюрная и довольно простая задача из разряда тех, которые служат спасательным кругом плавающему студенту. На природе сонное царство середины июля, поэтому самое время устроиться с ноутбуком на пляже. Ранним утром заиграл солнечный зайчик теории, чтобы в скором времени сфокусироваться на практике, которая, несмотря на заявленную лёгкость, содержит осколки стекла в песке. В этой связи рекомендую добросовестно рассмотреть немногочисленные примеры этой странички. Для решения практических заданий необходимо уметь находить производные и понимать материал статьи Интервалы монотонности и экстремумы функции.

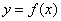
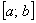
Сначала коротко о главном. На уроке о непрерывности функции я приводил определение непрерывности в точке и непрерывности на интервале. Образцово-показательное поведение функции на отрезке формулируется похожим образом. Функция непрерывна на отрезке если:

1) она непрерывна на интервале ;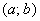
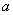
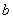
2) непрерывна в точке справа и в точке слева.

Во втором пункте речь зашла о так называемой односторонней непрерывности функции в точке. Существует несколько подходов к её определению, но я буду придерживаться начатой ранее линии:

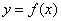
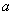
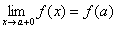
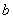
Функция непрерывна в точке справа, если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке: . Она же непрерывна в точке слева, если определена в данной точке и её левосторонний предел равен значению в этой точке:

Представьте, что зелёные точки – это гвозди, на которых закреплена волшебная резинка:

Мысленно возьмите красную линию в руки. Очевидно, что как бы далеко мы не растягивали график вверх и вниз (вдоль оси ), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне. Таким образом, непрерывная на отрезке функция ограничена на нём. В курсе матанализа этот вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса. …Многих раздражает, что в математике нудно обосновываются элементарные утверждения, однако в этом есть важный смысл. Предположим, некий житель махрового средневековья вытягивал график в небо за пределы видимости вот это вставляло. До изобретения телескопа ограниченность функции в космосе была вовсе не очевидна! Действительно, откуда вы знаете, что нас ждёт за горизонтом? Ведь когда-то и Земля считалась плоской, поэтому сегодня даже обыденная телепортация требует доказательства =)

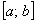
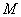
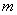
Согласно второй теореме Вейерштрасса, непрерывная на отрезке функция достигает своей точной верхней грани и своей точной нижней грани .

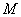
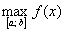
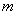
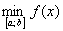
Число также называют максимальным значением функции на отрезке и обозначают через , а число – минимальным значением функции на отрезке с пометкой .

В нашем случае: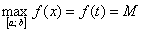

Примечание: в теории распространены записи .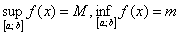

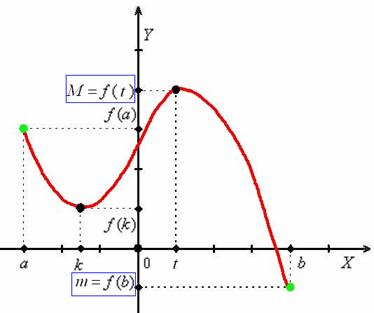
Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка.

Важно! Как уже заострялось внимание в статье об экстремумах функции, наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ, что максимум функции и минимум функции. Так, в рассматриваемом примере число 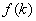является минимумом функции, но не минимальным значением.

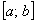
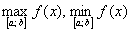
Кстати, а что происходит вне отрезка ? Да хоть потоп, в контексте рассматриваемой задачи это нас совершенно не интересует. Задание предполагает лишь нахождение двух чисел и всё!

Более того, решение чисто аналитическое, следовательно, чертежа делать не надо!

Алгоритм лежит на поверхности и напрашивается из приведённого рисунка:

1) Находим значения функции в критических точках, которые принадлежат данному отрезку.

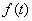
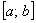
Ловите ещё одну плюшку: здесь отпадает необходимость проверять достаточное условие экстремума, поскольку, как только что было показано, наличие минимума или максимума ещё не гарантирует, что там минимальное или максимальное значение. Демонстрационная функция достигает максимума и волей судьбы это же число является наибольшим значением функции на отрезке . Но, понятно, такое совпадение имеет место далеко не всегда.

Итак, на первом шаге быстрее и проще вычислить значения функции в критических точках, принадлежащих отрезку, не заморачиваясь есть в них экстремумы или нет.

2) Вычисляем значения функции на концах отрезка.

3) Среди найденных в 1-м и 2-м пунктах значений функции выбираем самое маленькое и самое большое число, записываем ответ.

Садимся на берег синего моря и бьём пятками по мелководью:

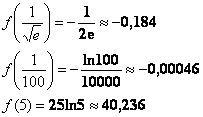
Найти наибольшее и наименьшее значения функции 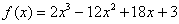на отрезке

Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:

Полученное квадратное уравнение имеет два действительных корня:
– критические точки.

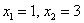
Ещё раз подчёркиваю, что нас не интересует, есть в них максимумы/минимумы или нет.

Первая критическая точка принадлежит данному отрезку: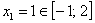
А вот вторая – нет: 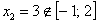, поэтому про неё сразу забываем.

Вычислим значение функции в нужной точке:

Итоговый результат я выделил жирным цветом, при оформлении задания в тетради его удобно обвести в кружок простым карандашом или пометить как-то по-другому.

2) Вычислим значения функции на концах отрезка:

Результаты опять каким-либо образом выделяем.

3) Дело сделано, среди «жирных» чисел выбираем наибольшее и наименьшее.

Ответ:

Критическое значение 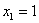на поверку оказалось точкой максимума, но об этом нас никто не спрашивал. Впрочем, для саморазвития можете устно подмечать такие факты.

Найти наибольшее и наименьшее значения функции 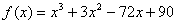на отрезке

Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.

В рассматриваемой задаче очень важно не допускать вычислительных ошибок, так как рецензент немедленно посмотрит, сами догадываетесь куда.

Другой существенный момент касается пункта № 1.

Во-первых, критических точек может не оказаться вообще. Это очень хорошо – меньше вычислений. Просто записываем вывод: «критические точки отсутствуют» и переходим ко второму пункту алгоритма.

Во-вторых, все критические точки (одна, две или бОльшее количество) могут не принадлежать отрезку. Замечательно. Пишем следующее: «критические точки (а) не принадлежат (ит) рассматриваемому отрезку». Находить какие-то значения функции здесь, разумеется, тоже не надо.

В моей коллекции есть и те и те примеры, но они унылы как бескрайние просторы Сахары. По сути, всё задание сводится к нахождению двух значений функции на концах интервала. Гораздо интереснее снять кепки, солнечные очки и отправиться играть в пляжный футбол:

Найти наибольшее и наименьшее значения функции на заданном отрезке

Решение: всё опять начинается дежурной фразой:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:

Да, критических точек тут и правда целая команда:

Первые две точки принадлежат нашему отрезку:

Но третья оказывается вне игры:

(надеюсь, все сумели сосчитать )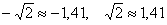

Вычислим значения функции в подходящих точках:

Чтобы не заблудиться в трёх соснах, не забываем выделять результаты,

2) Вычислим значения функции на концах отрезка:

Среди «жирных» чисел выбираем наибольшее и наименьшее значения. Максимальное значение («пятёрка») достигается сразу в двух точках, и это необходимо указать в завершающей записи:

Ответ:

Время от времени критические точки могут совпадать с одним или даже с обоими концами отрезка, и в этом случае укорачивается второй этап решения. Следующий пример для самостоятельного изучения посвящен как раз такой ситуации:

Найти наибольшее и наименьшее значения функции на заданном отрезке

Примерный образец решения в конце урока.

Иногда техническая трудность рассматриваемого задания состоит в замысловатой производной и громоздких вычислениях:

Найти максимальное и минимальное значения функции на отрезке

Решение: отрезок, надо сказать, творческий, но пример взят из конкретной контрольной работы и ни в коем случае не придуман.

1) Вычислим значения функции в критических точках, которые принадлежат данному отрезку:

Очевидный корень оказывается не в теме: .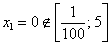

Решаем уравнение:

Второй корень принадлежит нашему отрезку:

Если вам не понятно, почему именно такой корень, обязательно обратитесь к школьному учебнику Алгебра и начала анализа 10-11 класс и повторите, что такое логарифм, ибо плох тот студент, который не мечтает овладеть логарифмами.

Дальнейшие вычисления задачи я распишу максимально подробно, но без комментариев. Некоторую информацию о логарифмической функции и свойствах логарифма можно почерпнуть в статье Графики и свойства элементарных функций и методичке по школьным формулам.

Вычислим значение функции во второй критической точке:

2) Вычислим значения функции на концах отрезка:

3) «Жирные» результаты получены с экспонентами и логарифмами, что существенно затрудняет их сравнение. По сей причине вооружимся калькулятором либо Экселем и вычислим приближённые значения, не забывая, что :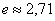

Вот теперь всё понятно.

Ответ:

Дробно-рациональный экземпляр для самостоятельного решения:

Найти максимальное и минимальное значения функции на отрезке

Вычисления в данном случае не менее кропотливы и точно так же потребуют вмешательства калькулятора (если вы, конечно, не вундеркинд). Полное решение и ответ в конце урока.

Стрелки часов приближаются к 9 утра, и побережье потихоньку заполняется всё бОльшим и бОльшим количеством стройных ног. Если честно, не терпится захлопнуть ноут и похулиганить, но всё-таки мужественно разберу нетривиальную вещь:

Найти максимальное и минимальное значения функции на отрезке

Решение:
1) Найдём критические точки. Предварительно можно раскрыть скобки, но не особо сложнее использовать и правило дифференцирования произведения:

– критические точки.

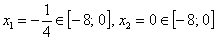
Обратите внимание, что точка 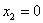обращает знаменатель производной в ноль, но её следует отнести к критическим значениям, поскольку САМА ФУНКЦИЯ определена в данной точке. На этом случае я подробно останавливался в теоретической части и последнем примере урока Интервалы монотонности. Экстремумы функции.

Кроме того, данная точка совпала с правым концом отрезка, а значит, в следующем пункте будет меньше расчётов. В следующем, но не сейчас:

2) Вычислим значения функции на концах отрезка: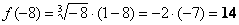

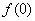
уже известно.

Ответ:

Раз, два, три, четыре, пять – мне пора верстать.

Скорее всего, вы прочитали данную статью в ненастную погоду, поэтому желаю всем скорейшего летнего загара без зачётки в кармане! …ну или с дипломом на груди… …ой, что-то я не то сказал =)

Пример 2: Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:

– критические точки.

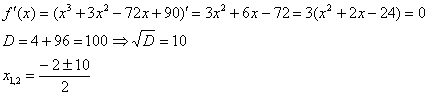
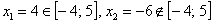
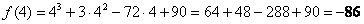
2)Вычислим значения функции на концах отрезка: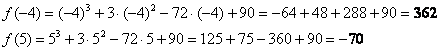

Ответ:

Пример 4: Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:

– критические точки.

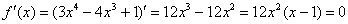
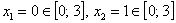
2) Вычислим значения функции на концах отрезка:
уже рассчитано в предыдущем пункте.

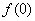
Ответ:

Пример 6: Решение:
1) Вычислим значения функции в критических точках, которые принадлежат данному отрезку: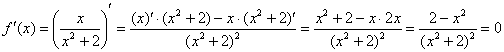
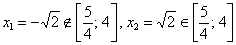
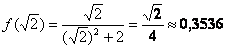
– критические точки.

2) Вычислим значения функции на концах отрезка: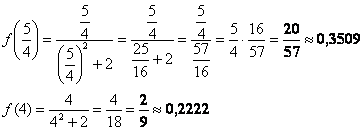

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник