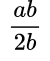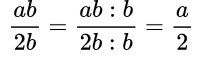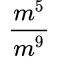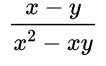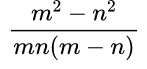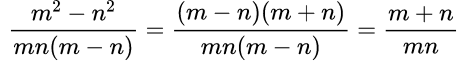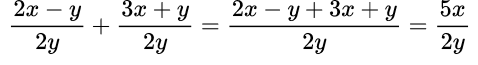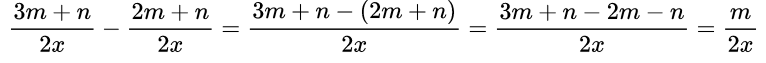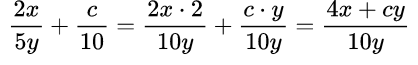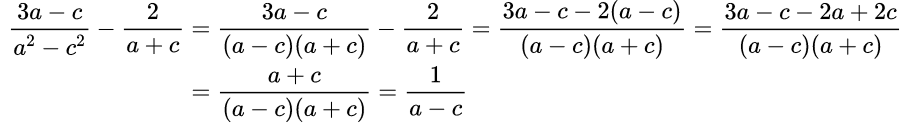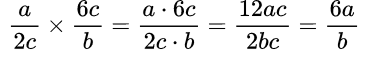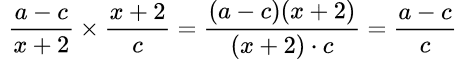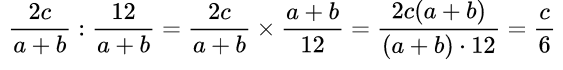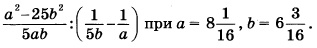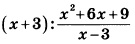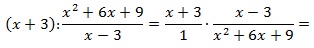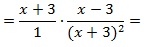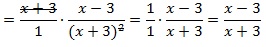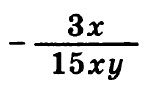Что значит найдите область определения алгебраических дробей

Область допустимых значений (ОДЗ): теория, примеры, решения

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Решение

Решение

Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

Рассмотрим на примере.

Рассмотрим пример с наличием подкоренного выражения.

Нужно избегать преобразований, которые сужают ОДЗ.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

При наличии логарифмов дело обстоит немного иначе.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.

Источник

Алгебраические дроби

теория по математике 📈 алгебраические выражения

Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения.

Примеры алгебраических дробей:

Для алгебраических дробей применяются правила, аналогичные обыкновенным дробям.

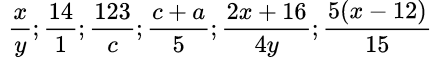
Сокращение алгебраической дроби

Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на одно и то же выражение, на их общий множитель (одночлен, его степень или многочлен) – применяется основное свойство дроби. Причем и числитель, и знаменатель должны содержать множители.

Пример №1. Сократим дробь:

В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:

Промежуточные действия можно не записывать, а выполнять устно.

Пример №2. Сократим дробь:

Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на m 5 :

Пример №3. Сократим дробь:

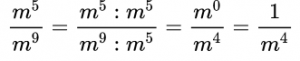
В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).

Пример №4. Сократим дробь:

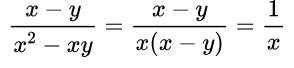
Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m 2 – n 2 =(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).

Сложение и вычитание алгебраических дробей с одинаковым знаменателем

При сложении и вычитании алгебраических дробей с одинаковыми знаменателями знаменатель остается прежним, а числители складывают или вычитают (из числителя первой вычитают числитель второй дроби).

Пример №5. Выполним сложение дробей:

Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.

Пример №6. Выполним вычитание дробей:

В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.

Сложение и вычитание алгебраических дробей с разными знаменателями

Чтобы сложить или вычесть дроби с разными знаменателями, необходимо:

Пример №7. Выполнить сложение дробей:

Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.

Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.

Пример №8. Выполнить вычитание дробей:

Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а 2 – с 2 =(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).

Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).

Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).

Умножение алгебраических дробей

Чтобы перемножить алгебраические дроби, надо числитель перемножить с числителем, а знаменатель со знаменателем. При необходимости выполнить сокращение алгебраической дроби, используя правило.

Пример №9. Выполнить умножение дробей:

Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.

Пример №10. Выполнить умножение дробей:

Здесь в числителях и знаменателях — многочлены. Поэтому при записи умножения обязательно заключаем их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.

Деление алгебраических дробей

Чтобы разделить одну алгебраическую дробь на другую, надо первую дробь умножить на дробь, обратную второй (то есть умножить на дробь, у которой числитель равен знаменателю второй дроби, а знаменатель числителю второй дроби). Далее – выполнить умножение дробей по уже известному алгоритму.

Пример №11. Выполнить деление дробей:

Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.

Найдите значение выражения:

Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:

сокращаем выражение на (a–5b): Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): Подставим полученные значения в выражение и найдем конечный результат: Ответ: 39

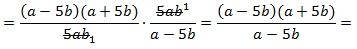
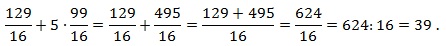
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения при x = 12:

Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:

далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):

теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:

Подставляем числовое значение для х в полученное выражение и находим результат:

Ответ: 0,6

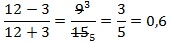
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения

В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:

Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:

Вычислим её значение, подставив числа из условия:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:

5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x

Тогда дробь примет вид:

Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y

Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

Алгебраические дроби

Тема 7 «Алгебраические дроби»

Цель главы – выработать у учащихся устойчивые навыки действий с алгебраическими дробями.

Вы познакомитесь с алгебраическими дробями, у которых числитель и знаменатель — целые буквенные выражения, научитесь складывать, вычитать, умножать и делить алгебраические дроби.

1. Определение алгебраической дроби.

В седьмом и восьмом классах рассматривались целые буквенные выражения. Такими выражениями являются многочлены от одной или нескольких переменных. Например, , , , , .

Иногда целые буквенные выражения называют целыми алгебраическими выражениями.

Напомним, что при подстановке в целое алгебраическое выражение вместо букв некоторых чисел получается числовое выражение. Значение этого числового выражения называют значением целого алгебраического выражения при заданном наборе переменных. Например, целое выражение при и имеет значение, равное .

Целые буквенные выражения удобны для записи некоторых формул, функций и для других целей.

2. Значение алгебраической дроби.

Для целых многочленов были определены сложение, вычитание и умножение. Изучая многочлены от одной переменной, мы установили, что разделить без остатка один многочлен на другой и получить частное в виде многочлена удается не всегда. Чтобы для буквенных выражений можно было рассмотреть деление, определяют алгебраические дроби.

Отношение двух целых алгебраических выражений называется алгебраической дробью.

Вот несколько примеров алгебраических дробей:

У алгебраической дроби, как и у числовых дробей, имеются числитель и знаменатель.

Числителем алгебраической дроби называют выражение, стоящее над дробной чертой.

Знаменателем алгебраической дроби называют выражение, стоящее под дробной чертой. Для краткости алгебраическую дробь называют дробью, когда из текста ясно, о каких дробях идет речь.

3. Область определения дроби.

Подставляя в алгебраическую дробь вместо букв конкретные числа, мы будем получать числовые выражения. При некоторых значениях переменных значение знаменателя может оказаться равным нулю. Но так как на нуль делить нельзя, то для таких значений переменных вычислить значение алгебраической дроби не удается. Будем говорить, что алгебраическая дробь не определена при наборах значений переменных, для которых значение знаменателя дроби равно нулю.

Пример 1. Дробь имеет знаменатель , который обращается в нуль при . Поэтому данная дробь не определена при .

Пример 2. Дробь имеет знаменатель , который тождественно равен нулю. Поэтому данная дробь не определена ни при каком значении .

Пример 3. Дробь имеет знаменатель , который обращается в нуль при . Поэтому данная дробь не определена, если брать равные значения переменных и .

4. Так как алгебраическая дробь при некоторых значениях переменных может быть не определена, то это надо учитывать при действиях с дробями, рассматривая только такие значения переменных, для которых дроби определены и выполнимы все арифметические операции.

Множество значений переменных, при которых данная алгебраическая дробь определена, называют областью определения данной дроби.

Область определения для алгебраической дроби с несколькими переменными задавать сложно. Поэтому мы будем рассматривать области определения только для алгебраических дробей с одной переменной, например, с переменной . В этом случае дробь имеет вид , где и — многочлены.

Задавая алгебраическую дробь, иногда указывают и ее область определения.

Пример 4. Дробь рассматривается при всех действительных , отличных от 2. В этом примере область определения дроби состоит из всех действительных чисел, не равных 2, и может быть записана в виде объединения двух промежутков:

Пример 5. Если нас интересуют значения дроби для положительных , то область определения этой дроби можно считать равной интервалу .

Пример 6. Дробь рассматривается при всех натуральных . В данном примере область определения дроби — это множество всех натуральных чисел.

Часто область определения алгебраической дроби не указывается. В этом случае будем предполагать, что область определения дроби — множество всех действительных чисел, при которых значения данной дроби определены.

Пример 7. Записывая дробь , мы будем предполагать, что она определена при действительных .

Пример 8. Записывая дробь , мы будем предполагать, что она определена при действительных .

5.** Зависимость области определения дроби от числового множества.

Область определения алгебраической дроби зависит от числового множества, в котором рассматриваются значения переменной.

Пример 9. Дробь всюду определена, если рассматриваются только натуральные значения переменной . И эта же дробь не всюду определена, если рассматривать целые значения , так как при дробь не определена.

Пример 10. Дробь всюду определена, если рассматривать только целые значения переменной . И эта же дробь не всюду определена, если рассматривать рациональные значения , так как при дробь не определена.

Пример 11. Дробь всюду определена, если рассматривать только рациональные значения переменной . И эта же дробь не всюду определена, если рассматривать действительные значения , так как при и при дробь не определена.

Еще раз обратим внимание, что когда область определения дроби не указана, то мы ее рассматриваем на множестве всех действительных чисел, при которых значения данной дроби определены.

6. Основное свойство алгебраической дроби

Рассмотрим числовую дробь . Значение этой дроби не изменится, если мы умножим числитель и знаменатель на одно и то же не равное нулю число. Например,

Аналогичное свойство выполнено и для алгебраических дробей. Оно называется основным свойством алгебраической дроби.

Значение алгебраической дроби не изменится, если числитель и знаменатель дроби умножить на один и тот же множитель, значение которого отлично от нуля.

Иногда основное свойство алгебраической дроби формулируют по-другому:

алгебраическая дробь не изменится, если числитель и знаменатель дроби умножить на один и тот же множитель, не обращающийся в нуль в области определения данной алгебраической дроби.

При этом подразумевается, что значения дроби и дроби рассматриваются на общей части их областей определения.

7. Сокращение алгебраической дроби.

Рассмотрим дроби и . По основному свойству дробей эти дроби равны на общей части их областей определения, то есть

при .

Перепишем равенство в виде

Правая часть этого равенства получается из левой части сокращением числителя и знаменателя на один и тот же множитель . Будем говорить, что дробь получается из дроби сокращением числителя и знаменателя на общий множитель.

При сокращении числителя и знаменателя на общий множитель часто получается дробь с меньшими степенями числителя и знаменателя.

Пример 14. .

В этом примере мы сократили дробь на числовой множиПоэтому области определения дробей и одинаковы, и равенство выполняется при любом .

Пример 15. .

В этом примере мы сократили дробь на множитель . Однако, левая дробь не определена ни при каком значении . Поэтому записанное равенство не выполняется ни при одном значении .

Пример 16. .

Это равенство выполняется только при таких значениях и , при которых определены как первая, так и последняя дроби, то есть и .

8.** Тождественное равенство дробей на некотором множестве. Свойства рефлексивности, симметричности, транзитивности.

Использование знака равенства при действиях с алгебраическими дробями имеет более сложный смысл, чем при действиях с многочленами. Чтобы в этом разобраться, определим тождественное равенство двух алгебраических дробей от переменной на некотором множестве чисел.

Алгебраические дроби и тождественно равны на множестве , если при каждом значения и определены и равны.

Тождественное равенство дробей и записывают с помощью знака , вместо которого иногда используют обычный знак равенства, когда из текста ясно, что речь идет о тождественном равенстве алгебраических дробей на некотором множестве.

Тождественное равенство алгебраических дробей от переменной обладает следующими основными свойствам.

Свойство 1. Пусть дробь определена на множестве . Тогда на множестве .

Свойство 2. Пусть на множестве . Тогда на множестве .

Свойство 3. Пусть на множестве и и на множестве . Тогда на пересечении множеств и . При , имеем равенство .

Пример 17. При , имеем равенство . Поэтому на основании свойства 3 при , , имеем равенство

1. Что такое целое алгебраическое выражение?

2. Что такое алгебраическая дробь?

3. Дайте определение числителя и знаменателя алгебраической дроби.

4. При каких значениях переменных алгебраическая дробь не определена?

5. Каким условиям должна удовлетворять область определения алгебраической дроби?

6. Как находить область определения алгебраической дроби в том случае, когда эта область не указана?

7. Сформулируйте основное свойство алгебраической дроби.

8. Что называют сокращением алгебраической дроби?

9. Что нужно сделать, чтобы сократить алгебраическую дробь, если это возможно?

Задачи и упражнения

1. При каких значениях переменной определена алгебраическая дробь:

а) б) ; в) ; ;

г) д) ; е) ; ж) ; ?

2. Сократите алгебраическую дробь:

а) б) ; в) ; г) ; ;

д) е) ; ж) ; .

3. Укажите, при каких значениях переменных исходная дробь равна той дроби, которая получается после сокращения.

Сократите алгебраическую дробь:

а) б) ; в) ; ;

г) д) ; е) ; ж) ; .

4. Сократите алгебраическую дробь:

а) б) ; в) ; ;

г) д) ; е) ; .

Ответы и указания к решению наиболее трудных задач.

Задача 4. Указание. а) , .

б) , .

в) Если , то рассматриваемая дробь не имеет смысла, поэтому . Сократив числитель и знаменатель на и приведя подобные члены получим выражение . Если ввести новую переменную , то в результате получим алгебраическую дробь вида . Корнями уравнения являются числа и , поэтому . Так что сократить можно только на числовой множитель.

г) при всех и таких, что и .

д)
при всех и таких, что и .

е) при всех таких и , что и .

Источник