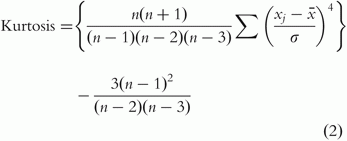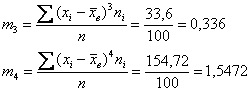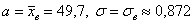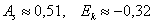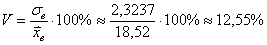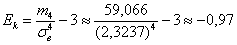Что значит эксцесс в статистике
коэффициент эксцесса
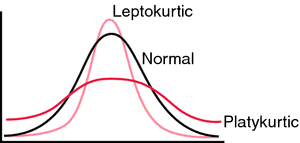
коэффициент эксцесса (Kurtosis) — в статистике — мера остроты пика в распределении случайной величины.
эксцесс характеризует распределения, в которых значения величин либо сосредоточены близко к средней величине, либо наоборот распределены далеко от нее.
положительный эксцесс (leptokurtic) — острая вершина, когда пик выше чем пик нормального распределения.
отрицательный эксцесс (platykurtic) — тупая вершина, когда пик ниде пика нормального распределения).
Как правило, доходы от рынка акций распределены с положительным эксцессом.
Если мы используем распределение с положительным эксцессом, то мы недооцениваем риск очень плохого или очень хорошего сценария.
19 октября 1987 изменение S&P500 за день отстояло на 20 стандартных отклонений от среднего дневного изменения. Вероятность такого события равна нулю, если применять нормальное распределение.
Если дневные доходы распределены нормально, то вероятность события отстоящего на 4 сигмы (станд. откл.) равна 1 раз в 50 лет. Величина которая отстоит больше чем на 5 сигм — 1 раз в 7000 лет.
Исходя из этого, можно заключить, что нормальное распределение лучше описывает годовые изменения индекса S&P500, чем месячные или ежедневные.
7. Асимметрия и эксцесс эмпирического распределения
В предыдущих статьях мы познакомились с показателями центральной тенденции и вариации, и сейчас рассмотрим ещё пару характеристик статистической совокупности. Для тех, кто зашёл с поисковика и хочет изучить тему с азов, сразу ссылка на организационный урок: Математическая статистика для «чайников», там же, в конце, список всех статей курса. И до статьи 7-й – как рукой подать, после чего будет небольшой и очень приятый экзамен.
Итак, что такое асимметрия и эксцесс? Говоря простым языком, это показатели, характеризующие геометрическую форму распределения. Асимметрия характеризует меру скошенности графика влево / вправо, а эксцесс – меру его высоты.
Данные показатели рассчитываются как для эмпирических, так и для теоретических распределений, которые мы изучили в курсе теории вероятностей, и за «эталон» симметрии принято нормальное распределение: 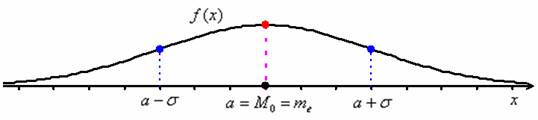
Очевидно, что любое нормальное распределение строго симметрично относительно своего центра, следовательно, его асимметрия равна нулю. Данный график кажется пологим, но стандартное отклонение 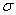
Почему именно нормальное распределение? Потому что философское – обязательно прочитайте эту интереснейшую статью по ссылке, если ещё не успели этого сделать!
В теории вероятностей существуют строгие формулы для вычисления коэффициентов асимметрии 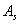
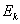
Начнём с асимметрии. Асимметрия характеризует меру скошенности полигона или гистограммы влево / вправо относительно самого высокого участка, и во многих случаях для «прикидки» асимметрии достаточно взглянуть на соответствующие чертежи. Так, например, посмотрим на полигон частот из Примера 8: 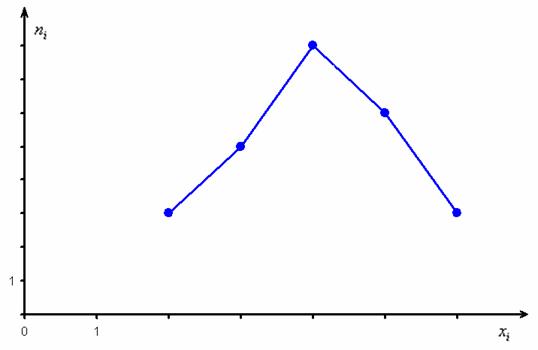
И, в принципе, тут всё видно – пациент скорее симметричен, чем асимметричен 🙂
Простейшим критерием симметрии является равенство средней, моды и медианы: но в жизни такого идеального совпадения, конечно, не бывает (даже тело человека немного асимметрично), и поэтому у «почти симметричных» распределений эти показатели должны располагаться очень близко друг к другу. И в самом деле, как мы вычислили в Примере 8: 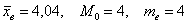
Обратите внимание, что рассматриваемые распределения имеют единственную модальную вершину, и далее речь пойдёт только о таких распределениях.
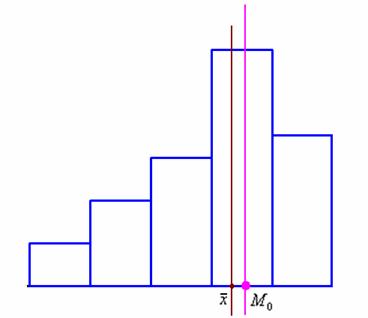
Правосторонняя асимметрия характеризуется удлинённым правым «хвостом», смотрим на гистограмму Примера 10:
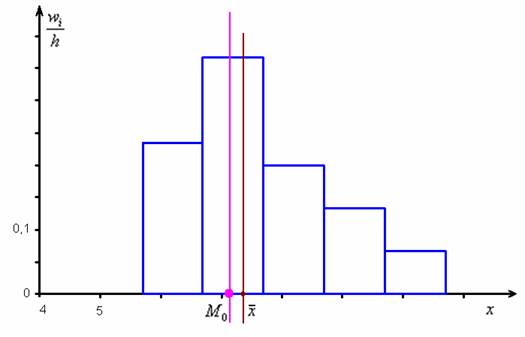
Простейшим признаком правосторонней асимметрии является тот факт, что 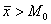
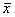
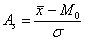
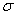
Левостороння асимметрия, наоборот, характеризуются удлинённым левый «хвостом» и неравенством 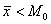
Из формулы 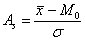
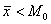
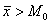
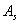
Недостаток формулы Пирсона состоит в том, что она описывает лишь центральную часть распределения и практически не учитывает «периферию». И, чтобы вас томить, сразу продвинутая формула, которая охватывает все варианты, для определённости запишу её для выборочной совокупности объёма 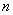
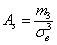
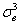
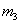
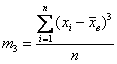
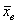
а для сформированного вариационного ряда – так: 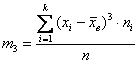
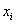
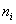
Смысл знаков тот же самый: если 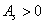
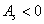
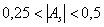
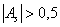
И чем МЕНЬШЕ по модулю 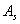
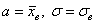
Справочно формулы теории вероятностей: асимметрия случайной величины рассчитывается по «родственной» формуле 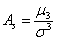
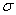
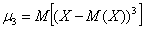
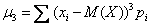
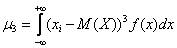
Теперь об эксцессе замолвим слово. Он характеризует высоту и очень коварный. В том смысле, что глаза будут часто обманывать. Так, например, вернёмся к Примеру 7 статьи Интервальный вариационный ряд, единственное, я рассмотрю равные интервалы, как это на самом деле было в оригинальной задаче:
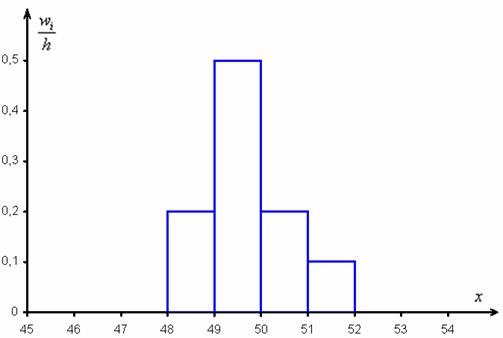
Ну видно же – гистограмма серьёзно вытянута вверх. Но это только кажется. Дело в том, что стандартное отклонение 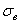
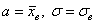
Поэтому аналитика и ещё раз аналитика. Коэффициент эксцесса эмпирического распределения рассчитывается по формуле:
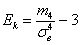
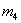
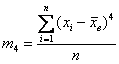
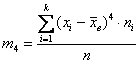
Для случайных величин из тервера формула схожа: 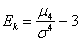
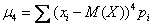
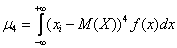
Если 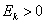
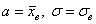
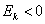
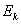
В примере выше, как ни странно, 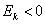
Итак, сто пачек чая из Примера 7 ( 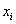
и нам требуется вычислить коэффициенты асимметрии и эксцесса
Решение: поскольку в формулах асимметрии и эксцесса фигурирует стандартное отклонение, то сначала нужно рассчитать выборочную среднюю и дисперсию.
Вычислим произведения 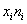
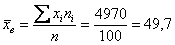
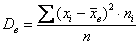
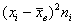
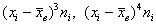
Ловкость рук и никаких трудностей, вы удивитесь, как всё быстро:
Собственно, финальные расчёты: 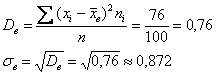
здесь правильнее, конечно, отклонение поправить, но обычно этим пренебрегают.
Центральные моменты 3-го и 4-го порядков:
И, наконец, коэффициенты. Вычислим коэффициент асимметрии: 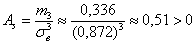
Вычислим коэффициент эксцесса:
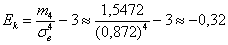
Ответ:
Вот такой вот у нас получился эксекас 🙂
Помимо геометрических форм, эти коэффициенты позволяют «прикинуть», насколько близка к нормальному (или другому) распределению не только выборочная, но и вся генеральная совокупность. Это одна из важнейших задач статистики, которую мы разберём в разделе Статистические гипотезы.
Ну а сейчас я предлагаю вам небольшое экзаменационное задание по первым семи урокам. Оно типично для студенческой практики – дана статистическая совокупность, и требуется выполнить много-много чего. Внимательно проверьте, всё ли вы усвоили, всё ли умеете:
В результате эксперимента получены данные, записанные в виде статистического ряда: 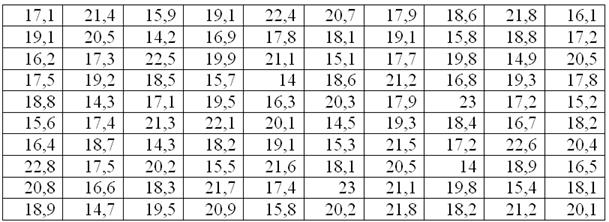
…это ещё ерунда 🙂
И сразу обратите внимание, что в условии речь идёт о результатах эксперимента, а значит, перед нами выборочная совокупность, т.к. теоретически опыты можно повторять бесконечное количество раз.
1) Составить интервальный вариационный ряд, состоящий из 9 равных интервалов. Видео в помощь.
3) Найти моду и медиану.
5) Вычислить коэффициенты асимметрии и эксцесса, сделать выводы.
Не тушуйтесь – я с вами! Краткое решение для сверки внизу страницы.
И на этом, как вы правильно догадались, дело не заканчивается, поэтому сохраните файл с решением! Типовая задача содержит больше пунктов, и после изучения гипотезы о законе распределения генеральной совокупности, выполняем следующие задания:
6) По найденным характеристикам сделать вывод о форме эмпирического ряда распределения.
7) Построить нормальную кривую по опытным данным на графике гистограммы.
8) Произвести оценку степени близости теоретического распределения эмпирическому ряду с помощью критерия согласия Пирсона на уровне значимости 0,05.
Пример 20. Решение:
1) По статистическим данным находим: 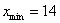
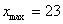
Вычислим размах вариации: 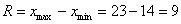
По условию, выборку следует разделить на 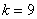
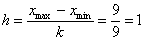
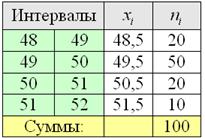
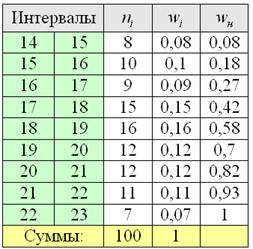
Разметим интервалы и подсчитаем частоты 
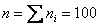
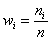
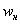
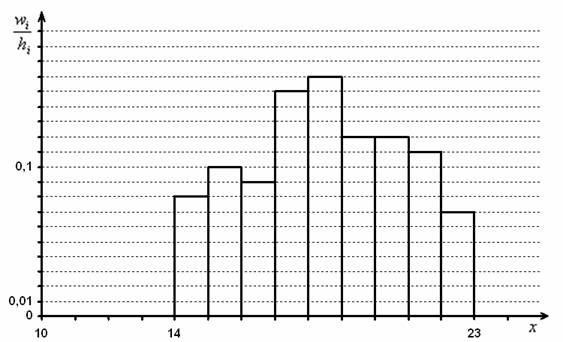
2) Построим гистограмму относительных частот. Поскольку длина частичного интервала 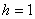
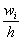
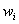
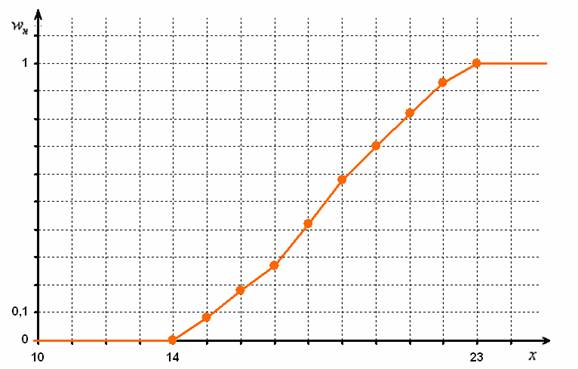
Построим эмпирическую функцию распределения:
3) Моду вычислим по формуле 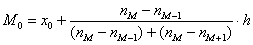
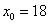
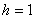
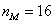
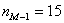
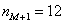
Таким образом:
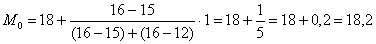
Медиану вычислим по формуле 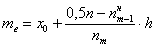
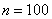
половину вариант содержит интервал 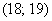
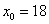
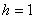
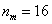
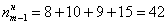
Таким образом:
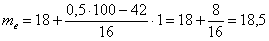
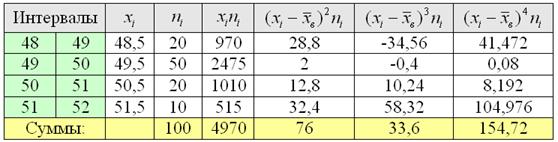
4) Найдём середины 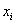
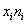
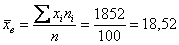
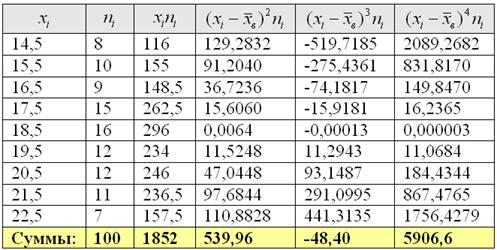
Выборочная дисперсия: 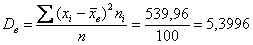
выборочное среднее квадратическое отклонение:
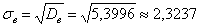
коэффициент вариации:
5) Вычислим центральные эмпирические моменты 3-го и 4-го порядков: 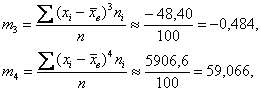
коэффициент асимметрии: 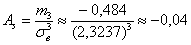
и коэффициент эксцесса:
Таким образом, выборочная совокупность практически симметрична, но несколько ниже, чем нормальное распределение с параметрами 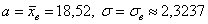
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5