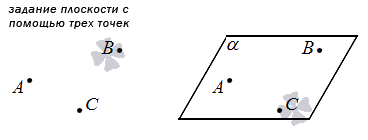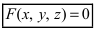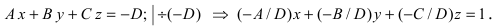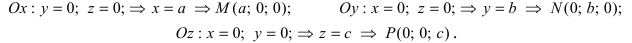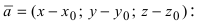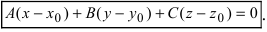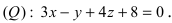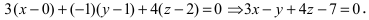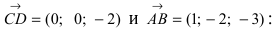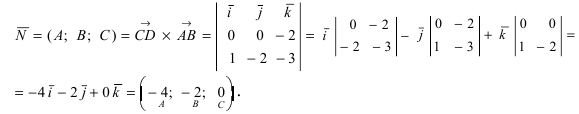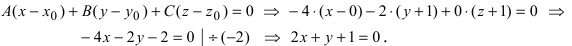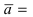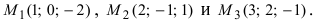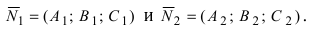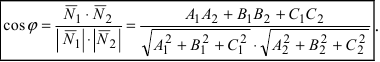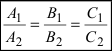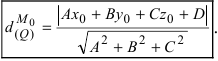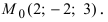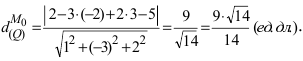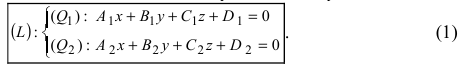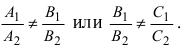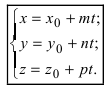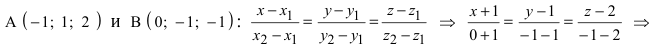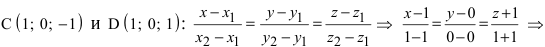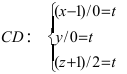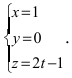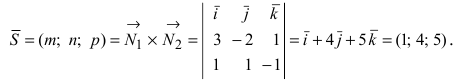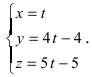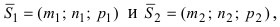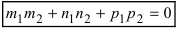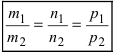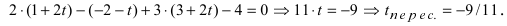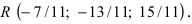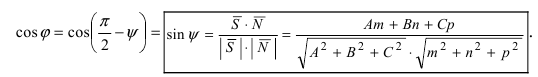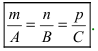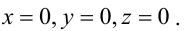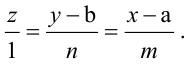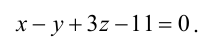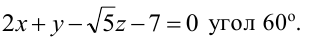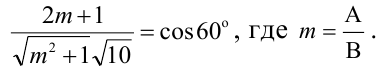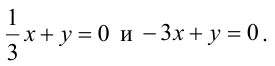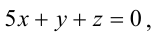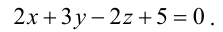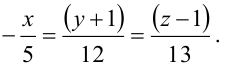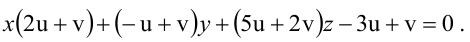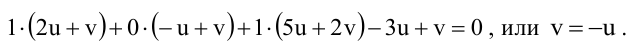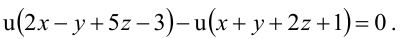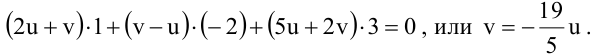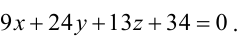Что значит что плоскость проходит через прямую

Плоскость в пространстве – необходимые сведения

Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.

Понятие плоскости и ее обозначения

Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.

В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.

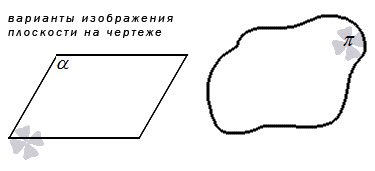
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.

Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.

Как могут располагаться плоскость и точка друг относительно друга

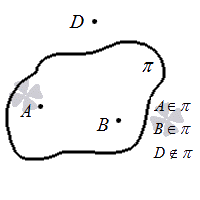
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:

В любой плоскости есть точки.

Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.

Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.

Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:

Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.

Графически последнюю аксиому можно представить так:

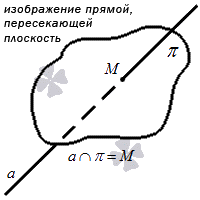
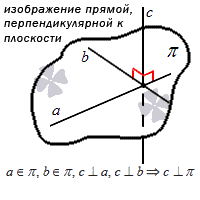
Варианты взаимного расположения прямой и плоскости

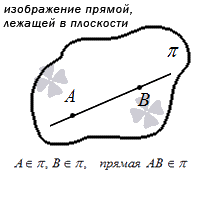
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:

Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.

Графически этот вариант расположения выглядит так:

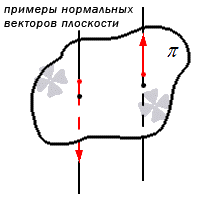
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.

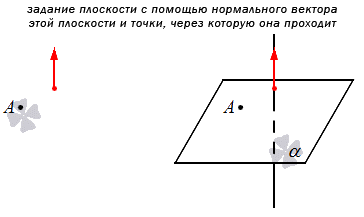
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.

Примеры нормальных векторов плоскости показаны на рисунке:

Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.

Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.

Варианты расположения двух плоскостей друг относительно друга

1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.

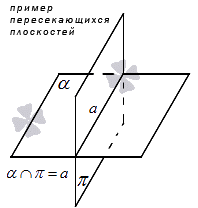
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:

Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.

На графике это будет выглядеть так:

В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.

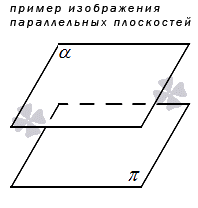
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.

Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.

Как задать плоскость в пространстве

В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.

1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.

Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:

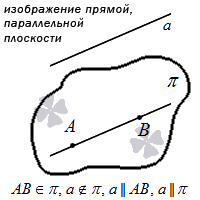
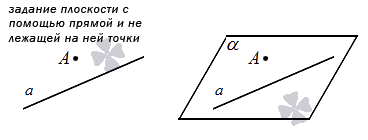
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:

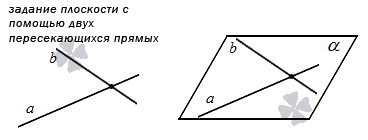
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:

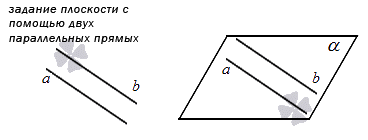
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.

На рисунке этот способ будет выглядеть так:

Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:

Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.

Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).

Вспомним одну теорему, изученную в рамках курса по геометрии:

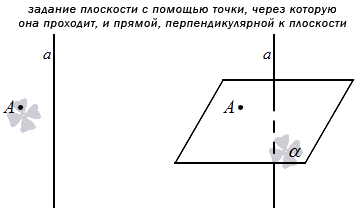
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.

Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.

Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.

Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.

Источник

Плоскость и прямая в пространстве с примерами решения

Содержание:

Плоскость в пространстве

Общее уравнение плоскости

Определение: Уравнение вида

Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.

Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.

Рассмотрим частные случаи приведенного уравнения:

1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36).

Рис. 36. Плоскость, проходящая через начало координат.

2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37).

Рис. 37. Плоскость, проходящая параллельно оси аппликат.

Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.

Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.

4. — плоскость проходит через точку параллельно плоскости (Pис. 39).

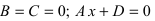
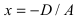
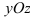
Рис. 39. Плоскость, проходящая параллельно координатной плоскости

Рис. 40. Координатная плоскость .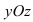

Другие уравнения плоскости

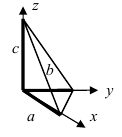
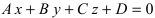
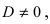
1. Уравнение плоскости в отрезках. Пусть в уравнении коэффициент тогда выполним следующие преобразования

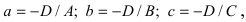
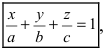
Введем следующие обозначения тогда уравнение примет вид которое называется уравнением плоскости в отрезках. Найдем точки пересечения плоскости с координатными осями:

Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41):

Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.

Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.

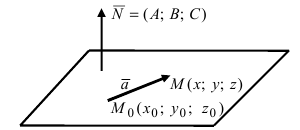
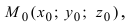
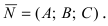
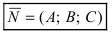
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка через которую проходит плоскость перпендикулярно к заданному вектору ОЗ. Вектор называется нормальным вектором плоскости, если он перпендикулярен любой паре неколлинеарных векторов, лежащих на плоскости.

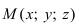
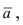
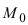
Возьмем на плоскости произвольную точку и образуем вектор соединяющий точку с точкой М (Рис. 42). Тогда

Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.

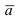
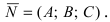
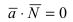
В силу того, вектор лежит в плоскости, то он перпендикулярен нормальному вектору Используя условие перпендикулярности векторов в проекциях перемножаемых векторов, получим уравнение плоскости, проходящая через заданную точку перпендикулярно к нормальному вектору:

Пример:

Составить уравнение плоскости, проходящей через т. 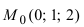параллельно плоскости

Решение:

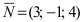
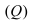
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости (см. коэффициенты при переменных величинах х, у и z в уравнении плоскости ) перпендикулярен к искомой плоскости и может быть взят в качестве нормального вектора этой плоскости. Используя уравнение плоскости, проходящей через заданную точку перпендикулярно к данному вектору, получаем:

Пример:

Решение:

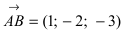
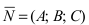
Построим на искомой плоскости вектор и вычислим нормальный вектор как векторное произведение векторов

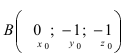
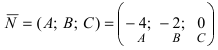
Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору имеет вид:

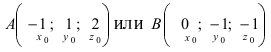
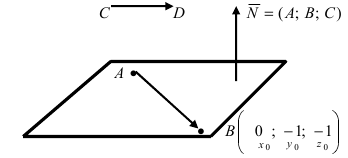
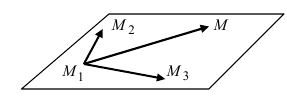
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек брать как точку, через которую проходит искомая плоскость.

3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 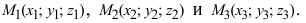Возьмем произвольную точку плоскости М(х; у; z) и образуем векторы

Рис. 43. Плоскость, проходящая через три заданные точки.

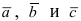
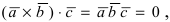
Вектора компланарные, используя условие компланарности векторов получим уравнение плоскости, проходящей через 3 известные точки:

Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.

Пример:

Составить уравнение плоскости, проходящей через три заданные точки

Решение:

Основные задачи о плоскости в пространстве

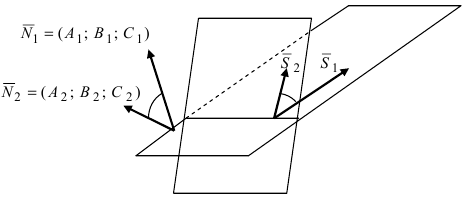
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 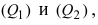которые имеют нормальные векторы

Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 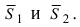Меньший угол между этими векторами определяет угол между плоскостями (Рис.44):

Рис.44. Угол между плоскостями.

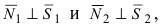
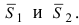
В силу того, что то угол между нормальными векторами равен углу между векторами Из векторной алгебры известно, что угол между векторами определяется формулой:

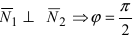
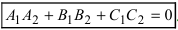
Следствие: Если плоскости перпендикулярны (), то условием перпендикулярности плоскостей является равенство: .

Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей:

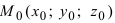
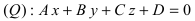
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки до заданной плоскости определяется по формуле:

Пример:

На каком расстоянии от плоскости 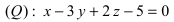находится точка

Решение:

Воспользуемся приведенной формулой:

Прямая в пространстве

Общее уравнение прямой

Прямая в пространстве может быть задана как пересечение двух плоскостей:

Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.

Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 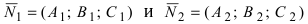были неколлинеарными, т.е. выполняется одно из неравенств:

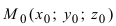
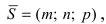
Пусть прямая проходит через точку параллельно вектору который называется направляющим вектором прямой (см. Лекцию Ле 7), тогда ее уравнение называется каноническим и имеет вид:

Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Пример:

Как расположена прямая 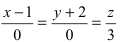относительно координатных осей.

Решение:

Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 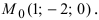Приравняв каждую дробь уравнения (2) параметру t, получим параметрическое уравнение прямой:

Пример:

Записать уравнение прямой 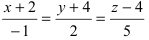в параметрическом виде.

Решение:

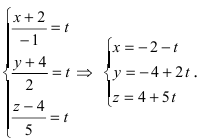
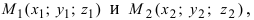
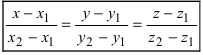
Приравняем каждую дробь к параметру t: Если прямая проходит через две известные точки то ее уравнение имеет вид: и называется уравнением прямой, проходящей через две заданные точки.

Пример:

Решение:

Составим каноническое уравнение прямой линии, проходящей через точки

Перейдём к параметрическому уравнению или Составим каноническое уравнение прямой линии, проходящей через точки

Перейдём к параметрическому уравнению прямой

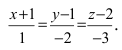
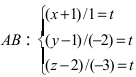
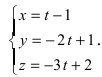
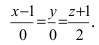
Основные задачи о прямой в пространстве

1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением 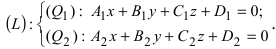Для того, чтобы перейти от этого уравнения прямой к каноническому, поступают следующим образом:

Пример:

Записать уравнение прямой 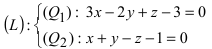в каноническом и параметрическом виде.

Решение:

Запишем каноническое 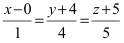и параметрическое уравнения прямой:

Угол между пересекающимися прямыми

Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 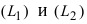имеют направляющие вектора

соответственно, то угол между прямыми определяется по формуле:

Следствие: Если прямые перпендикулярны (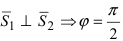), то условием перпендикулярности прямых является равенство:

Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых:

Координаты точки пересечения прямой и плоскости

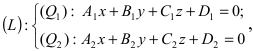
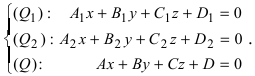
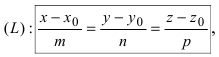
Пусть прямая (L) задана общим уравнением а плоскость (Q) уравнением Ax+By+Cz+D=0. Так как точка пересечения прямой и плоскости принадлежит одновременно обоим этим объектам, то ее координаты находят из системы уравнений: Если прямая (L) задана каноническим уравнением а плоскость (Q)

Рассмотрим возможные случаи:

Пример:

Найти координаты точки пересечения прямой (L), заданной уравнением 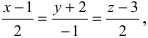и плоскости (Q): 2x-y+3z-4=0.

Решение:

Перепишем уравнение прямой (L) в параметрическом виде 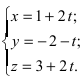Подставим найденные величины в уравнение плоскости (Q)? получим

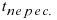
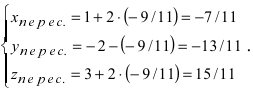
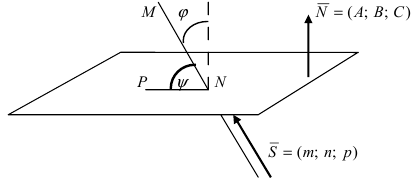
Найденное значение параметра подставим в параметрическое уравнение прямой Таким образом, прямая пересекает заданную плоскость в точке

Угол между прямой и плоскостью

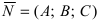
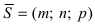
Пусть дана плоскость (Q) с нормальным вектором и пересекающая ее прямая (L) с направляющим вектором (Рис.45).

Рис. 45. Угол между прямой и плоскостью.

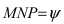
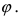
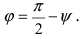
Угол является углом между прямой (L) и плоскостью (Q). Угол между нормальным вектором плоскости и прямой обозначим через Из рисунка видно, что Следовательно,

Следствие: Если прямая перпендикулярна плоскости (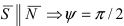), то условие перпендикулярности прямой и плоскости имеет вид:

Следствие: Если прямая параллельна плоскости (), то направляющий вектор прямой и нормальный вектор плоскости перпендикулярны (), следовательно, условие параллельности прямой и плоскости: .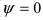

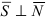
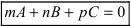
Плоскость и прямая в пространстве

Всякое уравнение первой степени относительно координат 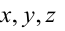задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.

Вектор 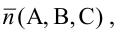ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты А, В, С одновременно не равны 0.

Особые случаи уравнения (3.1):

Уравнения координатных плоскостей:

Прямая в пространстве может быть задана:

Тогда прямая определяется уравнениями:

Уравнения (3.4) называются каноническими уравнениями прямой.

Вектор 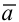называется направляющим вектором прямой.

Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 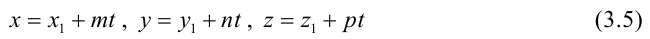Решая систему (3.2) как систему линейных уравнений относительно неизвестных х и у, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой.

От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

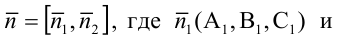
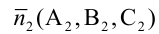
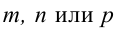
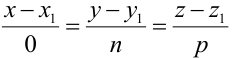
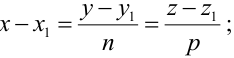
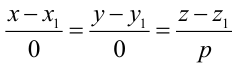
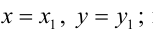
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор — нормальные векторы заданных плоскостей. Если один из знаменателей в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система равносильна системе такая прямая перпендикулярна к оси Ох. Система равносильна системе прямая параллельна оси Oz.

Пример:

Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.

Решение:

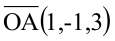
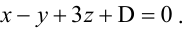
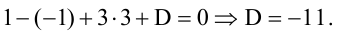
По условию задачи вектор является нормальным вектором плоскости, тогда ее уравнение можно записать в виде Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: Итак,

Пример:

Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью

Решение:

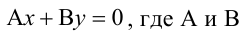
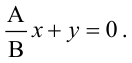
Плоскость, проходящая через ось Oz, задается уравнениемодновременно не обращаются в нуль. Пусть В не равно 0, По формуле косинуса угла В между двумя плоскостями

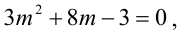
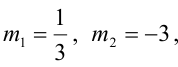
Решая квадратное уравнение находим его корни откуда получаем две плоскости

Пример:

Составьте канонические уравнения прямой:

Решение:

Канонические уравнения прямой имеют вид:

Канонические уравнения прямой имеют вид:

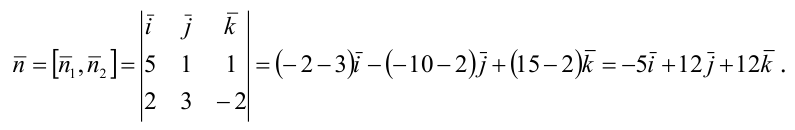
Пример:

В пучке, определяемом плоскостями 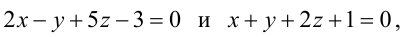найти две перпендикулярные плоскости, одна из которых проходит через точку М (1,0,1).

Решение:

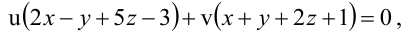
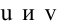
Уравнение пучка, определяемого данными плоскостями, имеет вид где не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом:

Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:

Тогда уравнение плоскости, содержащей М, найдем, подставив 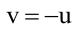в уравнение пучка:

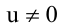
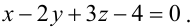
Т.к. и (иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей:

Значит, уравнение второй плоскости имеет вид: 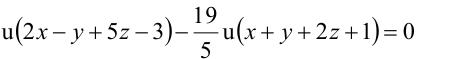или

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник