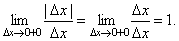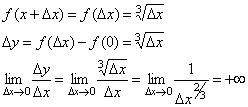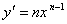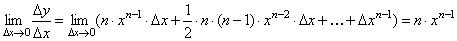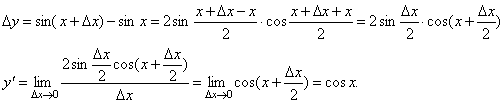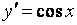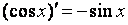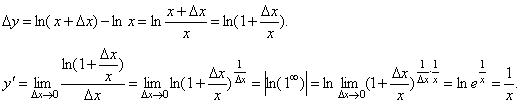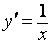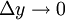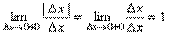Что значит что функция непрерывно дифференцируема

Непрерывность дифференцируемой функции

Функция y = f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения 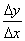существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y = f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

Таким образом, из дифференцируемости функции следует ее непрерывность.

,

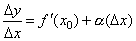
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

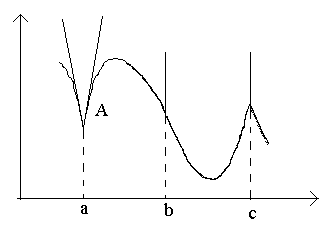
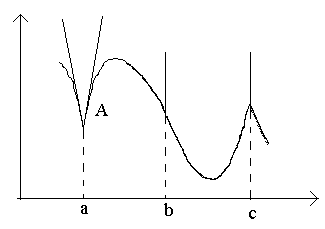
В точке a при Δx→0 отношение 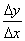не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками.

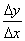
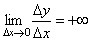
В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – «точка перегиба» c вертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.

Примеры.

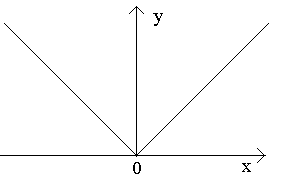
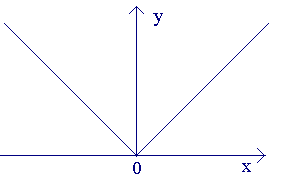
1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке x = 0, т.к. .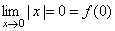

Покажем, что она не имеет производной в этой точке.

Т.о., отношение 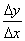при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная «кривая» не имеет определенной касательной (в этой точке их две).

2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x= 0.

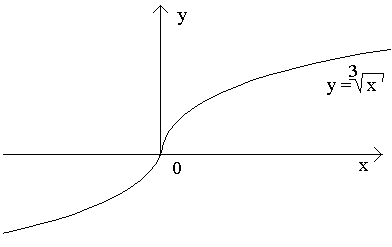
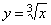
Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

Производные элементарных функций.

можно доказать, что

Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.

Найдем предел:

2. y= sin x. Вновь воспользуемся определением производной.

3. Аналогично можно показать, что

4. Рассмотрим функцию y= ln x.

5. Используя свойства логарифма можно показать, что

Источник

Что значит что функция непрерывно дифференцируема

3.2.3. дЙЖЖЕТЕОГЙТХЕНПУФШ ЖХОЛГЙК. оЕРТЕТЩЧОПУФШ ДЙЖЖЕТЕОГЙТХЕНПК ЖХОЛГЙЙ

еУМЙ ЖХОЛГЙС ДЙЖЖЕТЕОГЙТХЕНБ Ч ЛБЦДПК ФПЮЛЕ ОЕЛПФПТПЗП ПФТЕЪЛБ [ Б ; b ] ЙМЙ ЙОФЕТЧБМБ ( Б ; b ), ФП ЗПЧПТСФ, ЮФП ПОБ ДЙЖЖЕТЕОГЙТХЕНБ ОБ ПФТЕЪЛЕ [ Б ; b ] ЙМЙ УППФЧЕФУФЧЕООП Ч ЙОФЕТЧБМЕ ( Б ; b ).

уРТБЧЕДМЙЧБ УМЕДХАЭБС ФЕПТЕНБ, ХУФБОБЧМЙЧБАЭБС УЧСЪШ НЕЦДХ ДЙЖЖЕТЕОГЙТХЕНЩНЙ Й ОЕРТЕТЩЧОЩНЙ ЖХОЛГЙСНЙ.

фБЛЙН ПВТБЪПН, ЙЪ ДЙЖЖЕТЕОГЙТХЕНПУФЙ ЖХОЛГЙЙ УМЕДХЕФ ЕЕ ОЕРТЕТЩЧОПУФШ.

еУМЙ , ФП

ЗДЕ ВЕУЛПОЕЮОП НБМБС ЧЕМЙЮЙОБ, Ф.Е. ЧЕМЙЮЙОБ, УФТЕНСЭБСУС Л ОХМА РТЙ . оП ФПЗДБ

фБЛЙН ПВТБЪПН, Ч ФПЮЛБИ ТБЪТЩЧБ ЖХОЛГЙС ОЕ НПЦЕФ ЙНЕФШ РТПЙЪЧПДОПК. пВТБФОПЕ ХФЧЕТЦДЕОЙЕ ОЕЧЕТОП: УХЭЕУФЧХАФ ОЕРТЕТЩЧОЩЕ ЖХОЛГЙЙ, ЛПФПТЩЕ Ч ОЕЛПФПТЩИ ФПЮЛБИ ОЕ СЧМСАФУС ДЙЖЖЕТЕОГЙТХЕНЩНЙ (Ф.Е. ОЕ ЙНЕАФ Ч ЬФЙИ ФПЮЛБИ РТПЙЪЧПДОПК).

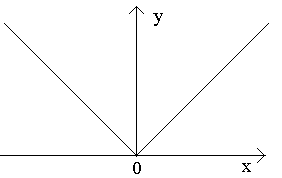
тБУУНПФТЙН ОБ ТЙУХОЛЕ ФПЮЛЙ Б, b, c.

ч ФПЮЛЕ b РТЙ ПФОПЫЕОЙЕ СЧМСЕФУС ЪОБЛПРПУФПСООПК ВЕУЛПОЕЮОП ВПМШЫПК ЧЕМЙЮЙОПК .

жХОЛГЙС ЙНЕЕФ ВЕУЛПОЕЮОХА РТПЙЪЧПДОХА. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ЧЕТФЙЛБМШОХА ЛБУБФЕМШОХА. фЙР ФПЮЛЙ – «ФПЮЛБ РЕТЕЗЙВБ» c ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК.

ч ФПЮЛЕ c ПДОПУФПТПООЙЕ РТПЙЪЧПДОЩЕ СЧМСАФУС ВЕУЛПОЕЮОП ВПМШЫЙНЙ ЧЕМЙЮЙОБНЙ ТБЪОЩИ ЪОБЛПЧ. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ДЧЕ УМЙЧЫЙЕУС ЧЕТФЙЛБМШОЩЕ ЛБУБФЕМШОЩЕ. фЙР – «ФПЮЛБ ЧПЪЧТБФБ» У ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК – ЮБУФОЩК УМХЮБК ХЗМПЧПК ФПЮЛЙ.

тБУУНПФТЙН ЖХОЛГЙА y=|x|.

ьФБ ЖХОЛГЙС ОЕРТЕТЩЧОБ Ч ФПЮЛЕ x = 0, Ф.Л. .

рПЛБЦЕН, ЮФП ПОБ ОЕ ЙНЕЕФ РТПЙЪЧПДОПК Ч ЬФПК ФПЮЛЕ.

оП ФПЗДБ РТЙ

б РТЙ > 0

ф.П., ПФОПЫЕОЙЕ РТЙ УРТБЧБ Й УМЕЧБ ЙНЕЕФ ТБЪМЙЮОЩЕ РТЕДЕМЩ, Б ЬФП ЪОБЮЙФ, ЮФП ПФОПЫЕОЙЕ РТЕДЕМБ ОЕ ЙНЕЕФ, Ф.Е. РТПЙЪЧПДОБС ЖХОЛГЙЙ y=|x| Ч ФПЮЛЕ x = 0 ОЕ УХЭЕУФЧХЕФ. зЕПНЕФТЙЮЕУЛЙ ЬФП ЪОБЮЙФ, ЮФП Ч ФПЮЛЕ x = 0 ДБООБС «ЛТЙЧБС» ОЕ ЙНЕЕФ ПРТЕДЕМЕООПК ЛБУБФЕМШОПК (Ч ЬФПК ФПЮЛЕ ЙИ ДЧЕ).

Источник

Непрерывная дифференцируемость

Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.

Содержание

Определения

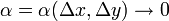
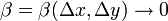
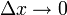
где и при ,

Свойства

Касательная прямая

Примеры

См. также

Ссылки

Полезное

Смотреть что такое «Непрерывная дифференцируемость» в других словарях:

Дифференцируемая функция — Дифференцируемая (в точке) функция это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является… … Википедия

Дифференциальное исчисление — раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 … Большая советская энциклопедия

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБЫКНОВЕННОЕ — уравнение, в к ром неизвестной является функция от одного независимого переменного, причем в это уравнение входят не только сама неизвестная функция, но и ее производные различных порядков. Термин дифференциальные уравнения был предложен Г.… … Математическая энциклопедия

ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ В БАНАХОВОМ ПРОСТРАНСТВЕ — уравнение вида где A0(t), A1(t).при каждом t линейные операторы в банаховом пространстве Е, g(t) заданная, a u(t) искомая функции со значениями в Е;производная ипонимается как предел по норме Еразностного отношения. 1. Линейное дифференциальное… … Математическая энциклопедия

Приближение функций комплексного переменного — раздел комплексного анализа, изучающий вопросы приближённого представления (аппроксимации) функций комплексного переменного посредством аналитических функций (См. Аналитические функции) специальных классов. Центральная проблематика… … Большая советская энциклопедия

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

Источник

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ.

Функция y=f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

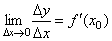
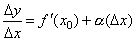
Доказательство. Если , то ,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Таким образом,из дифференцируемости функции следует ее непрерывность.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

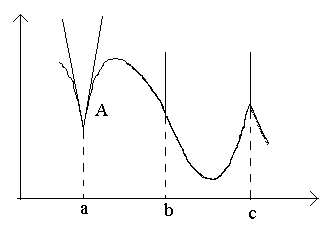
В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками. В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – «точка перегиба» c вертикальной касательной.

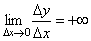
В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.

Пример.

Покажем, что она не имеет производной в этой точке.

Т.о., отношение при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная «кривая» не имеет определенной касательной (в этой точке их две).

Источник

Непрерывно дифференцируемая функция

Непрерывно дифференцируемая функция

Случай функций одной переменной

В этом случае непрерывно дифференцируемая функция есть дифференцируемая функция, у которой первая производная непрерывна. Такие функции часто называют гладкими функциями.

Рассматривают также дважды непрерывно дифференцируемые функции — функции имеющие непрерывную вторую производную.

Аналогично можно ввести понятие n раз непрерывно дифференцируемых функций.

Случай функций многих переменной

В этом случае понятие непрерывно дифференцируемой функции может рассматриваться в двух видах:

Приближение непрерывно-дифференцируемых функций аналитическими

Полезное

Смотреть что такое «Непрерывно дифференцируемая функция» в других словарях:

Дифференцируемая функция — [differentiable function] функция, имеющая в каждой точке области, на которой она определена, полный дифференциал, а в случае функции одного переменного производную[1]. Если функция f(x) дифференцируема в точке x, то она и непрерывна в этой точке … Экономико-математический словарь

дифференцируемая функция — Функция, имеющая в каждой точке области, на которой она определена, полный дифференциал, а в случае функции одного переменного производную[1]. Если функция f(x) дифференцируема в точке x, то она и непрерывна в этой точке. Если она дифференцируема … Справочник технического переводчика

Вогнутая функция — Функция(её график выделен синим) выпукла тогда и только тогда когда область над её графиком (закрашено зеленым) является выпуклым множеством. В математике функция называется выпуклой (или выпуклой вниз) на некотором интервале (в общем случае на… … Википедия

Выпуклая функция — Выпуклая функция, её график выделен синим и надграфик закрашен зеленым. Выпуклая функция функция, у которой надграфик является выпуклым множеством … Википедия

Гладкая функция — или непрерывно дифференцируемая функция это функция, имеющая непрерывную производную на всём множестве определения. Основные сведения Рассматривают также гладкие функции высших порядков, а именно, функция с порядком гладкости имеет… … Википедия

ЛЯПУНОВА ФУНКЦИЯ — функция, определяемая следующим образов. Пусть х 0 неподвижная точка системы дифференциальных уравнений (т. е. ), где отображение непрерывной непрерывно дифференцируемо по х(здесь U нек рая окрестность точки х 0 в ); в координатах эта система… … Математическая энциклопедия

ОБОБЩЁННАЯ ФУНКЦИЯ — матем. понятие … Физическая энциклопедия

АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия

Источник