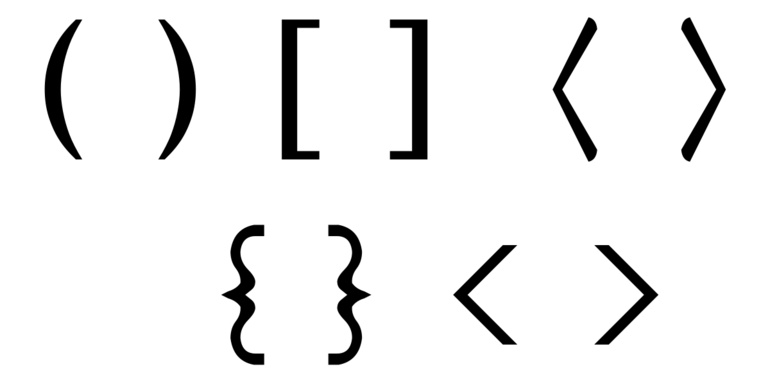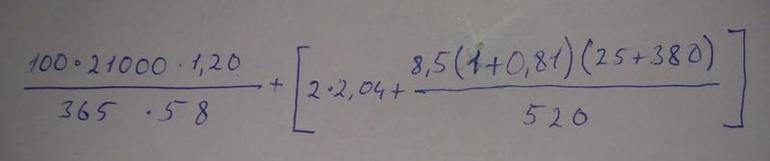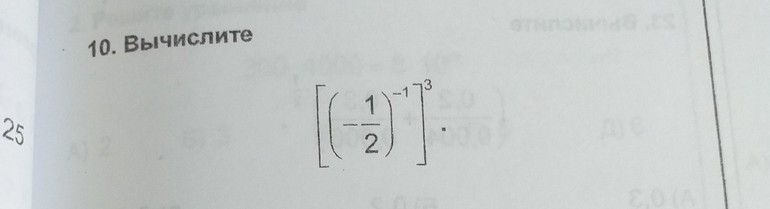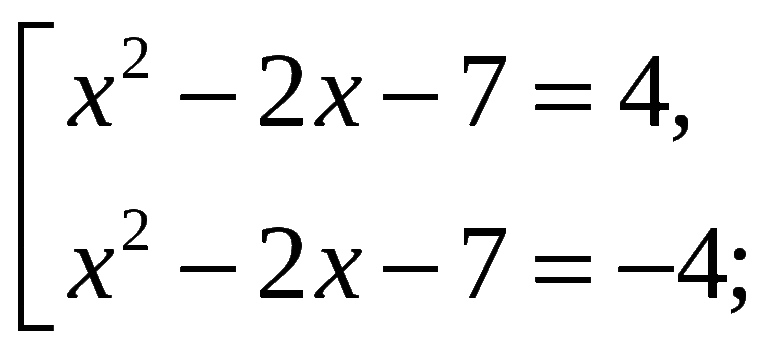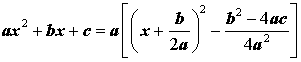Что означают квадратные скобки в формуле математика

Общая характеристика

Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.

Значение и разновидности

Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.

В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.

Разновидности:

Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.

В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.

Основные цели квадратной скобки в математике:

Другие варианты расчета:

Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.

Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.

Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.

На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.

Одинарные или двойные выражения

Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.

В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.

Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.

По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.

В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.

В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).

Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0

Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.

Прочие знаки

Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.

Удобство записи системы уравнений

Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.

Источник

Скобки в математике

Вы будете перенаправлены на Автор24

Скобки в математике играют очень важную роль: с помощью них задаётся порядок действий с выражением, обозначаются границы промежутков и необходимость выполнения какого-либо действия над выражением. Также с помощью скобок обозначаются вектора и матрицы и действия с множествами.

Использование круглых скобок в математике

Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.

Первое применение.

С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.

В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.

Второе применение.

Третье применение.

Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.

$(x+2)^2; \int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$

Четвёртое применение.

Пятое применение.

Готовые работы на аналогичную тему

Пятое применение.

Квадратные скобки в математике

Что же означают квадратные скобки в математике и для чего они используются?

Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.

Первое применение.

Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.

Второе применение.

Третье применение.

С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.

$\left [ \begin x +32=2y \\ y^2-12=0 \\ \end\right.$

Фигурная скобка в математике

Первое применение.

С помощью символа фигурной скобки обозначают систему уравнений, решением которой являются корни, подходящие для всех уравнений, включённых в систему.

Второе применение.

Третье применение.

Треугольные скобки

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 06 03 2021

Источник

Что означают квадратные скобки в математике?

Квадратные скобки ([ ])- специальный символ, который используют не только в математике, но и в программировании, в русском языке, в химических науках и даже при изображении смайликов. Чаще всего они всегда парные и дополняют друг друга.

В математике в квадратные скобки заключаются выражения, если они уже содержат скобки. В таких случаях кроме круглых скобок применяют квадратные. Сначала выполняются действия в круглых, а затем внутри квадратных скобках.

Кроме того, квадратные скобки в математике используются для:

В математике так обозначают векторные значения,когда закрытые сегменты,коммутатор,антикоммутатор,при записи матриц,при объединении совокупности уравнений и неравенств,операция целого взятия числа,когда нужно обозначить в задании приоритета операций(аналогично круглым) в качестве скобок «второго уровня».

Ответ bezdelnick опоздал лет на 40. Еще когда я в школе учился, уже отказались от внешних квадратных скобок. Только круглые!

Хотя так писать действительно удобнее, и меньше шансов запутаться в скобках, если пример достаточно сложный.

Еще квадратные скобки используются для обозначения определителя матрицы. Но ты, скорее всего, еще не знаешь этой темы.

Я просто напишу, что это такое, а более подробно ты изучишь в институте.

На подчеркивания не обращай внимания, они здесь вместо пробелов. Сайт пробелы съедает.

Также квадратными скобками обозначаются закрытые множества, в которые входят концы отрезков.

И наконец, квадратной скобкой слева от нескольких уравнений обозначается их совокупность.

Это когда должно выполняться хотя бы одно из уравнений, любое.

У этой совокупности 3 решения: 2 у первого уравнения и 1 у второго.

В отличие от системы, которая обозначается фигурной скобкой. В системе должны выполняться все уравнения сразу.

У этой системы решений нет, потому что решения первого уравнения не подходят ко второму.

Квадратные скобки выполняют широкий спектр задач и могут использоваться не только в математике, но и в русском языке.

В математике данные скобки могут использоваться наравне с круглыми в уравнениях, чтобы можно было разграничить действия и не путаться.

Кроме того, квадратные скобки активно используются в уравнениях с векторами.

Квадратные скобки [ ] в математике обозначают приоритет второго уровня выполнения действий, указанных в этих скобках. Приоритет первого уровня обозначают круглыми скобками ( ), которые должны быть внутри квадратных. Например[(7+16)*5]=23*5=115. Но они могут применяться и для других целей.

В математике применяются не только круглые скобки, но и квадратные.

Квадратные скобки могут обозначать следующее:

-операцию взятия целой части числа

-для задания приоритета операций

-используются как альтернатива при записи матриц и векторов

-одинарная квадратная скобка объединяет совокупность уравнений или неравенств.

В математике есть не только круглые, но и квадратные скобки, которые применимы в таких случаях как:

1) В случае когда проводится взятие целой части числа в скобки уместно писать квадратные;

2) Если речь идёт о произведении векторов;

3) Для выделения приоритетов в примерах и уравнениях;

4) Квадратные скобки могут быть использованы во время записей векторов им матриц как альтернатива;

5) также квадратная скобка объединяет в себе совокупности уравнений или же неравенств.

Помимо привычных круглых скобок в математике используют и квадратные скобки. В частности, квадратные скобки используют к качестве скобок второго уровня. То есть, если уравнение уже содержит круглые скобки (одну пару или больше), а уравнение нужно еще раз взять в скобки, то уравнение берут в квадратные, чтобы было легче воспринять большое количество скобок. В таком уравнении сначала решают выражение в круглых скобках, а затем уже в квадратных.

Квадратные скобки, как и круглые, часто применяются в математики при операции взятия целой части числа.

Иногда уравнения берут в скобки не только круглые, но и квадратные, последние из которых являются скобками второго уровня: [(5+1)·8]².

Также квадратными скобками обозначают в математике векторное произведение векторов:

Квадратные скобки в математике, могут обозначать следующее:

Могу посоветовать сайт, которым пользуемся мы, когда ищем ответы по математике. Он называется слово, потом точка, потом домен ws (а не ru).

Там постранично отсканирован решебник, просто и понятно изложено. Вот выдержка именно из него:

Там есть и другие решебники, пригодятся ребенку позже.

Есть еще математикус.ру.

Есть сайт алленг.ру, там можно помимо готовых домашних заданий найти учебники (в том числе и для высшего и средне-профессионального образования), их количество постоянно пополняется.

Можно поискать в книжных магазинах.

Если раньше все школы нашей необъятной Родины учились по единому учебнику, то в настоящее время учебников по одному и тому же предмету развелось вагон и маленькая тележка.

Ответы по математике,можно купить решебник в книжном магазине, либо скачать с интернета, либо посмотреть решебники онлайн. Главное чтобы автор учебника, совпал с ответами решебника. Поэтому сначала следует посмотреть создателей учебника.

Математика на экономических специальностях не слишком сложная, в основном статистика.

Можно попробовать пересчитать. Хотя бы приблизительно.

Источник

Знак примерно (приблизительно) на клавиатуре: как поставить на компьютере или ноутбуке?

Общая характеристика

Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.

Значение и разновидности

Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.

В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.

Разновидности:

Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.

В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.

Основные цели квадратной скобки в математике:

Другие варианты расчета:

Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.

Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.

Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.

На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.

Одинарные или двойные выражения

Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.

В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.

Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.

По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.

В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.

В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).

Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0

Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.

Фигурные скобки

В вики-разметке двойные фигурные скобки применяются для шаблонов.

Использование круглых скобок в математике

Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.

Первое применение.

С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.

В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.

Готовые работы на аналогичную тему

Второе применение.

Третье применение.

Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.

$(x+2)^2; int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$

Четвёртое применение.

Пятое применение.

Пятое применение.

Угловые скобки

В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как (кет-вектор) и (бра-вектор), их скалярное произведение как матричный элемент оператора А в определённом базисе как

Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например, — среднее значение по времени от величины f.

В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте — .

Второй способ

Если вам нужны исключительно две волнистые черты, их тоже можно поставить, но способ чуть более долгий.

На клавиатуре своего устройства нажмите Win+R.

Появится окно «Выполнить». Добавьте команду charmap.exe, нажмите ОК.

Запущена таблица символов Windows.

Выбираете шрифт Arial, затем в списке находите символ приблизительно (примерно), нажимаете на него левой клавишей мыши, а затем по очереди — на кнопки «Выбрать» и «Копировать».

Теперь вставляете символ в определенное место вашего текста.

Вставка символа без клавиатуры

В Word для вставки символа приблизительно равно можно воспользоваться функцией вставки. На вкладке «Вставка» открываем окно «Другие символы».

Выбираем шрифт «обычный текст» и набор «математические операторы». В первых рядах будет нужный знак.

Конвертация кода в знак

Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».

Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:

Оба варианта работают в Word, Excel и других офисных программах.

Первый способ

Скажем сразу — для этого способа мы будем использовать символ тильда в виде одной волнистой черты, в то время как в знаке приблизительно черты две. Тем менее, тильду часто используют в качестве символа примерно, так что проблем быть не должно.

Используйте англоязычную раскладку. Если используется русскоязычная, переключите ее, нажав Shift+Ctrl:

Или используйте языковую иконку, которая находится на панели задач:

Теперь найдите символ тильды (слева от цифры 1, часто на этой же клавише можно увидеть букву ё).

Однако если нажать на указанную клавишу, вы увидите совсем другой символ, поэтому предварительно нажмите на Shift и, удерживая его, нажмите на клавишу тильда, после чего отпустите Shift.

Что у вас должно получиться:

Квадратные скобки в математике

Что же означают квадратные скобки в математике и для чего они используются?

Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.

Первое применение.

Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.

$[(5+2) cdot 2] cdot(25-3+(-5))$

Второе применение.

Третье применение.

С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.

$left [ begin x +32=2y \ y^2-12=0 \ endright.$

Круглые скобки

Используются в математике для задания приоритета математических и логических операций. Например, (2+3)·4 означает, что надо сначала сложить 2 и 3, а затем сумму умножить на 4; аналогично выражение означает, что сначала выполняется логическое сложение а затем — логическое умножение Наряду с квадратными скобками используются также для записи компонент векторов :

для записи биномиальных коэффициентов :

Круглые скобки в математике используются также для выделения аргументов функции: для обозначения открытого сегмента и в некоторых других контекстах. Иногда круглыми скобками обозначается скалярное произведение векторов:

(здесь приведены три различных варианта написания, встречающиеся в литературе) и смешанное (тройное скалярное) произведение :

Скобки (обычно круглые, как в этом предложении) употребляются в качестве знаков препинания в естественных языках.

Источник