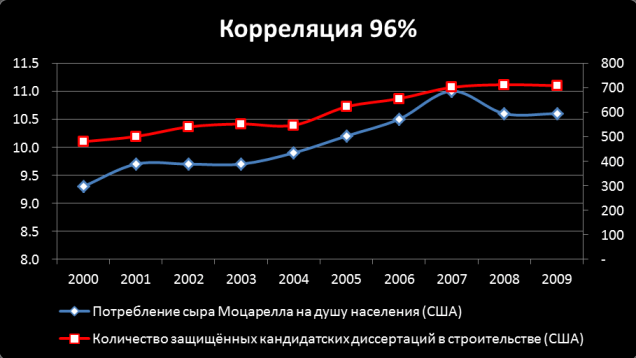
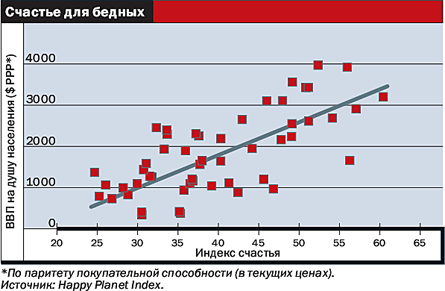
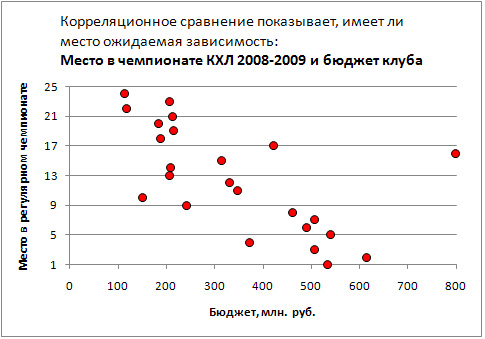
Что означает термин корреляция
Корреляция
Смотреть что такое «Корреляция» в других словарях:
корреляция — КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio соотношение) термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений. Большинство психологических… … Большая психологическая энциклопедия
КОРРЕЛЯЦИЯ — [лат. correlatio] взаимная связь, соотношение предметов или понятий. Словарь иностранных слов. Комлев Н.Г., 2006. КОРРЕЛЯЦИЯ новолатинск. от relata. Взаимное отношение, например, существующее между опекуном и опекаемым. Объяснение 25000… … Словарь иностранных слов русского языка
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) … Словарь синонимов
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов … Большой Энциклопедический словарь
КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… … Философская энциклопедия
корреляция — и, ж. corrélation f., нем. Korrelation <лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… … Исторический словарь галлицизмов русского языка
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
Значение слова «корреляция»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Математической мерой корреляции двух случайных величин служит корреляционное отношение
либо коэффициент корреляции
). В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Впервые в научный оборот термин корреляция ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.
КОРРЕЛЯ’ЦИЯ, и, ж. [латин. correlatio] (науч.). 1. Соотношение, взаимная зависимость сопоставляемых понятий (филос.). 2. Взаимная связь явлений, находящихся в известной зависимости друг от друга. Рост безработицы и количество уголовных преступлений находятся в прямой корреляции друг к другу.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
корреля́ция
1. матем. статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми) ◆ Высок коэффициент парной корреляции между переменными x₁ и x₃ (коэффициент корреляции 0,9), что показывает их тесную корреляционную взаимосвязь. К. М. Семенович, Б. П. Чупрынов, «Математика для экономистов: Учебное пособие», 2015 г. (цитата из библиотеки Google Книги) ◆ Если, когда увеличивается одно значение, то в большинстве случаев увеличивается и второе, корреляция положительная, а если одно значение уменьшается при увеличении второго, то тут корреляция уже отрицательная, или обратная. Пример отрицательной корреляции — график, показывающий, как соотносится температура воздуха с высотой над уровнем моря. Чем выше на гору вы забираетесь, тем холоднее воздух. М. Эскью, Р. Истуэй, «Математика с удовольствием!», 2017 г. (цитата из библиотеки Google Книги)
2. психол. взаимное соотношение, соответствие понятий и явлений ◆ Всё большее количество фактов поддерживают теорию, согласно которой существует корреляция между Я-концепцией и успеваемостью в школе. У успешных учеников более развитое чувство достоинства, и они в какой-то мере лучше относятся к себе (Garzarelli, Ever art, and Lester, 1993). Тем не менее эта связь обратима. Те, у кого высокая самооценка, лучше учатся в школе, а те, кто хорошо учится в школе, имеют более высокую самооценку… Ф. Райс, «Психология подросткового и юношеского возраста», 2010 г. (цитата из библиотеки Google Книги) ◆ Положительные, но умеренные по величине корреляции между учебными оценками и результатами тестирования не позволяли исследователям однозначно утверждать, что интеллект детерминирует успешность обучения. В. Н. Дружинин, «Психология общих способностей. 3-е изд.», 2013 г. (цитата из библиотеки Google Книги) ◆ «Корреляция» в прямом переводе означает соотношение. Если изменение одной переменной сопровождается изменением другой, то говорят о корреляции этих переменных. Наличие корреляции двух переменных не является свидетельством наличия причинно-следственных зависимостей между ними, но даёт возможность выдвинуть такую гипотезу. Отсутствие корреляции позволяет опровергнуть гипотезу о причинно-следственной связи переменных. М. Коновалова, «Экспериментальная психология: конспект лекций», 2017 г. (цитата из библиотеки Google Книги)
3. книжн. взаимная связь явлений, соотношение ◆ Корреляция между атмосферным давлением и влажностью воздуха. ◆ Количество уголовных преступлений и рост безработицы находятся друг к другу в прямой корреляции.
4. биол. взаимная согласованность функций частей и строения и животного или растения, которая поддерживает постоянство его внутренней среды и является следствием приспособления организма к условиям его существования ◆ Закон корреляции (Ж. Кювье, 1793): в организме, как целостной системе, все его части соответствуют друг другу как по строению, так и по выполняемым функциям. Р. Е. Михайловна, Ш. Т. Матвеевна, Ш. Л. Алексеевна, «Биология (Учебник)», 2016 г. (цитата из библиотеки Google Книги)
5. лог. отношение между двумя одинаковыми по форме связями; в случае, если одна связь становится изоморфной другой, тогда это — корреляция, а само закономерное структурное изменение – коррелятор
Что означает понятие корреляции простыми словами?
Все в мире взаимосвязано. Каждый человек на уровне интуиции пытается найти взаимосвязи между явлениями, чтобы иметь возможность влиять на них и управлять ними. Понятие, которое отражает эту взаимосвязь, называется корреляцией. Что она означает простыми словами?
Понятие корреляции
Корреляция (от латинского «correlatio» – соотношение, взаимосвязь) – математический термин, который означает меру статистической вероятностной зависимости между случайными величинами (переменными).
Пример: возьмем два вида взаимосвязи:
Примерами взаимосвязи между природными явлениями являются: цепочка питания в природе, организм человека, который состоит из систем органов, взаимосвязанных между собой и функционирующих как единое целое.
Каждый день мы сталкиваемся с корреляционной зависимостью в повседневной жизни: между погодой и хорошим настроением, правильной формулировкой целей и их достижением, положительным настроем и везением, ощущением счастья и финансовым благополучием. Но мы ищем связи, опираясь не на математические расчеты, а на мифы, интуицию, суеверия, досужие домыслы. Эти явления очень сложно перевести на математический язык, выразить в цифрах, измерить. Другое дело, когда мы анализируем явления, которые можно просчитать, представить в виде цифр. В таком случае мы можем определить корреляцию с помощью коэффициента корреляции (r), отражающего силу, степень, тесноту и направление корреляционной связи между случайными переменными.
Сильная корреляция между случайными величинами – свидетельство наличия некоторой статистической связи конкретно между этими явлениями, но эта связь не может переноситься на эти же явления, но для другой ситуации. Часто исследователи, получив в расчетах значительную корреляцию между двумя переменными, основываясь на простоте корреляционного анализа, делают ложные интуитивные предположения о существовании причинно-следственных взаимосвязей между признаками, забывая о том, что коэффициент корреляции носит вероятностный характер.
Пример: количество травмированных во время гололеда и число ДТП среди автотранспорта. Эти величины будут коррелировать между собой, хотя они абсолютно не взаимосвязаны между собой, а имеют только связь с общей причиной этих случайных событий – гололедицей. Если же анализ не выявил корреляционной взаимосвязи между явлениями, это еще не является свидетельством отсутствия зависимости между ними, которая может быть сложной нелинейной, не выявляющейся с помощью корреляционных расчетов.
Первым, кто ввел в научный оборот понятие корреляции, был французский палеонтолог Жорж Кювье. Он в XVIII веке вывел закон корреляции частей и органов живых организмов, благодаря которому появилась возможность восстанавливать по найденным частям тела (останкам) облик всего ископаемого существа, животного. В статистике термин корреляции впервые применил в 1886 году английский ученый Френсис Гальтон. Но он не смог вывести точную формулу для расчета коэффициента корреляции, но это сделал его студент – известнейший математик и биолог Карл Пирсон.
Виды корреляции
По значимости – высокозначимая, значимая и незначимая.
Значение слова корреляция
Словарь Ушакова
коррел я ция, корреляции, жен. (лат. correlatio) (научн.).
1. Соотношение, взаимная зависимость сопоставляемых понятий (филос.).
2. Взаимная связь явлений, находящихся в известной зависимости друг от друга. Рост безработицы и количество уголовных преступлений находятся в прямой корреляции друг к другу.
Современный экономический словарь. 1999
в экономической статистике: понятие, отражающее наличие связи между явлениями, процессами и характеризующими их величинами.
Словарь лингвистических терминов
(средневековолат. correlatio — соотношение). Взаимная зависимость, соотносительность двух или более языковых единиц.
Начала Современного Естествознания. Тезаурус
(от лат. correlatio — соотношение)
1) взаимное соотношение предметов, понятий, взаимозависимость;
2) (в математике) понятие, которым отмечают связь между явлениями, если одно из них входит в число причин, определяющих другие, или если имеются общие причины, воздействующие на эти явления;
3) (в биологии) взаимная приспособленность, согласованность, соотнесенность всех органов, всех частей тела друг с другом, так что вообще изменение одного органа или одной части тела влечет за собой изменение остальных. Подобная корреляция имеет место в области психологии и социологии. В биологию термин «корреляция» ввел французский биолог Жорж Кювье.
Антропологический толковый словарь
взаимосвяз (взаимовлияние) двух данных единиц друг на друга (например, корреляция между признаками).
Толковый переводоведческий словарь
1. Взаимная обусловленность, семиологическая зависимость двух или более единиц языка.
Вестминстерский словарь теологических терминов
♦ ( ENG correlation)
соотношение одного к одному.
Тезаурус русской деловой лексики
Syn: соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность
Энциклопедический словарь
Словарь Ожегова
КОРРЕЛЯЦИЯ, и, ж. (книжн.). Взаимная связь, соотношение.
| прил. корреляционный, ая, ое.
Словарь Ефремовой
ж.
Взаимная связь, соотношение предметов, явлений или понятий.
Энциклопедия Брокгауза и Ефрона
(лат. correlatio) — термин, предложенный покойным профессором казанского университета Н. В. Крушевским (см.) для обозначения таких звуковых чередований (в области одного и того же языка), которые не обусловливаются более, в данный момент жизни языка, никакими реальными причинами и представляют собой просто остаток или след некогда действовавшего звукового процесса. Члены такого чередования (коррелятивы) уже утратили известную необходимую связь, соединявшую их между собой, и находятся в отношении простого «сосуществования» или «соотношения». Так, напр., гласные о и у в словах муха и мошка в настоящее время суть коррелятивы, так как их чередование теперь ничем не обусловлено. Таково же взаимное отношение звуков е, о, е в формах: реку, про-рок, речь и т. д. См. также Дивергенция (см.). Ср. Крушевский, «К вопросу о гуне» («Р. Филол. Вест.», 1887, кн. I, и отдельно: Введение); его же, «Ueber die Lautabwechslung» (Казань, 1881); его же, «Очерк науки о языке» (Казань, 1883); Бодуэн де-Куртенэ, «Некоторые отделы сравн. грамматики слав. яз.» («Р. Филол. Вест.», 1881, кн. 2); его же, «Pr ó ba teorji alternacyj fonetyczuych» (Краков, 1894, ч. I).
Корреляции в дипломных работах по психологии
Термин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии.
В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии.
Что такое корреляция
Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.
Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».
Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).
Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?
Правильно, между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.
В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.
Численное выражение корреляционной зависимости
Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.
Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:
Прямая и обратная
Сильная и слабая
Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.
Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.
Испытуемый
Успеваемость (баллы)
Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.
Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость между интеллектом и успеваемостью равна 1.
Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).
Испытуемый
Успех в общении с противоположным полом (баллы)
Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.
А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.
Испытуемый
Длина прыжка с места (м)
Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.
Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:
Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях.
Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение).
Корреляционный анализ в психологии
Корреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли?
В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения.
Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:
Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:
Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места.
Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи.
Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола.
Коэффициенты Пирсона и Спирмена
Рассмотрим два метода расчета.
Коэффициент Пирсона – это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:
Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:
В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат.
В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат.
Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных.
Как рассчитать коэффициент корреляции
Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.
Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.
Расчет с помощью электронных таблиц Microsoft Excel
Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.
Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».
Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.
В таблицах Excel реализована формула расчета только коэффициента Пирсона.
Расчет с помощью программы STATISTICA
Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.
Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.
Использование корреляционного анализа в дипломных работах по психологии (пример)
Большинство тем выпускных квалификационных работ по психологии (дипломов, курсовых, магистерских) предполагают проведение корреляционного исследования (остальные связаны с выявлением различий психологических показателей в разных группах).
Сам термин «корреляция» в названиях тем звучит редко – он скрывается за следующими формулировками:
Рассмотрим кратко этапы его проведения при написании дипломной работы по психологии на тему: «Взаимосвязь личностной тревожности и агрессивности у подростков».
1. Для расчета необходимы сырые данные, в качестве которых обычно выступают результаты тестирования испытуемых. Они заносятся в сводную таблицу и помещаются в приложение. Эта таблица устроена следующим образом: