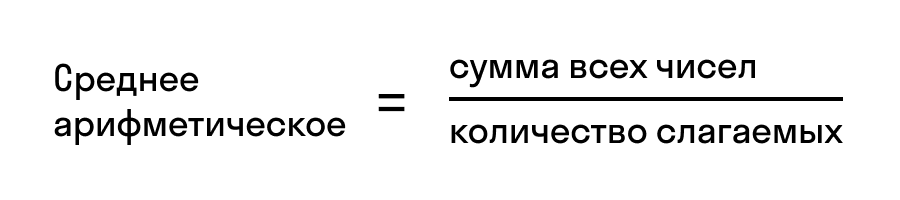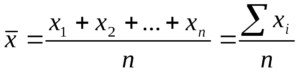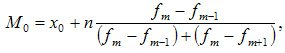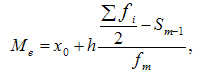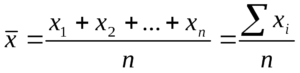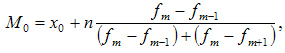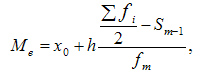Что означает среднее значение

3 простых формулы, чтобы посчитать среднее арифметическое

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие среднего арифметического

Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Вот так:

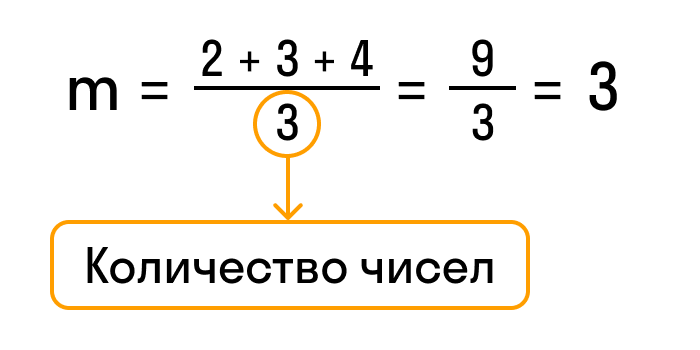
Например, найдем среднее арифметическое чисел 5, 6 и 7. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.

Разделим результат на количество чисел в задании, то есть на три.

Так получилась формула среднего арифметического:

Способы вычисления среднего арифметического

Стандартная формула. Чтобы найти среднее арифметическое, нужно сложить все числа и поделить эту сумму на их количество. Формула выглядит так:

Вычисление моды или наиболее часто встречающегося значения. Формула такая:

Вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. Если такого значения нет, за медиану принимают среднее число между границами половин выборки. Формула выглядит так:

Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: в магазине, на работе, в диалоге с другом или во время презентации перед инвесторами. Еще пригодятся, чтобы рассчитать среднюю скорость движения.

Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:

Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.

Примеры расчета среднего арифметического

Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.

Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.

Пример 2. Посчитать среднее арифметическое 7,5 и 8 и 0,5.

Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.

Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.

Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.

Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.

Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.

Ответ: школьник в неделю тратит в среднем 81 рубль.

В 5 классе можно искать среднее арифметическое с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

Источник

Как правильно вычислить среднее значение?

Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.

В чем проблема?

Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.

Давайте обратимся к классическому примеру со средней зарплатой.

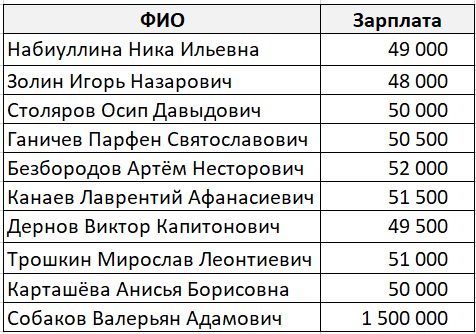
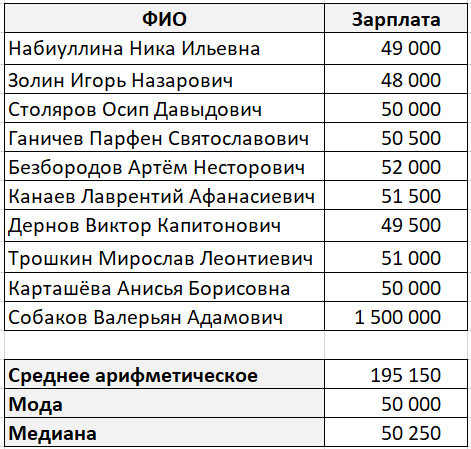
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).

Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.

Какие способы вычисления среднего бывают?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.

Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.

Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).

А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:

И вот какие значения у нас получились:

В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.

Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.

Вычисляем среднее арифметическое на SQL

И чтобы ее использовать достаточно написать вот такой запрос:

Вычисляем моду на SQL

В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.

Вычисляем медиану на SQL

Выглядит все это так:

Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.

Какой способ все-таки использовать?

Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.

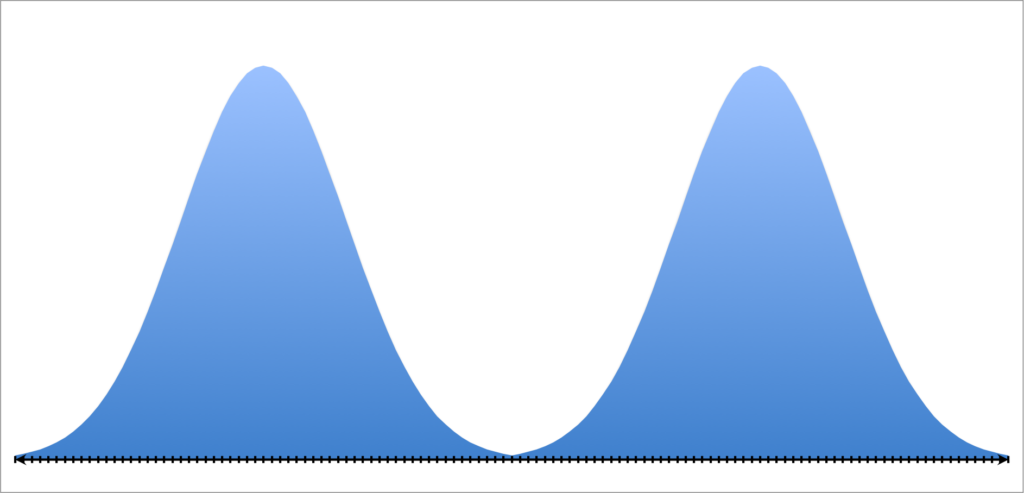
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:

На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.

В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.

А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.

Вывод:

При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.

Окончательный выбор меры центральной тенденции всегда лежит на аналитике.

Источник

Среднее арифметическое: физический смысл и визуализация

Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:

Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.

Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.

Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.

Среднее арифметическое двух чисел

Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:

Их среднее арифметическое:

Физический смысл среднего арифметического

Изобразим два исходных числа и их среднее арифметическое на числовой оси:

Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.

В механике момент силы – это произведение силы F на расстояние l:

На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l₁ и l₂, получим:

Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:

Обозначив m координату точки опоры весов, получим:

Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:

Координата опоры весов m:

Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.

Визуальное восприятие равновесия

Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.

Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:

На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.

Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:

Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.

Математическое ожидание случайной величины

Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:

Теперь точка опоры весов в равновесии это μ:

Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:

Это и есть формула математического ожидания.

Гистограмма

Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.

На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.

Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:

Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:

Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:

Дайте мне точку опоры, и я переверну Землю. Архимед

Источник

Среднее арифметическое

Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами.

Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).

При стремлении количества элементов множества чисел стационарного случайного процесса к бесконечности среднее арифметическое стремится к математическому ожиданию случайной величины.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.

Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным.

В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями.

Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее степенное, взвешенные средние, центр сгиба, медиана, мода.

Источник

Среднее арифметическое

Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами [1] и является одной из наиболее распространенных мер центральной тенденции.

Частными случаями среднего арифметического являются генеральное среднее ( генеральной совокупности) и выборочное среднее ( выборки).

Содержание

Введение

Обозначим множество данных X = (x₁, x₂, …, x_n), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (, произносится «x с чертой»).

Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки x_i из этой совокупности μ = E<x_i> есть математическое ожидание этой выборки.

На практике разница между μ и в том, что μ является типичной ненаблюдаемой переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).

Обе эти величины вычисляются одним и тем же способом:

Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.

В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.

Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.

Примеры

Непрерывная случайная величина

Для непрерывно распределённой величины среднее арифметическое на отрезке определяется через определённый интеграл:

Некоторые проблемы применения среднего

Отсутствие робастности

Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.

Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.

Сложный процент

Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.

Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только 8,2 %.

В общем, сложный процент даёт 90 % * 130 % = 117 % общий рост, а годовой прирост , то есть 8,2 % в год.

Направления

Особую осторожность нужно иметь при расчёте циклических данных, таких как фазы или углы. Наивное вычисление среднего арифметического 1° и 359° даёт результат 180°. Это неверно по двум причинам:

В целом применение такого рассмотрения средней величины ведёт к искусственному сдвигу его к середине числового диапазона. Решение этой проблемы заключается в использовании оптимальной формализации (а именно, определение среднего в качестве центральной точки, то есть точки, от которой наименьшая дисперсия), а также переопределение вычитания как модульного расстояния (то есть как расстояние от окружности; в частности, модульное расстояние между 1° и 359° — это 2°, а не 358°).

Источник