Что означает сочетательное свойство
Свойства умножения и деления
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется.
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
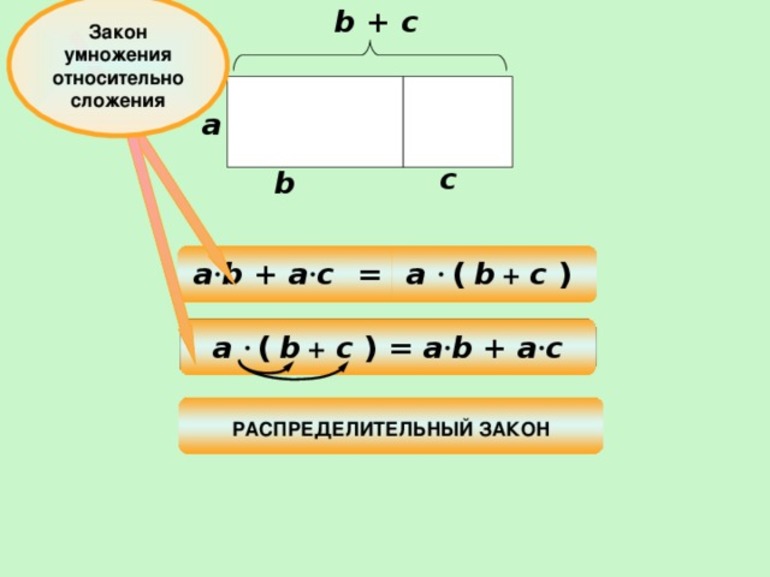
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
В обратную сторону распределительное свойство умножения относительно сложения звучит так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
В обратную сторону распределительное свойство умножения относительно вычитания звучит так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число.
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?
Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.
Пример 2
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 3
Упростить выражение: 27a – 16a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.
Общие сведения
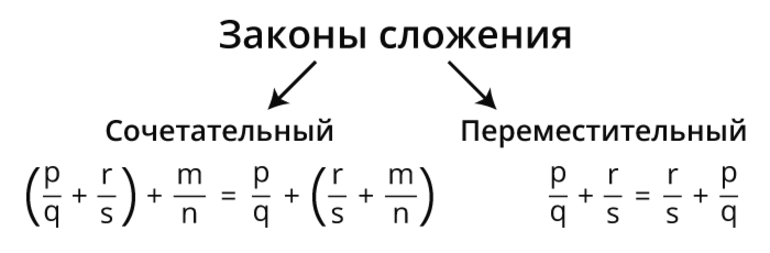
Сложение является одной из базовых арифметических операций в математике. Оно изучается во втором классе общеобразовательной школы. Существует всего 2 правила: переместительный и сочетательный закон сложения. Однако многие ученики часто их путают. Разобраться в этом помогут специалисты. Они разработали специальную методику, позволяющую быстро запомнить различие между ними.
Однако для изучения алгоритма нужно знать базовые термины и определения. К ним относятся:
Сложение состоит минимум из трех элементов: двух слагаемых (одно из них увеличивается на другое) и результата. Последний называется суммой. На примере это выглядит так: 5+9=14, где 5 — I слагаемое, 9 — второй элемент-слагаемое или число, на которое нужно увеличить первое слагаемое, а 14 — их сумма.
Переместительное правило
Переместительное (коммутативное) правило является очень простым для понимания. Оно формулируется следующим образом: если поменять местами слагаемые, их сумма не изменится. Математическая форма записи закона выглядит следующим образом: q+w=s.
На практическом примере правило реализуется в таком виде: 5+6=6+5=11. Последнее числовое выражение очень легко проверить. Для этого достаточно воспользоваться обыкновенным калькулятором. При сложении 5 и 6 он покажет величину, равную 11. Следует отметить, что таким образом и доказывается закон переместительного свойства сложения.
Прием практической реализации для доказательства правил и утверждений применяется очень часто. Это и есть оптимальная методика, позволяющая выяснить работоспособность того или иного утверждения. Далее необходимо рассмотреть сочетательный закон сложения.
Сочетательный закон
Сочетательное правило сложения возможно применить, когда числовое выражение включает в свой состав от трех и более слагаемых. Сочетательный закон сложения во 2 классе можно сформулировать следующим образом: слагаемые, входящие в состав выражения, можно для удобства складывать в любом порядке.
Очень часто правило называют ассоциативным свойством операции сложения. Ее математическая запись имеет такой вид: p+r+s=(p+s)+r=(s+r)+p=z. Чтобы доказать утверждение, нужно решить пример «2+9+8+1». Его специалисты рекомендуют решать по такому алгоритму:
К сочетательному свойству также можно применить и переместительное (коммуникативное) правило. Этим приемом очень часто пользуются специалисты. Кроме того, по-другому ассоциативный закон называется методом группировки чисел. Далее нужно рассмотреть методику применения двух законов на практике.
Методика применения
Методика использования правил сложения зависит от конкретного примера. Однако специалисты рекомендуют придерживаться следующего алгоритма нахождения результатов числовых выражений:
Сочетание элементов можно выполнять несколько раз, т. е. вычислить сначала одно значение, а потом опять перегруппировать выражение. Перемену мест слагаемых можно производить в несколько заходов.
Кроме того, законы сложения можно применять не только для целых чисел, но и для дробных. Для совершенствования качества усвоения теоретического материала рекомендуется придумать примеры и решить их.
Некоторые ученики часто путают принадлежность распределительного правила к суммации двух и более величин. Этого делать не нужно, а требуется запомнить, что у сложения только 2 закона, но не 3. Последний принадлежит только операциям деления и умножения.
Переместительное и сочетательное свойства можно применять и для вычитания. Далее необходимо на практическом примере разобрать использование правил сложения и методику их применения.
Пример решения
Для закрепления теоретического материала необходимо решить следующий пример: 4+9+6+5+1+15+17+2+12+1. Находится решение по такому алгоритму:
Следует учитывать, что группировку элементов можно выполнять в произвольном порядке и количестве. Суть метода — достижение максимальной скорости вычислений при сложении простых элементов, позволяющих без проблем произвести расчеты.
Если сразу выполнить расчеты сложно, рекомендуется группировать числа по количеству знаков, т. е. однозначные с однозначными, двузначные с двузначными и т. д.
Таким образом, сочетательный и переместительный законы применяются в математике для ускорения вычислений.
Общие сведения
В математике любое действие принято называть операцией. Согласно математическому определению под ней понимают представления соответствия одному или нескольких элементам аргумента иного элемента. Все операции разделяют на арифметические и гипероперации. К первым относят сложение и вычитание. Вторые же включают в себя:
При умножении участвуют два члена (аргумента). Один из них называют множителем, а другой сомножителем. Но вместе с тем в учебниках используют и другие названия — множимое и множитель. Результатом умножения является не что иное, как произведение. Так как перемножение по своей сути является коммутативной операцией, то есть характеризуется свойством переместительности, порядок записи членов не оказывает влияния на результат.
Наряду с таблицей существуют и законы умножения. В 5 классе среднеобразовательной школы учащиеся проходят эти свойства, закладывая фундамент для освоения быстрого счёта. По своей сути произведение является результатом сложения одного из чисел столько раз, сколько указывает второе. Например, пусть имеется девять рядов. В каждом из них лежит пятнадцать яблок. Чтобы вычислить, сколько же всего фруктов необходимо, нужно сложить число пятнадцать само с собой девять раз. В ответе и получится искомое количество.
Эта неудобная операция сложения заменяется умножением. Другими словами, нужно просто число рядов умножить на количество яблок в каждом из них: k = 15 * 9 = 135 штук. При этом, согласно свойству умножения, порядок перемножения не имеет значения, так k = 9 * 15 = 135 штук.
Под умножением двух натуральных чисел понимают действие, результат которого равен сумме одинаковых слагаемых, определяемой первым из умножаемых чисел. При этом второе из этих чисел указывает количество слагаемых. В этом и заключена суть умножения двух натуральных чисел. Можно сформулировать простое определение действию: под произведением понимают результат, полученный суммированием слагаемого, при этом одно из перемножаемых чисел указывает на количество слагаемых.
Свойства произведения
Изучение математиками процесса умножения позволило им обнаружить ряд закономерностей, характерных для этого действия. Их назвали свойствами умножения. Наиболее часто при решении задач, при котором используется нахождение произведения, используют шесть законов умножения:
Сочетательный и переместительный законы были получены путём изучения результатов действия сложения. Они довольно похожи между собой. При сложении используется два правила: от перемены мест слагаемых результат остаётся неизменным, и при сложении нескольких членов можно сложить только два из них, а после полученную сумму прибавить к оставшимся. Именно на этих свойствах и построены два закона умножения. Сочетательное свойство сложения и умножения вместе с переместительным законом используют для существенного ускорения расчётов.
Например, пусть необходимо вычислить выражение: 15 * 3 * 4 * 5 + 1 * 2 * 3 * 4 * 5 * 6. Пример состоит из двух слагаемых. Первое, используя сочетательный закон, можно упростить. То есть не выполнять перемножение последовательно, что трудно сделать в уме, а вначале умножить первый и второй член, а затем третий с четвёртым, а уже после полученные произведения перемножить между собой: (15 * 3) * (4 * 5) = 45 * 20 = 900. Второе же слагаемое проще вычислить последовательно. В итоге получится: 900 + 720 = 1620.
Формулировка и объяснение
Сочетательный закон, а его часто называют ассоциативным, гласит, что при умножении любого количества множителей результат не поменяется, если группу этих множителей подменить произведением. Математической формулой это утверждение можно записать в виде: a * b * c = (a * b) * c = a * (b * c).
Для понимания этого действия нужно представить прямоугольник со сторонами три и пять сантиметров, нарисованный на тетрадном листе в клетку. Фигуру можно разбить на одинаковые единичные (сантиметровые) квадраты, а после подсчитать их количество. Сделать это можно несколькими способами.
Например, зная, что общее количество квадратов будет равняться произведению пяти на три, а каждый квадрат образуется четырьмя клетками, общее число будет равняться n = (5 * 3) *4 = 60 штук. Другой способ можно построить на том, что в каждом столбце находится три квадрата. Отсюда следует, что столбец содержит 3 * 4 клетки. Общее число клеток будет равняться: 5 * (3 * 4) = 60 штук.
Получается, что два способа равноправны, то есть (5 * 3) * 4 = 5 * (3 * 4). Таким образом, если заменить члены буквенным обозначением, то получится сочетательное свойство умножения. Отсюда следует ещё одно правило. Оно позволяет не только менять местами множители, но и вносить их под знак скобки, тем самым определяя порядок решения.
Распределительное свойство удобно применять и относительно сложения и вычитания. Пусть имеется отрезок разделяющий прямоугольник. Количество единичных квадратов, с одной стороны, будет равняться произведению трёх умноженному на три, а с другой — трёх на два. В итоге получится: 3 * 3 + 3 * 2 = 15 штук. Иначе можно утверждать, что в каждой строчке фигуры размещены 3 + 2 квадрата. Исходя из этого, верно будет записать: 3 * (3 + 2) = 15 штук. Равенство 3 * 3 + 3 * 2 = 3 * (3+ 2) и есть распределительное свойство, довольно плотно использующееся с сочетательным законом.
Например, нужно найти результат действия 25 *1349 * 4. Используя переместительное и сочетательное свойство, удобно выполнить перестановку членов, благодаря чему можно найти ответ. Так, удобно объединить члены выражения следующим образом: 25 * 1349 * 4 = 1349* (25 * 4) = 1349 * 100 = 134900. Аналогичным образом можно поступить и при присутствии в задании знака сложения или вычитания. Например, 311 * 734 + 329 * 266 = 311 * (734 + 266) = 311 * 1000 = 311 000.
Решение примеров
Необходимо не только понять сочетательный закон, но и уметь применять его в практических заданиях. Тем более что решение примеров позволит закрепить теоретический материал и довести действия до автоматизма. Получив опыт группирования членов, можно будет, затрачивая минимальные усилия, перемножить любой сложности выражения. При этом некоторые действия даже выполнить в уме.
Существует несколько условий применения сочетательного свойства: в задании не может быть менее трёх числовых значений; выражение должно содержать только все знаки сложения или умножения. Например, для следующих выражений: 6 * 55 — 3, 6 * 34, 4 * 9 *12, 34:5 * 8, 4 *9 *234, закон применим только ко второму и последнему.
Вот ряд примеров, предназначенных для самостоятельного решения:
Следует отметить, что для освоения сочетательного свойства обычно хватает самостоятельно решить около двадцати различных примеров. При этом для проверки результата можно использовать обычный калькулятор или даже онлайн-калькуляторы.
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 16. Свойства сложения. Применение переместительного и сочетательного свойств сложения
Перечень вопросов, рассматриваемых в теме:
— Что такое сочетательное свойство сложения?
-В каких случаях можно использовать свойства сложения?
Переместительное свойство сложения: слагаемые можно переставлять местами, при этом значение суммы не изменится.
Сочетательное свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.44-47
2. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций/ Глаголева Ю.И., Волкова А.Д.-М.: Просвещение, Учлит, 2017, с.18, 19
3. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.- с.28, 29
Теоретический материал для самостоятельного изучения
Сравним выражения и их значения:
Сумма чисел шесть и девять равна сумме чисел девять и шесть.
Сумма чисел сорок пять и пять равна сумме чисел пять и сорок пять.
Значения выражений равны, так как от перестановки слагаемых значение суммы не меняется. Вспомним, как в математике называется данное свойство сложения?
Правильно, оно называется переместительным свойством сложения.
В школьном спортзале 3 волейбольных мяча, 5 баскетбольных мячей и 4 футбольных мяча. Сколько всего мячей в спортзале?
Первый способ решения.
Сначала узнаем, сколько волейбольных и баскетбольных мячей, затем прибавим число футбольных мячей. Запишем: к сумме чисел три и пять прибавить четыре, получится двенадцать.
Второй способ решения.
Прибавим к числу волейбольных мячей сумму баскетбольных и футбольных мячей. Запишем: к трем прибавить сумму чисел пять и четыре равно двенадцать.
В обоих случаях получили одинаковый результат, значит, выражения равны между собой. Можем записать так: (3+5)+4=3+(5+4)
Теперь ты знаешь еще одно свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой. Это свойство называется сочетательным свойством сложения.
Знание этих двух свойств сложения позволит нам решать примеры на сложение удобным способом.
Решим выражение: 1+7+9+3=?
Мы знаем, что слагаемые можно менять местами и соседние слагаемые заменять их суммой. Воспользуемся свойствами сложения и найдем сумму.
В данном случае удобно сложить попарно 1 и 9, 7 и 3. А затем сложить полученные результаты. Получим 20.
Делаем вывод: используя переместительное и сочетательное свойства сложения можно складывать числа в любом порядке, как удобнее.
1. Вычислите суммы удобным способом
30 + 3 + 7 + 40 = _________ 4 + 10 + 6 + 70=_______________
1. 30 + 3 + 7 + 40 = (3+7)+(30+40)=80 2. 4 + 10 + 6 + 70= (10+70)+(4+6)
2. Совместите название математического свойства с его значением и выражением
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
Свойства сложения и вычитания
Свойства (или законы) арифметических действий на числовых примерах мы рассматривали в теме «Законы арифметики» для начальной школы.
В 5 классе законы арифметики записываются с помощью буквенных выражений. Поэтому теперь мы рассмотрим эти и другие свойства в виде буквенных выражений.
Свойства сложения
Переместительное свойство сложения
От перестановки слагаемых сумма не меняется.
В буквенном виде свойство записывается так:
Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.
Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто « a + b + с ».
Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.
При сложении нескольких чисел их можно как угодно объединять в группы и переставлять.
Свойство нуля при сложении
Сумма двух натуральных чисел всегда больше каждого из слагаемых. Но это не так, если хотя бы одно из слагаемых равно нулю.
Если к числу прибавить нуль, получится само число.
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.
Скобки в выражении « (a − b) − c » не имеют значения и их можно опустить.
Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
Если из числа вычесть само число, то получится нуль.