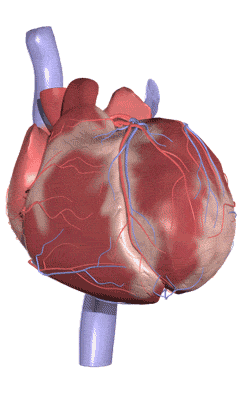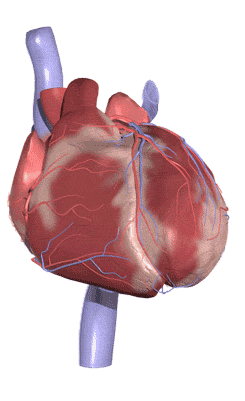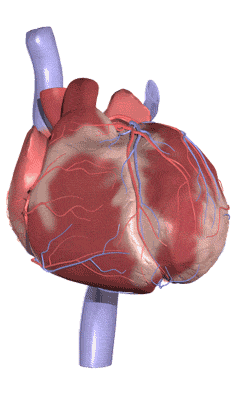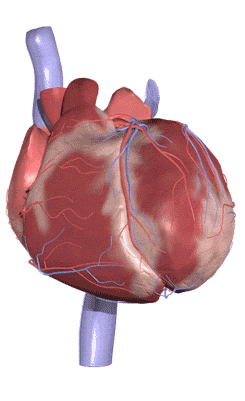
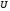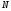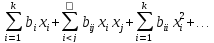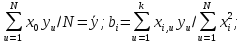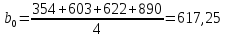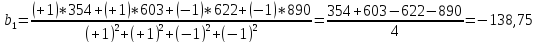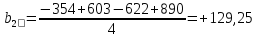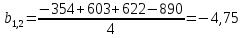Что означает слово моделирование в биологии
Модели (в биологии)
В биологии применяются в основном три вида М.: биологические, физико-химические и математические (логико-математические). Биологические М. воспроизводят на лабораторных животных определённые состояния или заболевания, встречающиеся у человека или животных. Это позволяет изучать в эксперименте механизмы возникновения данного состояния или заболевания, его течение и исход, воздействовать на его протекание. Примеры таких М. — искусственно вызванные генетические нарушения, инфекционные процессы, интоксикации, воспроизведение гипертонического и гипоксического состоянии, злокачественных новообразований, гиперфункции или гипофункции некоторых органов, а также неврозов и эмоциональных состояний. Для создания биологической М. применяют различные способы воздействия на генетический аппарат, заражение микробами, введение токсинов, удаление отдельных органов или введение продуктов их жизнедеятельности (например, гормонов), различные воздействия на центральную и периферическую нервную систему, исключение из пищи тех или иных веществ, помещение в искусственно создаваемую среду обитания и многие другие способы. Биологические М. широко используются в генетике, физиологии, фармакологии.
Значительно большие успехи достигнуты в моделировании физико-химических условий существования живых организмов или их органов и клеток. Так, подобраны растворы неорганических и органических веществ (растворы Рингера, Локка, Тироде и др.), имитирующие внутреннюю среду организма и поддерживающие существование изолированных органов или культивируемых вне организма клеток (см. Культуры тканей ).
М. биологических мембран (плёнка из природных фосфолипидов разделяет раствор электролита) позволяют исследовать физико-химические основы процессов транспорта ионов и влияние на него различных факторов. С помощью химических реакций, протекающих в растворах в автоколебательном режиме, моделируют колебательные процессы, характерные для многих биологических феноменов, — дифференцировки, морфогенеза, явлений в сложных нейронных сетях и т. д.
Лит.: Моделирование в биологии. Сб. ст., пер. с англ., М., 1963; Новик И. Б., О моделировании сложных систем, М., 1965; Кулагина О. С., Ляпунов А. А., К вопросу о моделировании эволюционного процесса, в кн.: Проблемы кибернетики, в. 16, М., 1966; Модели структурно-функциональной организации некоторых биологических систем. [Сб. ст.], М., 1966; Математическое моделирование жизненных процессов. Сб. ст., М., 1968; Теоретическая и математическая биология, пер. с англ., М., 1968; Моделирование в биологии и медицине, Л., 1969; Бейли Н., Математика в биологии и медицине, пер. с англ., М., 1970; Управление и информационные процессы в живой природе, М., 1971; Эйген М., Молекулярная самоорганизация и ранние стадии эволюции, «Успехи физических наук», 1973, т. 109, в. 3.
wiki.vspu.ru
портал образовательных ресурсов
«Задачи Биологии решаемые с помощью компьютерного моделирования»
Выполнила Гарькуша Анастасия 10 Б
В биологии применяются в основном три вида моделей: биологические, физико-химические и математические (логико-математические).
В реальном времени нужный для науки оригинал может уже не существовать или же существовать, но в разных частях света ( например вымирание Динозавров ) и чтобы собрать общую картину похожую на оригинал нам будет необходимо компьютерное моделирование.
С помощью компьютерного моделирования мы можем создавать наглядные примеры внутренних органов и всего организма в целом.
Чтобы рассмотреть модель клетки мы можем использовать компьютерное моделирование и узнать строение досконально.
При помощи компьютерного моделирования мы можем создать модель всех внутренних органов и исследовать их не нанося ущерб здоровью организма.
Вывод : Компьютерное моделирование очень важно для будущего науки в Биологии, так как с помощью него мы можем исследовать все аспекты жизнедеятельности организма, изучать строение живых существ даже если их уже не существует.
Моделирование в биологии
Современное развитие биотехнологии невозможно без широкого применения методов математического планирования экспериментов. Начало математическому планированию экспериментов положили в 30-х годах работы Р. Фишера. В частности, им были разработаны планы полного факторного эксперимента. Данные методы в первую очередь нашли широкое применение при решении задач оптимизации химико-технологических процессов и только в последнее время начали использоваться в биологии.
Просмотр содержимого документа
«Моделирование в биологии»
Моделирование в биологии
Одним из основных направлений работы с мотивированными детьми в первую очередь является выполнение учебно-исследовательских проектов. Учебно-исследовательская деятельность учащихся направлена на выполнение следующих задач:
— подготовка образованных, развитых, способных самостоятельно решать практические задачи выпускников школ;
— приобретение учащимися необходимых знаний сверх учебного плана путем самостоятельных научных поисков и анализа;
— обучение методике и средством самостоятельного решения научных и практических задач;
— воспитание учащихся в духе требований сегодняшнего дня: патриотизма, творческого энтузиазма, научный принципиальность и деловой этики;
— приобретение школьниками организаторских навыков, навыков общения и педагогического мастерства;
— привитие навыков постоянный самостоятельной работе, т.е. самообразованию.
Учебно-исследовательская работа учащихся связана как с учебным процессом, так и с внеурочной деятельностью, которая заключается в участии учеников в кружках, в научном обществе, факультативах и т.д. К учебно-исследовательской работе во внеурочное время привлекаются школьники всех ступеней обучения, имеющие желания и склонность к исследованиям.
Важным этапом проектно-исследовательской деятельности школьников является подведение итогов работы, которые предоставляются в виде докладов, рефератов, исследовательских проектов и их защиты на школьных, окружных, областных конференциях и конкурса. Основным требованием, предъявляемым к оформлению исследовательской работы учащихся, является выбор методов исследования, соответствующих заявленной теме исследования и объектом и предметом изучения
Основная часть работы должно отражать следующие этапы:
а) выбора направления исследований;
б) теоретические и экспериментальные исследования;
в) обобщения или оценку результатов исследования
В пособии представлены материалы, охватывающие, как теоретический материал для учителей, так и практические задания для учащихся эколого-биологического содержания, основанные на методе моделирования.
2. Моделирование в биологии
Разработка полезна всем, кто применяет математические методы постановки и обработки эксперимента. Описывается алгоритм составления математической модели при проведении эксперимента
2.1 Методы моделирования активного эксперимента
Современное развитие биотехнологии невозможно без широкого применения методов математического планирования экспериментов. Начало математическому планированию экспериментов положили в 30-х годах работы Р. Фишера. В частности, им были разработаны планы полного факторного эксперимента. Данные методы в первую очередь нашли широкое применение при решении задач оптимизации химико-технологических процессов и только в последнее время начали использоваться в биологии.
Основным преимуществом математического планирования, по сравнению с классическими методами исследования, является возможность одновременного влияния на эффективность процесса большого числа факторов. Кроме того, этот метод позволяет наряду с количественным учетом каждого отдельного фактора установить наличие в системе межфакторных взаимодействий и оценить эффект последних, а также определить значения параметров при оптимальной эффективности процессов.
Постановка задачи оптимизации
В ходе многих биоэкологических процессов( в нашем примере при производстве хлеба в хлебопечении) часто возникает задача выбора оптимальных условий процесса, протекание которого зависит от большого числа факторов. Оптимальность протекания процесса при выбранном соотношении условий (факторов внешней среды) оценивается параметрами, или категориями, оптимизации. Важным вопросом экспериментального исследования является выбор критерия оптимизации. Критерии оптимизации включают в себя экономические показатели и должны иметь численное выражение. Если ставится задача оптимизировать какую-либо часть технологического процесса, то за частный критерий оптимизации принимают технологический параметр. В биотехнологических процессах такими частными критериями оптимизации могут быть: выход биомассы продукта, себестоимость продукта и т. д. Задачей исследования является нахождение путем проведения некоторого количества экспериментов при различных сочетаниях уровней факторов максимальной и минимальной величин выбранного критерия (параметра) оптимизации.
Способы решения задачи оптимизации. Метод Бокса
Наиболее широкое применение для решения описанных выше задач оптимизации получил в последнее время метод Бокса. По этому методу вблизи исходной точки («фона») ставится специальным образом спланированная небольшая серия опытов, в которой одновременно варьируются все изучаемые факторы, каждый – на двух уровнях (верхнем и нижнем). Результаты данных опытов математически обрабатываются для получения линейного приближенного уравнения, по которому можно найти направление количественного изменения факторов для наиболее короткого движения к оптимуму (метод крутого восхождения).
Затем ставят большую по объему серию опытов для более точного математического описания указанной области. По этому математическому описанию рассчитывают оптимальные условия ведения процесса. Прежде чем приступить к ее подробному разбору, остановимся на требованиях, предъявляемых к факторам:
– факторы должны быть управляемыми, т. е. установлены на выбранных уровнях;
– факторы должны быть однозначными и непосредственно воздействовать на объект;
– точность измерения факторов должна отвечать поставленной задаче;
– факторы должны быть совместимыми; это означает, что все их комбинации осуществимы и безопасны;
– факторы должны быть независимыми, т. е. каждый из факторов может быть установлен на любом уровне независимо от уровней других факторов.
Производство хлеба – более сложный процесс. Он включает в себя следующие основные стадии: солодоращение, приготовление пивного сусла, охмеление сусла, сбраживание пивного сусла дрож- жами, дображивание и созревание пива. Каждая из перечисленных стадий характеризуется своими критериями оптимизации, на которые влияют различные биохимические и физико-химические факторы.
Моделирование активного эксперимента
На исследуемое явление, точнее на его параметры y1, y2,y3 и т.д. влияют многие переменные факторы: x1, x2, x3и т.д. Изучение влияния этих факторов возможно как путем простого наблюдения (пассивный эксперимент), так и путем воздействия на объект исследования с целью создания различного сочетания влияющих факторов (активный эксперимент) Активный эксперимент с целью исследования механизма процесса (построения его модели) и с целью его оптимизации планируется двумя способами:
– как однофакторный, в этом случае традиционный план заключается в измерении какого-либо оптимизируемого параметра y при различных значениях одного из факторов (например, x1, при поддержании всех остальных факторов на строго постоянном уровне);
– как многофакторный, т.е. с варьированием от опыта к опыту сразу всех влияющих факторов (или с поддержанием на постоянном уровне лишь некоторых из них). Математическое планирование многофакторного эксперимента основано на выборе оптимального количества опытов. Количество опытов при этом
где m– количество уровней для факторов, k– количество факторов.
Рассмотрим последовательность операций в ПФЭ:
Табл. 1.1 Таблица кодирования
Факторы (наименования, размерности, обозначения)
2. Составление матрицы планирования, т.е. перечня из N опытов со всеми возможными сочетаниями уровней всех исследуемых факторов.
Табл. 1.2 Матрица кодирования
4. По полученным экспериментальным результатам расчет коэффициентов уравнения регрессии, которое в наиболее общем виде выглядит так:
y = b0 +
Без учета квадратичных эффектов для ПФЭ типа 2 2 уравнение имеет вид:
а при полном отсутствии взаимодействия (корреляций) справедлива линейная модель:
Формулы для расчета коэффициентов по методу наименьших квадратов:
b0 =
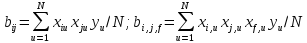
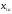

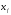
5. Анализ полученных уравнений с целью принятия решений, например, для определения оптимальных условий процесса. Для этого производится пересчет кодированных значений факторов xiв натуральныеXi и обратно по формуле:
где: xi– кодированное значение фактора (в долях интервала кодированияXi), Xiи 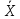
Δ 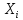
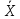
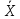
Исследовано влияние времени обработки воды в электролизере под влиянием постоянного тока и концентрации активированной воды на подъемную силу хлебопекарных дрожжей.
Рассчитать количество необходимых для ПФЭ опытов, составить таблицу кодирования факторов и матрицу планирования эксперимента. Составить уравнение регрессии и определить значимость коэффициентов в уравнении.
В качестве исследуемых были выбраны следующие факторы: время обработки воды X1, с, степень разбавления воды X2,%. ( в качестве входных переменных X), За критерий качества полученной продукции принята подъемная сила дрожжей y (как выходная величина). Эксперимент был спланирован как двухфакторный. Для двухуровневого полного факторного эксперимента ПФЭ количество опытов: N = 2k =4 опыта. Ниже перечисляется последовательность операций в эксперименте.
Последовательность операций математического планирования эксперимента
А. Кодирование факторов и составление матрицы планирования эксперимента
Факторы и размерности
Кодированные значения, x
Натуральное значение фактора.
Натуральное значение фактора Разбавление воды, (X2), %
Таб.2. Матрица планирования

Б. Проведение серии экспериментов по определению влияния активности воды на подъемную силу дрожжей в тесте на основе этой воды согласно плану (который предусматривает реализацию N = 4 опытов), представленному матрицей планирования.
Таб. 3. Условия и результаты эксперимента. Влияние активной воды на свойства дрожжей
Время обработки воды, мин
Подъемная сила дрожжей, с
В. Расчет коэффициентов в уравнении регрессии линейного вида с учетом взаимодействия факторов. Составление уравнения регрессии y по x1 и x2.
Расчет ведем по уравнению: y = b0 + b1x1 + b2x2 +b1,2x1x2
Обработка экспериментальных данных по известной методике позволила получить оценки коэффициентов двухфакторного уравнения регрессии
Реализация эксперимента и обработка его результатов позволила получить математическую модель линейного вида, описывающую зависимость подъемной силы дрожжей y от времени активации воды и степени разбавления активной воды, которая имеет вид:
Из полученного уравнения видно, что в исследованном интервале времени обработки воды и степени разбавления активной воды подъемная сила дрожжей возрастает с увеличением времени обработки воды и уменьшается с увеличением разбавления обработанной воды.
Г. Оценка значимости коэффициентов уравнения регрессии. Расчёт погрешности и критерия Стьюдента по результатам параллельных опытов.
Точность и ошибку эксперимента определяли по центральной точке планирования. Были проведены 6 параллельных опытов при среднем значении времени обработки воды (6,5 минут), Проверку значимости коэффициентов уравнения регрессии проводили по статистическому критерию Стьюдента. Результаты этих расчетов сведены в ПРИЛОЖЕНИИ 2, таб.П 6.
Таб. 4 Расчет дисперсии воспроизводимости
Средняя арифметическая подъемной силы дрожжей, с
Дисперсия, 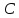
Среднее квадратичное отклонение (сигма) определяли по формуле
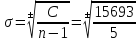
После вычисления сигмы для всех коэффициентов уравнения регрессии составляется ti–отношение:ti = bi/ σ,
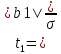
Проверяется условие ti≥ tст где tст– табличное значение критерия Стьюдента, v – число степеней свободы, равное n-1, то есть равное 5. Если условие выполняется, то коэффициент считают статистически значимым. Если условие не выполняется, то коэффициент считают незначимым, то есть равным нулю. Стандартное значение критерия Стьюдента при уровне значимости =0,10 и числе степеней свободы v =5 равно 2,015.
Проверяется условие для коэффициента b1:t1≥tст;2,478 ≥2,015.
Проверяется условие для коэффициентаb2:t2≥tст;2,313 ≥2,015.
Таб.5 Результаты оптимизации
Среднее квадратичное отклонение,
Расчетное значение критерия Стьюдента
Табличное значение критерия Стьюдента
Сравнение расчетной величины t1 и t2 с табличным значением критерия Стьюдента tст=2,015 (при числе степеней свободы =5 и принятой доверительной вероятности Р=90%) показывает выполнение условия ti≥ tст. Результаты таблицы 5 указывают на достоверность и надежность коэффициентов в уравнении регрессии. Модель процесса производства хлеба для исследованной области изменения факторов имеет вид:
где x1–кодированное время обработки воды (с); x2–кодированная степень разбавления воды (%); y –подъемная сила дрожжей, с
Д. Обсуждение результатов исследования
Для увеличения активности воды целесообразно проводить обработку в максимально возможном режиме и не разбавлять жидкость;
2.2 Моделирование –метод эколого-биологических исследований
2.. Графические – схема, план, рисунок экосистемы.
3.Математические – графики, диаграммы, уравнения для описания измерения факторов в экосистемах.
5. Химические – модели, демонстрирующие химические процессы, протекающие в биосфере.
Как модели помогают решать проблемы?
Рассмотрим такой пример. Вода в Средиземном море чуть более соленая чем по соседству, в Атлантическом океане (на 5% с небольшим). Почему? Исследования Геологов показывают, что в донных и береговых осадков здесь имеются большие толщины отложенной соли, образовавшийся примерно 7 миллионов лет назад. Но как за такое короткое по геологическим масштабом время тут могли сложиться подобные запаса?
Практическая работа №1. Моделирование экологического состояния водоема
Составьте схему экосистемы водоема, в котором вы проводили наблюдения за состоянием воды;
Составьте описание источников антропогенных загрязнений в экосистеме;
Постройте графики и диаграммы для описания изменения абиотических и биотических факторов;
Постройте из картона, бумаги, пластилина, дерева или других материалов в техническую модель-макет одного из участков экосистема.
Укажите параметры, по изменениям которых можно достаточно точно судить об изменении качества питьевой воды.
Как изменится качество питьевой воды в стакане, если его продержать у открытого окна под прямыми солнечными лучами в течении дня?
Было установлено, что в водоеме имеются болезнетворные микробы. Однако дополнительное взятия нескольких проб не подтвердило их присутствие. Предложите объяснение этим факторам.
Каждую весну водопроводная вода в одном из городов приобретает светло-желтый цвет. Какие измерения необходимо провести для установления причины изменения цвета воды?
2.3. Математические модели биологических объектов, явлений и процессов
1. Модель однородной популяции
Численность (плотность) популяции в момент t равна x(t). Относительный прирост популяции через промежуток времени
Закон изменения численности популяции представляется следующим дифференциальным уравнением:
xi+1 = xi+axi-bxi2; x0 = c, i = 0.1. n,
где n предельное время моделирования.
Рассчитайте, как меняется численность популяции со временем, если а=1, b=0,0001 при начальной численности, равной 10. Какова численность популяции через очень большой промежуток времени (стабильная популяция).
Имеются популяции двух видов, которые представляются отношениями
Определить характер зависимости периодических коле-баний численности жертв (хищников) от ai, bi, ci, gi и динамику зависимости y=f(x).
В изолированном поселке с населением m человек возникла эпидемия болезни, распространение которой описывается соотношениями:
Более строго соотношение может быть получено из системы дифференциальных уравнений:
Построить графики изменений
Построить графики изменений
Для определения прогноза урожая можно воспользоваться экспериментальной зависимостью
Вычислить прогноз урожайности сельхозкультуры по различным значениям факторов xi.
Раковая опухоль обычно увеличивается экспоненциально в соответствии с дифференциальным уравнением:
Определить, при каких значениях параметров С существует предельный размер опухоли. Выяснить, при каких значениях С рост опухоли не превосходит некоторой конечной величины.
6 Модель растворения лекарственного препарата
Рассчитать кинетику расходования лекарственного препарата при следующих параметрах: а = 2/3, k1= 0-1, Lmax = 0.1-0.8, n = 1, ka = 0.1.
Как будет изменяться кинетический процесс при изменении параметров путем увеличения и уменьшения на шаг h. Как зависит процесс расходования лекарственных препаратов от температуры.
Экологические последствия вырубки тропических лесов поистине трагичны. Вполне вероятно, что в настоящее время мы полностью не можем оценить размеров этой катастрофы. Что же касается воздействие вырубки на изменения глобального климата и его элементов, то они мало ощутимы.
Последние десятилетия в пресноводных бассейнов в скандинавских стран наблюдаются весьма крупные заморы рыбы; они происходят сразу после зимней оттепели и с наступлением весны. Исследователи связывают замор с очень резким повышением именно в эти периоды кислотности воды, однако причина заморов до конца осталось невыясненной.
Сейчас специалисты проводят сравнительное изучение структуры льдов Антарктиды и Скандинавии, чтобы установить правильность высказанного предположение о причине массовых заморов пресноводных организмов в условиях потепления.
Озон-хорошо или плохо?
1. Л.А. Надточий, О.Ю. Орлова. Инновации в биотехнологии. Университет ИТМО Санкт-Петербург, 2015
2. Материалы Четвертой конференции «Математическое моделирование в экологии» ЭкоМатМод-2015, г. Пущино, Россия
3. Недетерминированные модели в химических технологиях и биотехнологии: научно-методическая разработка. / Сост. – автор О.Н. Чечина. – Самара: Сам.гос. техн. ун-т, 2016. – 153 с.
4. Чечина О.Н. Биотехнологии в Самарском регионе: Монография в 2-х ч. Ч.І. Концепция биотехнологий. Этапы обучения.Ч.ІІ. Практические биотехнологии и методики. – Самара: Изд-во Сам ГТУ, 2014. – 90 с.
2. Моделирование в биологии
2.1. Методы моделирования активного эксперимента
2. 2 Моделирование –метод эколого-биологических исследований
2.3. Математические модели биологических объектов, явлений и процессов