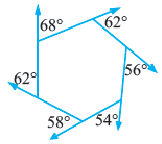
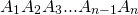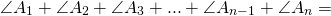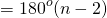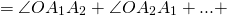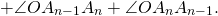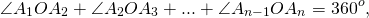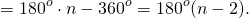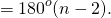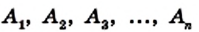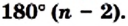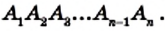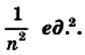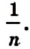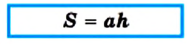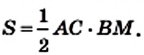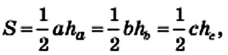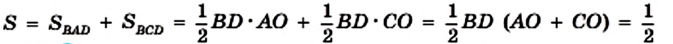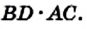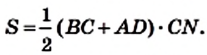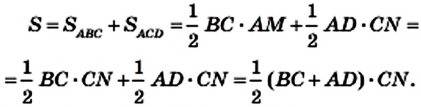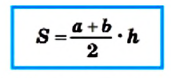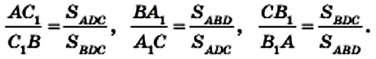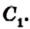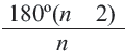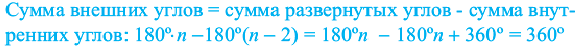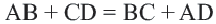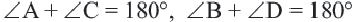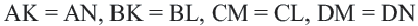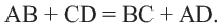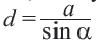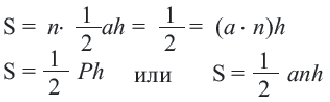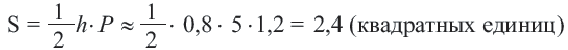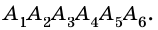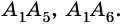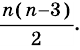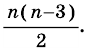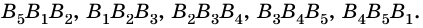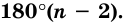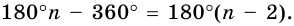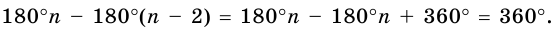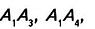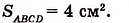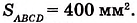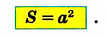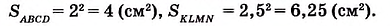Что означает формула 180 n 2

Сумма углов многоугольника

(о сумме углов выпуклого многоугольника)

Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).

(n — количество сторон многоугольника).

Другой вариант формулировки этой теоремы:

Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).

1-й способ

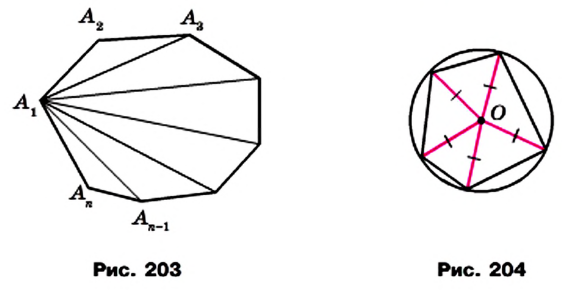
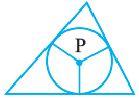
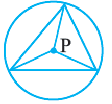
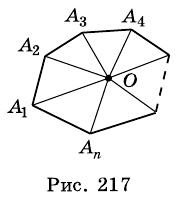
Обозначим внутри многоугольника произвольную точку O.

Соединим точку O с вершинами многоугольника.

Получили n треугольников.

Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.

Так как сумма углов при вершине O составляет 360º

то сумма углов многоугольника равна сумме углов n треугольников минус 360º.

Таким образом, искомая сумма углов n угольника равна

2-й способ

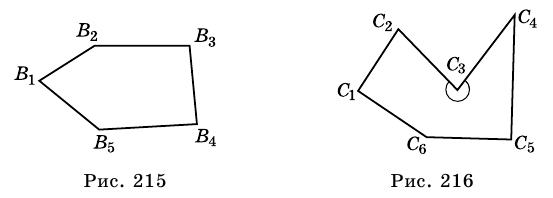
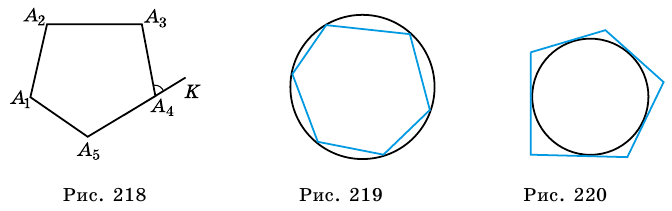
Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.

Сумма всех углов этих треугольников равна сумме углов многоугольника.

Сумма углов углов каждого из треугольников равна 180º.

Следовательно, сумма углов многоугольника

Что и требовалось доказать.

4 Comments

Нужно либо поменять название статьи, либо добавить в текст информацию о невыпуклых многоугольниках.
А так сайт оказался полезным, спасибо!

Ольга, спасибо. Подкорректирую в июне.

Очень хороший сайт! Давно им пользуюсь. Спасибо за Ваш труд!

Источник

Сумма углов n угольника

Описание презентации по отдельным слайдам:

Описание слайда:

Сумма углов n-угольника
Теорема. Сумма углов выпуклого n-угольника равна 180o(n-2).
Доказательство. Из какой-нибудь вершины выпуклого n-угольника проведем все его диагонали. Тогда n-угольник разобьется на n-2 треугольника. В каждом треугольнике сумма углов равна 180о, и эти углы составляют углы n-угольника. Следовательно, сумма углов n-угольника равна 180о(n-2).

Описание слайда:

Второй способ доказательства
Теорема. Сумма углов выпуклого n-угольника равна 180o(n-2).
Доказательство 2. Пусть O какая-нибудь внутренняя точка выпуклого n-угольника A1…An. Соединим ее с вершинами этого многоугольника. Тогда n-угольник разобьется на n треугольников. В каждом треугольнике сумма углов равна 180о. Эти углы составляют углы n-угольника и еще 360о. Следовательно, сумма углов n-угольника равна 180о(n-2).

Описание слайда:

Упражнение 1
Чему равна сумма углов выпуклого: а) 4-угольника; б) 5-угольника; в) 6-угольника?
Ответ: а) 360о;
б) 540о;
в) 720о.

Описание слайда:

Упражнение 2
Чему равен внешний угол правильного: а) 3-угольника; б) 4-угольника; в) 5-угольника; г) 6-угольника?
Ответ: а) 120о;
б) 90о;
в) 72о;
г) 60о.

Описание слайда:

Описание слайда:

Упражнение 4
Чему равны углы правильного: а) треугольника; б) четырехугольника; в) пятиугольника; г) шестиугольника; д) восьмиугольника; е) десятиугольника; ж) двенадцатиугольника?
Ответ: а) 60о;
б) 90о;
в) 108о;
г) 120о;
д) 135о;
е) 144о;
ж) 150о.

Описание слайда:

Упражнение 5
Сумма трех углов выпуклого четырехугольника равна 300о. Найдите четвертый угол.
Ответ: 60о.

Описание слайда:

Упражнение 6
Углы выпуклого четырехугольника пропорциональны числам 1, 2, 3, 4. Найдите их.
Ответ: 36о, 72о, 108o, 144o.

Описание слайда:

Описание слайда:

Упражнение 8
Сумма углов выпуклого многоугольника равна 900o. Сколько у него сторон?
Ответ: 7.

Описание слайда:

Упражнение 9
Сколько сторон имеет правильный многоугольник, если каждый из его внешних углов равен: а) 36o; б) 24o?
Ответ: а) 10;
б) 15.

Описание слайда:

Упражнение 10
Чему равна сумма углов невыпуклого четырехугольника ABCD?
Ответ: 360о.

Описание слайда:

Упражнение 11*
Найдите сумму углов 1, 2, 3, 4, 5 пятиугольной звездочки, изображенной на рисунке.
Ответ: 180о.

Описание слайда:

Упражнение 12*
Какое наибольшее число острых углов может иметь выпуклый n-угольник?
Решение. Так как сумма внешних углов выпуклого многоугольника равны 360о, то у выпуклого многоугольника не может быть более трех тупых углов, следовательно, у него не может быть более трех внутренних острых углов.
Ответ. 3.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Курс профессиональной переподготовки

Охрана труда

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Цилиндры и цилиндрические поверхности

Введение в логику

Портреты учёных математиков

Прямая пропорциональность

Вычисление объема прямоугольного параллелепипеда

Пропорциональность величин

Стандартный вид многочлена

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5398855 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования

Время чтения: 2 минуты

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Совфед отклонил закон о верифицированных онлайн-платформах и учебниках

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Правильный многоугольник

Формулы, признаки и свойства правильного многоугольника

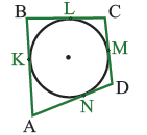
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

α 1 = α 2 = α 3 = … = α n-1 = α n

где a₁ … a_n — длины сторон правильного многоугольника,
α ₁ … α _n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

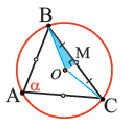
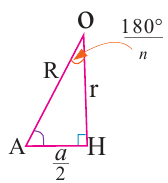
Формула стороны правильного n-угольника через радиус вписанной окружности

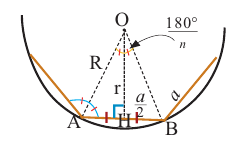
a = 2 · r · tg 180° n (через градусы),

a = 2 · r · tg π n (через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2 · R · sin 180° n (через градусы),

a = 2 · R · sin π n (через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a : 2 · tg 180° n (через градусы),

r = a : 2 · tg π n (через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a : 2 · sin 180° n (через градусы),

R = a : 2 · sin π n (через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

Формула площади n-угольника через радиус вписанной окружности

Формула площади n-угольника через радиус описанной окружности

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

Формула площади правильного треугольника через длину стороны

Формула площади правильного треугольника через радиус вписанной окружности

Формула площади правильного треугольника через радиус описанной окружности

Углы между сторонами правильного треугольника

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

Углы между сторонами правильного четырехугольника

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через радиус вписанной окружности

Формула площади правильного шестиугольника через радиус описанной окружности

Углы между сторонами правильного шестиугольника

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

Источник

Правильный многоугольник

Многоугольник представляет плоскую замкнутую геометрическую фигуру, у которой может быть три, четыре и более сторон, пересекающихся в трех, четырех и более точках, называющихся вершинами. Называются они в соответствии с количеством сторон или вершин. Например, многоугольник с пятью сторонами называется пятиугольник, с шестью — шестиугольник и т. д. Правильным называют многоугольник с равными углами и сторонами. Например, квадрат. Если в задании известна одна из этих величин, несложно узнать остальные. В равностороннем n-угольнике, сумма всех углов рассчитывается как:

(n — 2) 180°

а сумма всех его сторон будет равна:

P = na

P — периметр;
а — сторона;
n — количество сторон.

Определяем угол правильного n-угольника:

А = (n — 2) / n х 180°

a = 2 r · tg · 180° / n

a = 2 r · tg · π / n

Если задан радиус ® описанной окружности, то находим сторону по формуле:

a = 2 R · sin · 180° / n

a = 2 R · sin · π / n

Соответственно, если известна сторона правильного n-угольника, находим r вписанной окружности:

r = a / ( 2 tg · 180° / n)

r = a / ( 2 tg · π / n)

и R описанной окружности n-угольника по его стороне:

R= a / ( 2 sin · 180° / n)

R= a / ( 2 sin · π / n)

Онлайн калькулятор поможет вам быстро и правильно определить число и величину сторон правильного многоугольника, размер его внешнего и внутреннего углов, а также другие показатели.

Источник

Содержание:

Изучив материал этой лекции, вы узнаете формулу, с помощью которой можно найти сумму углов выпуклого многоугольника.

Определение многоугольников

Рассмотрим фигуру, состоящую из точек

Фигура, образованная этими отрезками, ограничивает часть плоскости, выделенную на рисунке 195 зеленым цветом. Эту часть плоскости вместе с отрезками называют многоугольником. Точки называют вершинами многоугольника, а указанные выше отрезки — сторонами многоугольника.

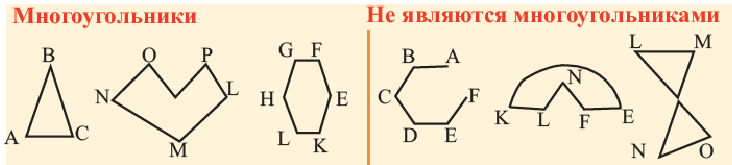
Стороны, являющиеся соседними отрезками, называют соседними сторонами многоугольника. Вершины, являющиеся концами одной стороны, называют соседними вершинами многоугольника.

Две соседние стороны многоугольника образуют угол многоугольника. Например, на рисунке 196 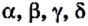— углы многоугольника, а не является углом многоугольника.

Многоугольник называют по количеству его углов: треугольник, четырехугольник, пятиугольник и т. п.

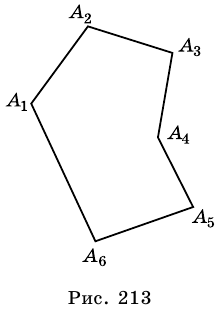
Многоугольник обозначают по его вершинам. Например, на рисунке 197 изображен пятиугольник ABCDE. В обозначении многоугольника буквы, стоящие рядом, соответствуют соседним вершинам. Например, пятиугольник, изображенный на рисунке 197, можно обозначить еще и так: CDEAB, EABCD, EDCBA и т. д.

Периметром многоугольника называют сумму длин всех его сторон.

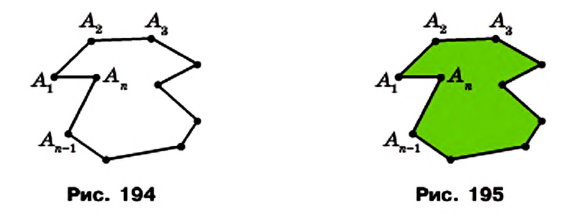
Отрезок, соединяющий несоседние вершины многоугольника, называют диагональю. Например, на рисунке 198 отрезок АЕ — диагональ шестиугольника ABCDEF.

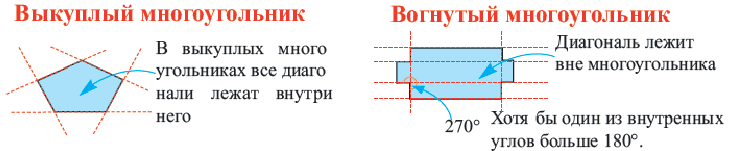
На рисунке 199 изображен многоугольник, все углы которого меньше развернутого. Такой многоугольник называют выпуклым. Из сказанного следует, что любой треугольник является выпуклым многоугольником. Заметим, что многоугольники, изображенные на рисунках 196-198, не являются выпуклыми.

Выпуклый многоугольник обладает такими свойствами:

Если многоугольник не является выпуклым, то он такими свойствами не обладает (рис. 198, 202).

Теорема 19.1. Сумма углов выпуклого n-угольника равна

Доказательство. Для случая n = 3 теорема была доказана в 7 классе (теорема 16.1).

Пусть 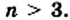На рисунке 203 изображен выпуклый n-угольник

Докажем, что сумма всех его углов равна 180° (n-2).

Отметим, что эта теорема справедлива и для любого многоугольника, не являющегося выпуклым.

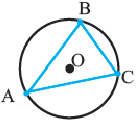
Определение. Окружность называют описанной около многоугольника, если она проходит через все его вершины.

На рисунке 204 изображена окружность, описанная около многоугольника. В этом случае также говорят, что многоугольник вписан в окружность.

Центр окружности, описанной около многоугольника, равноудален от всех его вершин. Следовательно, этот центр принадлежит серединным перпендикулярам всех сторон многоугольника, вписанного в окружность.

Около многоугольника можно описать окружность, если существует точка, равноудаленная от всех его вершин. Следовательно, если серединные перпендикуляры всех сторон многоугольника пересекаются в одной точке, то около такого многоугольника можно описать окружность.

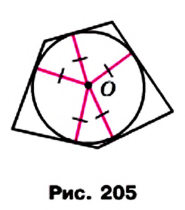
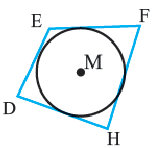
Определение. Окружность называют вписанной в многоугольник, если она касается всех его сторон.

На рисунке 205 изображена окружность, вписанная в многоугольник. В этом случае также говорят, что многоугольник описан около окружности.

Центр окружности, вписанной в многоугольник, равноудален от всех его сторон. Следовательно, этот центр принадлежит биссектрисам всех углов многоугольника, описанного около окружности.

Понятие площади многоугольника. Площадь прямоугольника

С такой величиной, как площадь, вы часто встречаетесь в повседневной жизни: площадь квартиры, площадь дачного участка, площадь поля и т. п.

Опыт подсказывает вам, что равные земельные участки имеют равные площади, что площадь квартиры равна сумме площадей всех ее помещений (комнат, кухни, коридора и т. д.).

Вы знаете, что площади земельных участков измеряют в сотках (арах) и гектарах; площади регионов и государств — в квадратных километрах; площадь квартиры — в квадратных метрах.

На этих практических знаниях о площади основывается определение площади многоугольника.

Определение. Площадью многоугольника называют положительную величину, которая обладает следующими свойствами:

Измерить площадь многоугольника — это значит сравнить его площадь с площадью единичного квадрата. В результате получают числовое значение площади данного многоугольника. Это число показывает, во сколько раз площадь данного многоугольника отличается от площади единичного квадрата.

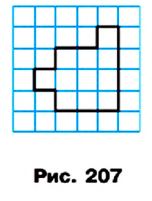
Например, если клетку вашей тетради принять за единичный квадрат, то площадь многоугольника, изображенного на рисунке 207, будет равна 11 квадратным единицам (кратко записывают: 11 ед. 2 ).

Обычно для нахождения площади используют формулы, то есть вычисляют площадь многоугольника по определенным элементам (сторонам, диагоналям, высотам и т. д.). Некоторые из формул вы уже знаете. Например, вы неоднократно применяли формулу S = ab, где S — площадь прямоугольника, а и b — длины его соседних сторон.

Для доказательства этой формулы потребуется следующая лемма.
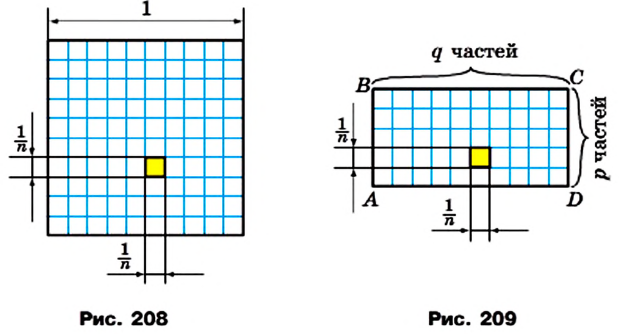
Лемма. Площадь квадрата со стороной 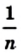ед. (n — натуральное число) равна

Теорема 20.1. Площадь прямоугольника равна произведению длин его соседних сторон.

Доказательство. На рисунке 209 изображен прямоугольник ABCD, длины соседних сторон которого равны a и b: АВ = а, ВС = b. Докажем для случая, когда а и b — рациональные числа, что площадь S прямоугольника вычисляют по формуле S = ab.

Числа а и b представим в виде обыкновенных дробей с одинаковыми знаменателями:
где — натуральные числа.
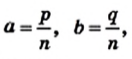
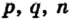
Разделим сторону АВ на р равных частей, а сторону ВС — на q равных частей. Через точки деления проведем прямые, параллельные сторонам прямоугольника. Тогда прямоугольник будет разделен на 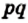равных квадратов со стороной

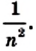
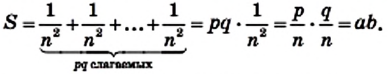
Согласно лемме площадь каждого квадрата равна Из определения площади (свойство 2) следует, что площадь прямоугольника равна сумме площадей всех квадратов, то есть
Рассмотрение случая, когда хотя бы одно из чисел а или b является иррациональным, выходит за рамки школьного курса геометрии.

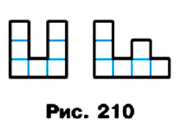
Определение. Многоугольники, имеющие равные площади, называют равновеликими.

Из определения площади (свойство 1) следует, что все равные фигуры равновелики. Однако не все фигуры, имеющие равные площади, являются равными. Например, на рисунке 210 изображены два многоугольника, каждый из которых составлен из семи единичных квадратов. Эти многоугольники равновелики, но не равны.

Площадь параллелограмма

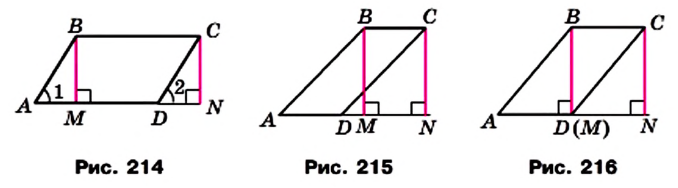
Теорема 21.1. Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.

Доказательство. На рисунке 214 изображены параллелограмм ABCD, площадь которого равна S, и его высота ВМ. Докажем, что S = ВС • ВМ.

Проведем высоту CN. Легко показать (сделайте это самостоятельно), что четырехугольник MBCN — прямоугольник. Покажем, что он равновелик данному параллелограмму.

Площадь параллелограмма равна сумме площадей треугольника АВМ и трапеции MBCD. Площадь прямоугольника равна сумме площадей указанной трапеции и треугольника DCN. Однако треугольники АВМ и DCN равны по гипотенузе и острому углу (отрезки АВ и CD равны как противолежащие стороны параллелограмма, углы 1 и 2 равны как соответственные при параллельных прямых АВ и DC и секущей AD). Значит, эти треугольники равновелики. Отсюда следует, что параллелограмм ABCD и прямоугольник MBCN равновелики.

По теореме 20.1 площадь прямоугольника MBCN равна произведению длин сторон ВС и ВМ. Тогда S = ВС • ВМ, где S — площадь параллелограмма ABCD.

Для завершения доказательства надо рассмотреть случаи, когда основание М высоты ВМ не будет принадлежать стороне AD (рис. 215) или совпадет с вершиной D (рис. 216). И в этом случае параллелограмм ABCD и прямоугольник MBCN будут равновеликими. Докажите этот факт самостоятельно.

Если обозначить длины стороны параллелограмма и проведенной к ней высоты соответственно буквами а и h, то площадь S параллелограмма вычисляют по формуле

Площадь треугольника

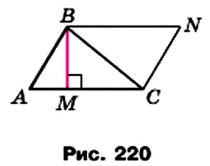
Теорема 22.1. Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.

Доказательство. На рисунке 220 изображены треугольник АВС, площадь которого равна S, и его высота ВМ. Докажем, что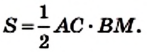
Через вершины В и С треугольника проведем прямые, параллельные сторонам АС и АВ соответственно (рис. 220). Пусть эти прямые пересекаются в точке N. Четырехугольник ABNC — параллелограмм по определению. Треугольники АВС и NCB равны (докажите это самостоятельно). Следовательно, равны и их площади. Тогда площадь треугольника АВС равна половине площади параллелограмма ABNC. Высота ВМ треугольника АВС является также высотой параллелограмма
ABNC. Отсюда

Если воспользоваться обозначениями для высот и сторон треугольника АВС, то согласно доказанной теореме имеем:

где S — площадь треугольника.

Следствие. Площадь прямоугольного треугольника равна половине произведения его катетов.

Докажите эту теорему самостоятельно.

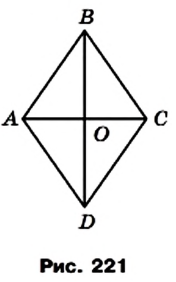
Пример №1

Докажите, что площадь ромба равна половине произведения его диагоналей.

Решение:

На рисунке 221 изображен ромб ABCD, площадь которого равна S. Его диагонали АС и BD пересекаются в точке О. Докажем, что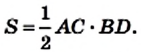
Поскольку диагонали ромба перпендикулярны, то отрезки АО и СО являются высотами треугольников BAD и BCD соответственно. Тогда можно записать:

Площадь трапеции

Теорема 23.1. Площадь трапеции равна произведению полусуммы ее оснований и высоты.

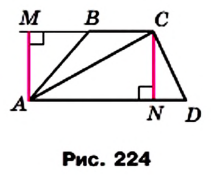
Доказательство. На рисунке 224 изображена трапеция ABCD (AD||BC), площадь которой равна S. Отрезок CN — высота этой трапеции. Докажем, что

Проведем диагональ АС и высоту AM трапеции. Отрезки AM и CN являются высотами треугольников АВС и ACD соответственно.

Имеем:

Если обозначить длины оснований трапеции и ее высоты соответственно буквами 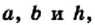то площадь S трапеции вычисляют по формуле

Следствие. Площадь трапеции равна произведению ее средней линии и высоты.

Равносоставленные и равновеликие многоугольники

Если некоторый многоугольник можно разрезать на части и составить из них другой многоугольник, то такие два многоугольника называют равносоставленными.

Например, если прямоугольник разрезать вдоль его диагонали (рис. 228), то получим два равных прямоугольных треугольника, из которых можно составить равнобедренный треугольник (рис. 229). Фигуры на рисунках 228 и 229 — равно составленные.

Очевидно, что равносоставленные многоугольники являются равновеликими. Этот факт применяют при доказательстве теорем и решении задач. Например, доказывая теорему 21.1, мы фактически разрезали параллелограмм на треугольник АВМ и трапецию MBCD, из которых составили прямоугольник MBCN (см. рис. 215).

Если треугольник разрезать вдоль средней линии, то из полученных треугольника и трапеции можно составить параллелограмм (рис. 230).

Легко установить (сделайте это самостоятельно), что такое разрезание треугольника приводит к еще одному доказательству теоремы о площади треугольника (теорема 22.1). Этой же цели служит разрезание треугольника на части, из которых можно составить прямоугольник (рис. 231).

Евклид в своей знаменитой книге «Начала» формулирует теорему Пифагора так:

«Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах».

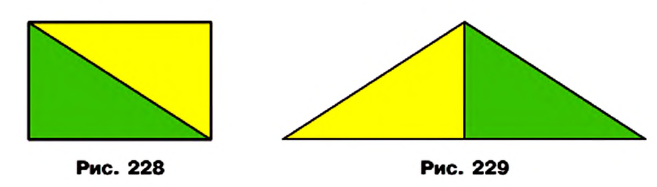
Если показать, что можно разрезать квадраты, построенные на катетах, на части и составить из этих частей квадрат со стороной, равной гипотенузе, то тем самым будет доказана теорема Пифагора.

На рисунке 232 показан один из возможных способов такого разрезания. Квадраты, построенные на катетах, разрезаны на части, площади которых равны 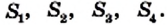Из этих частей сложен квадрат, построенный на гипотенузе.

Из определения площади многоугольника следует, что равносоставленные многоугольники являются равновеликими. Но совсем неочевидной является такая теорема.

Теорема. Любые два равновеликих многоугольника являются равносоставленными.

Впервые этот факт доказал в 1832 г. венгерский математик Фаркаш Бойяи. Позднее немецкий математик Пауль Гервин нашел другое доказательство. Поэтому эту теорему называют теоремой Бойяи—Гервина.

Теорема Чевы

На сторонах ВС, СА и АВ треугольника АВС отметим произвольные точки 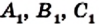(рис. 234). Каждый из отрезков АЛ,, BBV СС, называют чевианой треугольника АВС. Такое название связано с именем итальянского инженера и математика Джованни Чевы (1648-1734), открывшего удивительную теорему.

Если точки 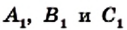выбраны так, что чевианы являются биссектрисами, либо медианами, либо высотами остроугольного треугольника, то эти чевианы пересекаются в одной точке.

Если три прямые пересекаются в одной точке, то их называют конкурентными.

Теорема Чевы дает общий критерий конкурентности произвольных трех чевиан.

Теорема. Для того чтобы, чевианы 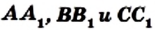треугольника АВС пересекались в одной точке, необходимо и достаточно, чтобы выполнялось равенство

Доказательство. Докажем сначала необходимое условие конкурентности: если чевианы 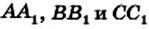пересекаются в одной точке, то выполняется равенство (*).

Воспользовавшись результатом ключевой задачи 757, можно записать (рис. 235):

Перемножив записанные равенства, получим равенство (*).

Докажем теперь достаточное условие конкурентности: если выполняется равенство (*), то чевианы 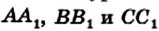пересекаются в одной точке.

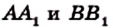
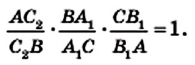
Пусть чевианы пересекаются в точке D, а чевиана, проходящая через вершину С и точку D, пересекает сторону АВ в некоторой точке Из доказанного выше можно записать:

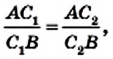
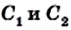
Сопоставляя это равенство с равенством (*), приходим к выводу, что то есть точки делят отрезок АВ в одном и том же отношении, а значит, эти точки совпадают. Следовательно, прямая CD пересекает сторону АВ в точке

Напомню:

Окружность, описанная около многоугольника
Окружность называют описанной около многоугольника, если она проходит через все его вершины.

Окружность, вписанная в многоугольник
Окружность называют вписанной в многоугольник, если она касается всех его сторон.

Площадь многоугольника
Площадью многоугольника называют положительную величину,
которая обладает следующими свойствами:

Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон.

Равновеликие многоугольники
Многоугольники, имеющие равные площади, называют равновеликими.

Площадь параллелограмма
Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.

Площадь треугольника
Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.

Площадь прямоугольного треугольника
Площадь прямоугольного треугольника равна половине произведения его катетов.

Площадь трапеции

Ломанная линия и многоугольники

Многоугольник называется правильным, если у него все стороны все углы конгруэнтны.

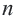
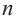
В многоугольнике количество вершин, сторон и углов одинаковые. Многоугольник с — сторонами называют еще и — угольным.

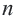
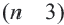
Соответственно количеству сторон, многоугольники называются треугольными, четырехугольными, пятиугольными, шестиугольными т.д. Из любой вершины выпуклого — угольника выходят диагонали.

Внутренние и внешние углы многоугольника

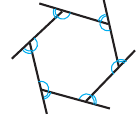
Угол, образованный двумя сторонами, исходящими из данной вершины называется внутренним углом при данной’ вершине выпуклого многоугольника. Угол, смежный с внутренним углом многоугольника называется внешним. Сумма внутренних и внешних углов (взятых по одному при каждой вершине) многоугольника при любой вершине равна .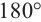

Теорема 1. Сумма внутренних углов выкуплого 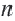— угольника равна .

Следствие: Каждый внутренний угол правильного 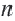— угольника равен

Теорема 2. Сумма внешних углов выкуплого многоугольника равен .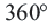

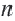
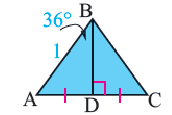
Следствие 2. Каждый внешний угол правильного — угольника равен .

Пример №2

Один из внешних углов правильного многоугольника равен .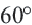

a) найдите градусную меру внутреннего угла многоугольника;

b) найдите число сторон многоугольника.

Решение: а) ;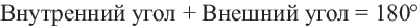

Внутренний угол:

b)

Многоугольники вписанные в окружность и описанные около окружности

Определение 1. Многоугольник называется вписанным в окружность, если все его вершины лежат на окружности, а окружность называется описанной около многоугольника. На рисунке треугольник вписан в окружность.

Определение 2. Многоугольник называется описанным около окружности, если все его стороны касаются окружности, а окружность называется вписанной в многоугольник. На рисунке четырехугольник описан около окружности.

Окружность, вписанная в треугольник и описанная около нее

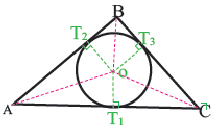
Теорема 1. В любой треугольник можно вписать окружность. Центром этой окружности будет точка пересечения биссектрис углов треугольника.

Теорема 2. Около любого треугольника можно описать окружность. Центром этой окружности будет точка пересечения серединных перпендикуляров к сторонам треугольника.

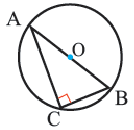
Теорема 3. Если в окружность вписан прямоугольный треугольник, то гипотенуза является диаметром этой окружности.

Доказательство 1-ой теоремы (текстовое). Проведем биссектрисы углов и треугольника и точку пересечения обозначим буквой . Произвольная точка, взятая на биссектрисе находится на одинаковом расстоянии от сторон угла. Поэтому Точка находится и на биссектрисе угла (почему?). Нарисуем окружность с центром в точке и радиусом Так как стороны треугольника перпендикулярны радиусам то в точках они касаются окружности. А значит, эта окружность является вписанной в треугольник.

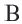
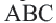
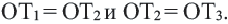
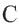
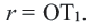
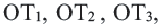
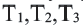
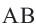
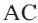
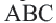
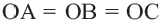
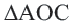
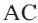
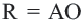
Доказательство 2-ой теоремы. Через середины сторон и треугольника проведем перпендикуляры и точку их пересечения обозначим буквой . По свойству серединного перпендикуляра к отрезку . Так как равнобедренный, то точка находится и на серединном перпендикуляре стороны . Окружность с центром в точке и радиусом , пройдя через все вершины треугольника, будет описанной около нее.

Замечание: Около данного треугольника можно описать только одну окружность. В данную окружность можно вписать бесконечное количество треугольников.

Свойства четырехугольников, вписанных в окружность и описанного около нее

В отличие от треугольников, не во всякий четырехугольник можно вписать или описать окружность.

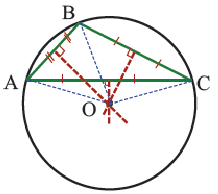
Теорема 4. В любом описанном четырехугольнике суммы противоположных сторон равны.

Обратная теорема. Если суммы противоположных сторон четырехугольника равны, то в этот четырехугольник можно вписать окружность.

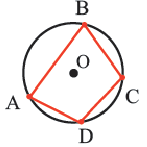
Теорема 5. Сумма двух противоположных углов четырехугольника, вписанного в окружность, равна

Обратная теорема. Если сумма противоположных углов четырехугольника равна 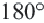, то около этого четырехугольника можно описать окружность.

Доказательство теоремы 4: Пусть точки 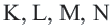будут точками касания сторон четырехугольника. По свойству касательных, проведенных из данной точки к окружности,

Если сложить почленно эти равенства, получим 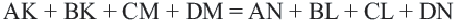или же

Отношение стороны треугольника, вписанного в окружность, к синусу противолежащего угла равно диаметру этой окружности:

Исследуйте данное доказательство для случая, когда центр окружности расположен внутри треугольника, обсудите и напишите в тетради.

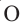
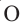
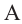
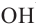
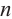
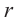
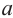
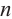
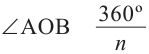
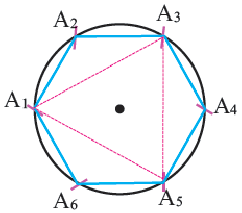
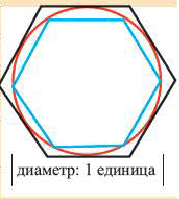
В любой правильный многоугольник можно вписать и описать окружность. Центры этих окружностей совпадут. Биссектрисы углов правильного многоугольника пересекаются в точке и образуют равнобедренные треугольники конгруэнтные показанному на рисунке (по признаку УСУ). Нарисуем окружность радиусом с центром в точке . Эта окружность, пройдя через все вершины, будет описанной окружностью. окружность с радиусом , касаясь всех сторон многоугольника, будет вписанной окружностью. — радиус окружности, описанной около правильного -угольника, -радиус вписанной окружности, -сторона правильного -угольника, — центральный угол

Задача на построение: Постройте правильный шестиугольник.

1. Нарисуйте отрезок , равный стороне правильного шестиугольника.

2. Циркулем нарисуйте окружность, радиус которой равен длине этого отрезка.

3. Не меняя раствора циркуля, разбейте всю окружность на части одинаковой длины и отметьте их точками.

4. Соедините последовательно отмеченные точки. Получится правильный шестиугольник, вписанный в окружность.

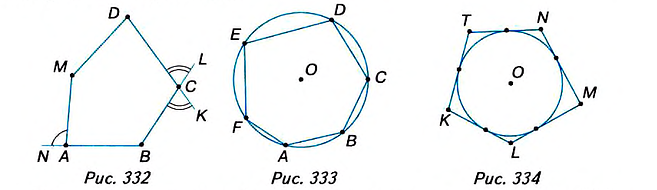
Если соединить попарно некоторые вершины правильного шестиугольника , например, вершины , то получится правильный треугольник. Чтобы построить правильный четырехугольник, нужно провести два взаимно перпендикулярных диаметра и последовательно соединить их концы. Если в окружность вписан правильный — угольник, то отметив точки пересечения серединных перпендикуляров с окружностью, получим точки являющиеся вершинами правильного -угольника.

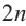
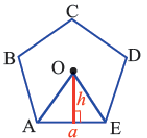
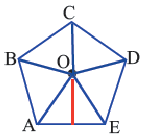
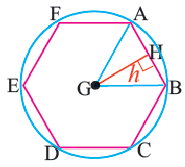
Площадь правильного многоугольника

Центр правильного многоугольника. Центр окружности, описанного около правильного многоугольника или вписанного в него, является центром правильного многоугольника. Центр правильного многоугольника находится на одинаковом расстоянии от всех вершин и всех сторон многоугольника.

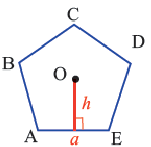
Апофема правильного многоугольника. Перпендикуляр, проведенный из центра многоугольника к его стороне, называется апофемой. Апофема правильного многоугольника равна радиусу вписанной окружности.

Выполните следующее упражнение по шагам и выведите формулу зависимости площади правильного многоугольника от апофемы.

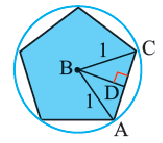
1. Нарисуйте правильный пятиугольник .

2. Из центра проведите перпендикуляр, делящий сторону пополам.

3. Соедините точки и с центром .

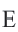
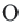
4. Выразите площадь треугольника переменными и . Обратите внимание какому измерению многоугольника соответствует высота треугольника.

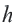
5. Соедините точки с точкой . Сравните площади полученных треугольников.

6. Обратите внимание на то, что площадь пятиугольника равна сумме площадей этих треугольников. Площадь пятиугольника:

7. Какому измерению соответствует выражение ? Выразите площадь пятиугольника через его периметр.

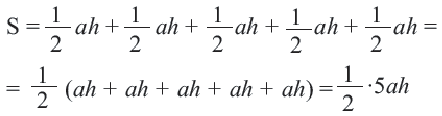
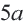
Площадь правильного многоугольника:

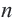
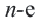
Соединив центр правильного -угольника с вершинами, получится количество равнобедренных конгруэнтных треугольников.

Пример №3

В окружность радиусом равным единице, вписан правильный пятиугольник. Найдите площадь пятиугольника. Решение:

Площадь многоугольника:

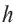
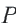
Нужно найти апофему и периметр .

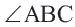
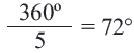
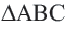
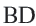
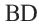
Центральный угол равен . — равнобедренный треугольник, а значит его высота является и медианой, и биссектрисой.

— апофема пятиугольника,

Сторона пятиугольника:

1. Принимая за единицу диаметр окружности, найдите периметр вписанного шестиугольника.

2. Покажите, что длина окружности с единичным диаметром равна .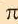

3. Нарисуйте радиус окружности. Найдите периметр описанного шестиугольника.

4. Напишите неравенство: .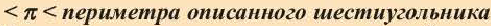

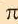
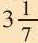
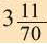
Увеличив число сторон многоугольника в 2 раза и продолжая вычисления для 12-ти, а затем для 96-ти угольного многоугольника Архимед, определил, что значения больше , но меньше .

Паркетирование

Паркетированием называется покрытие площади фигурами до заполнения всей пустоты.

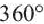
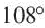
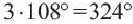
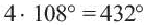
Если сумма углов при общей вершине многоугольника равна , то паркетированием можно покрыть всю пустую часть площади. Паркетирование возможно при помощи правильных треугольников, ромбов (квадратов) и правильных шестиугольников. Однако, при помощи правильных пятиугольников это сделать невозможно, потому что, градусная мера одного угла равна , а сумма углов при общей вершине трех пятиугольников , а четырех пятиугольников .

Справочный материал по многоугольникам

Многоугольник и его элементы.

Сумма углов выпуклого многоугольника. многоугольник, вписанный в окружность, и многоугольник, описанный около окружности.

Рассмотрим фигуру изображенную на рисунке 213. Она состоит из отрезков и При этом отрезки размещены так, что соседние отрезки ( и и и ) не лежат на одной прямой, а несоседние отрезки не имеют общих точек. Такую фигуру называют многоугольником. Точки называют вершинами многоугольника, а отрезки — сторонами многоугольника.

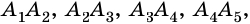
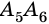
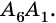
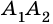
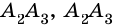
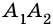
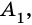
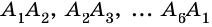
Очевидно, что количество вершин многоугольника равно количеству его сторон.

Сумму длин всех сторон многоугольника называют его периметром.

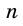
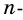
Многоугольник, у которого вершин, называют угольником. На рисунке 213 изображен шестиугольник

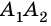
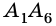
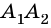
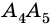
Две стороны многоугольника называют соседними, если они имеют общую вершину. Стороны многоугольника, не имеющие общей вершины, называют несоседними. Например, стороны и — соседние, a и — несоседние (рис. 213).

Две вершины многоугольника называют соседними, если они принадлежат одной стороне, а вершины многоугольника, не принадлежащие одной стороне, называют несоседними.

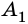
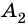
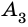
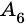
Например, вершины и — соседние, и — несоседние (рис. 213).

Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. На рисунке 214 изображены диагонали многоугольника 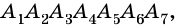выходящие из вершины

Пример №4

Сколько диагоналей имеет угольник?

Решение:

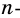
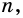
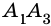
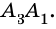
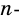
Из каждой вершины угольника выходит диагонали. Всего вершин а каждая диагональ повторяется дважды, например и Поэтому всего диагоналей у угольника будет

Ответ.

Углы, стороны которых содержат соседние стороны многоугольника, называют углами многоугольника. Пятиугольник 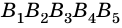имеет углы

Если каждый из углов многоугольника меньше развернутого, то такой многоугольник называют выпуклым. Если хотя бы один угол многоугольника больше развернутого, то такой многоугольник называют невыпуклым.

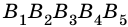
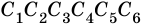
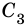
Многоугольник — выпуклый (рис. 215), а многоугольник — невыпуклый (рис. 216), так как угол при вершине больше чем 180°.

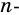
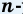
Теорема (о сумме углов выпуклого угольника). Сумма углов выпуклого угольника равна

Доказательство:

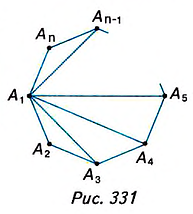
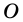
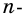
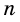
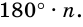
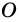
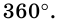
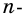
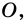
Выберем во внутренней области многоугольника произвольную точку и соединим ее со всеми вершинами угольника (рис. 217). Получим треугольников, сумма всех углов которых равна Сумма углов с вершиной в точке равна Сумма углов данного угольника равна сумме углов всех треугольников, кроме углов с вершиной в точке то есть:

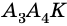
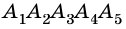
Углы выпуклого многоугольника называют еще его внутренними углами. Угол, смежный с внутренним углом многоугольника, называют внешним углом многоугольника. На рисунке 218 угол — внешний угол многоугольника — при вершине

Очевидно, что каждый многоугольник имеет по два внешних угла при каждой вершине.

Пример №5

Докажите, что сумма внешних углов выпуклого 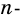угольника, взятых по одному при каждой вершине, равна 360°.

Решение:

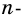
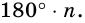
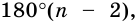
Сумма внутреннего и внешнего углов при каждой вершине многоугольника равна 180°. Поэтому сумма всех внутренних и внешних углов угольника равна Так как сумма внутренних углов равна то сумма внешних углов равна:

Многоугольник называют вписанным в окружность, если все его вершины лежат на окружности. Окружность при этом называют описанной около многоугольника (рис. 219).

Около многоугольника не всегда можно описать окружность. Если же это возможно, то центром такой окружности является точка пересечения серединных перпендикуляров к сторонам многоугольника (как и в случае треугольника).

Многоугольник называют описанным около окружности, если все его стороны касаются окружности. Окружность при этом называют вписанной в многоугольник (рис. 220).

Не в каждый многоугольник можно вписать окружность. Если же это возможно, то центром такой окружности является точка пересечения биссектрис внутренних углов многоугольника (как и в случае треугольника).

Многоугольник и его свойства

В зависимости от количества вершин (углов либо сторон) многоугольник называется треугольником, четырёхугольником, пятиугольником и т. д. Многоугольник с n вершинами называется n-угольником.

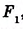
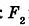
Ни одна из прямых, проходящих через стороны многоугольника не пересекает другие его стороны. Он лежит по одну сторону от любой из этих прямых. Такой многоугольник называется выпуклым. Многоугольник не является выпуклым.

В дальнейшем мы будем рассматривать лишь выпуклые многоугольники.

Периметром многоугольника называется сумма длин всех его сторон. Его обозначают буквой Р.

Диагональю n-угольника называется отрезок, который соединяет две несоседние его вершины.

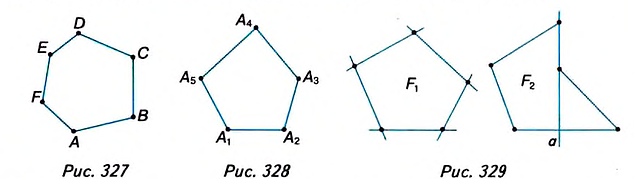
Теорема (о сумме углов n-угольника).

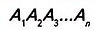
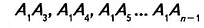
Дано: — n-угольник (рис. 331), — диагонали. Доказать:

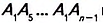
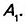
Доказательство. В заданном n-угольнике диагонали выходят из одной вершины Поэтому они разбивают n-угольник на n — 2 треугольников. Сумма всех углов образованных треугольников равна сумме углов данного n-угольника. Поскольку в каждом треугольнике сумма углов равна 180°, то сумма углов данного n-угольника — 180° • (n — 2).

Угол, смежный с углом многоугольника (рис. 332), называется внешним углом многоугольника.

Многоугольники могут быть вписанными в окружность (рис. 333) или описанными около окружности (рис. 334). Попытайтесь дать определения и сравните их с указанными в учебнике.

1. Геометрическая фигура называется простой, если её можно разбить на конечное количество треугольников. Многоугольник — это простая фигура (см. рис. 330 и 331), а окружность не является простой фигурой (рис. 337). Даже вписав в окружность многоугольник с очень большим количеством сторон, мы только приблизим его контур к окружности. Поэтому в геометрии длину окружности и площадь круга находят другими методами, чем периметр и площадь многоугольника.

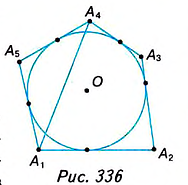
2. У вас может возникнуть вопрос: Всегда ли из равенства сторон многоугольника следует равенство его углов и наоборот? Нет, это свойство лишь треугольника. Вы знаете пример четырёхугольника, в котором все стороны равны, а углы — не равны. Это ромб. В прямоугольнике все углы равны, а вот стороны — нет. Среди многоугольников с большим количеством вершин также можно выделить равносторонние многоугольники, в которых не все углы равны (рис. 338), и равноугольные многоугольники, в которых не все стороны равны

Понятие площади

Многоугольник вместе с его внутренней областью называется плоским многоугольником.

Некоторые единицы измерения площади имеют специальные названия: ар (квадрат со стороной 10м), гектар (квадрат со стороной 100 м) и т. д.

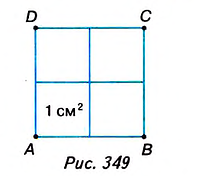
На рисунке 349 вы видите квадрат ABCD со стороной 2 см. Он состоит из четырёх квадратов площадью 1 см2, поэтому его площадь равна 4 см2.

Можем записать:

Ясно, что площадь любой фигуры выражается положительным числом. Изменится ли площадь квадрата ABCD, если за единицу измерения принять 1 мм2? Нет, площадь квадрата не изменится, но будет выражена иначе:

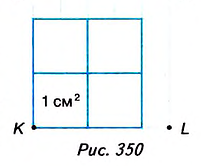
На рисунке 350 длина стороны квадрата KLMN равна 2,5 см. Он вмещает четыре квадрата площадью 1 см2 и ещё 9 маленьких квадратов площадью 0,25 см2. Поэтому 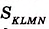= 4 + 9 • 0,25 = 6,25 (см2).

Ясно, что площадь любой фигуры равна сумме площадей частей, из которых она состоит.

Для квадратов ABCD и KLMN получим:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник