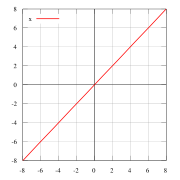
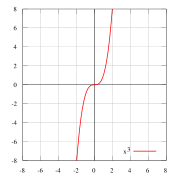
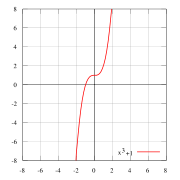
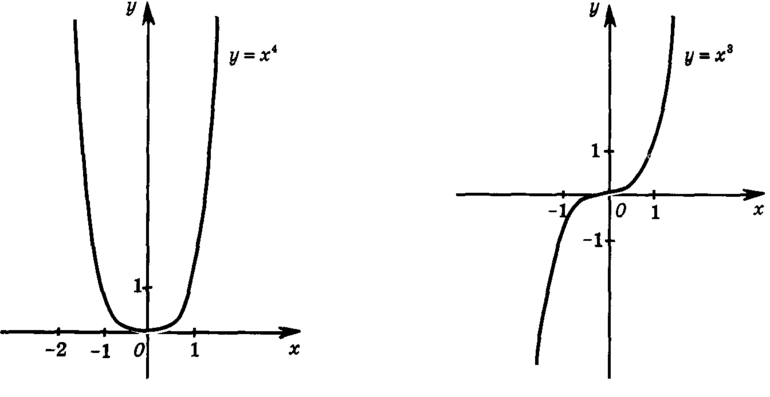Что означает что функция четная

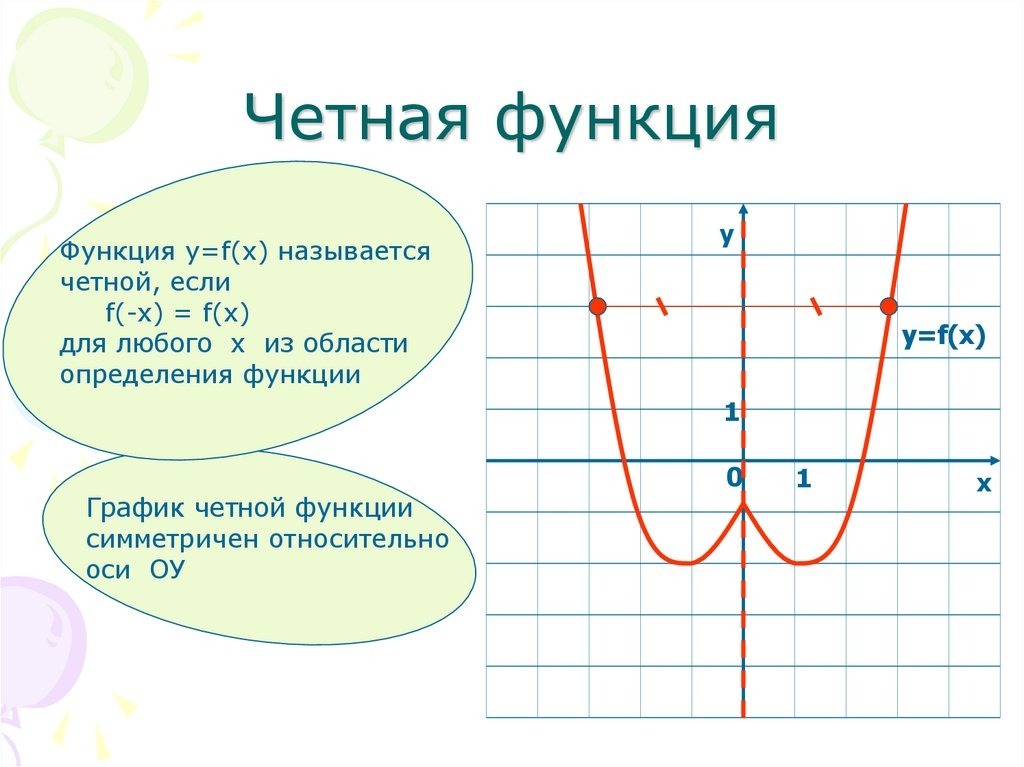
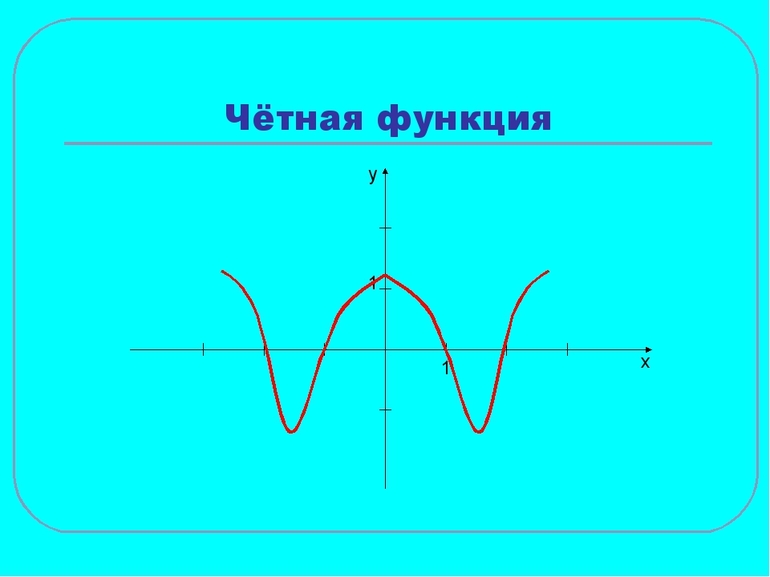
Четная функция

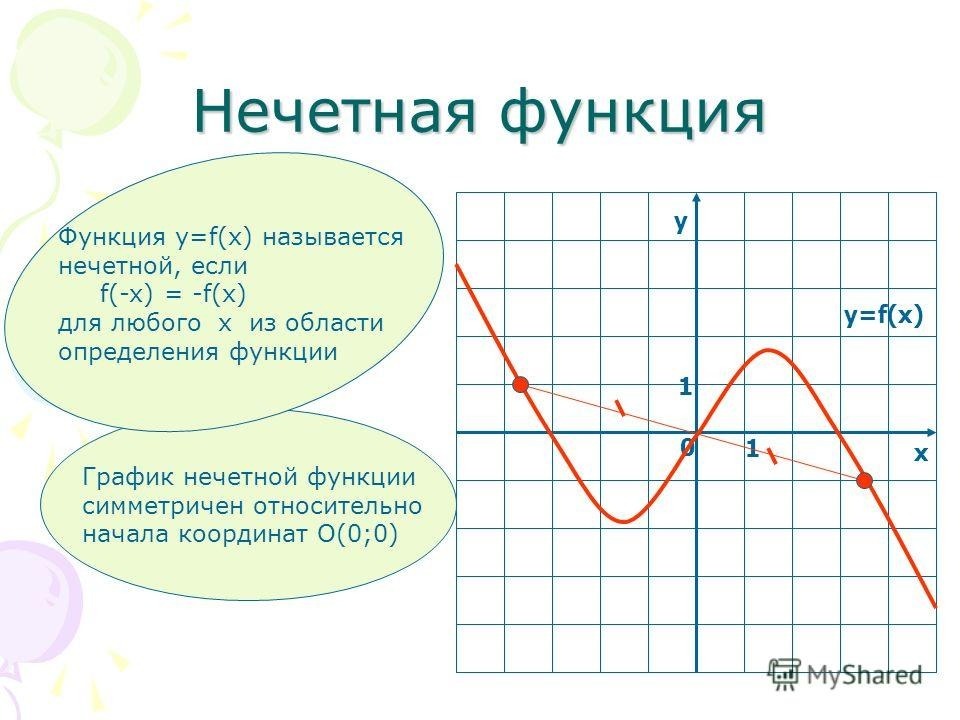
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

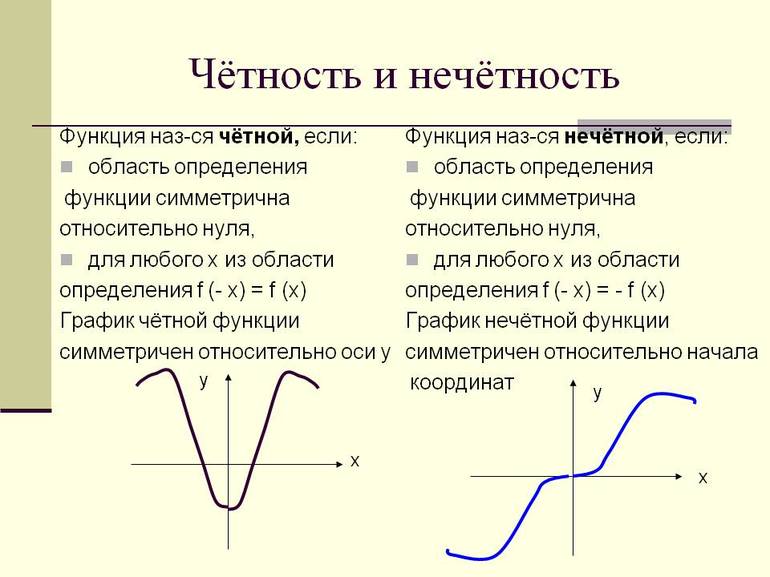
Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

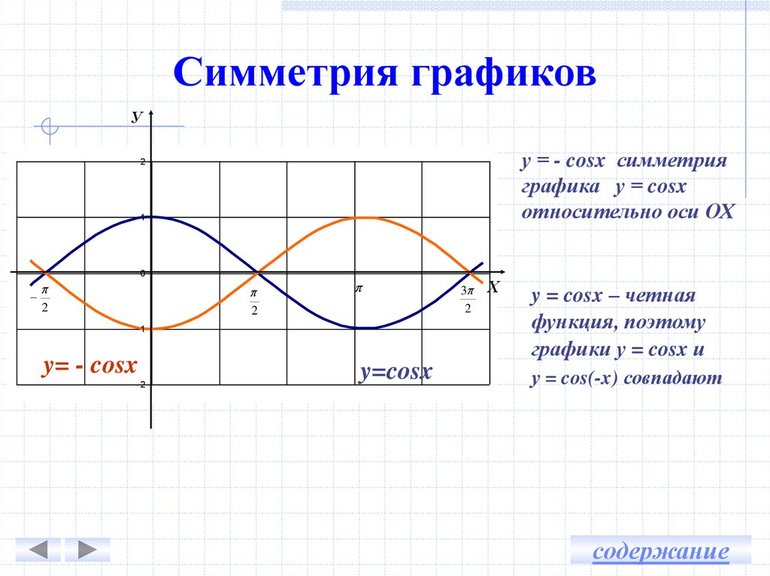
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Содержание

Определения

Свойства

Примеры

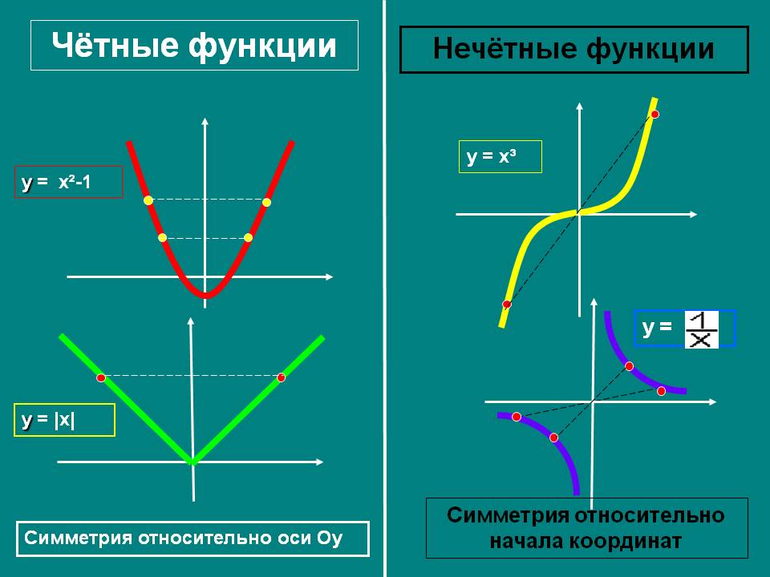
Нечётные функции

Чётные функции

Вариации и обобщения

Полезное

Смотреть что такое «Четная функция» в других словарях:

ЧЕТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех x … Большой Энциклопедический словарь

ЧЕТНАЯ ФУНКЦИЯ — функция, не меняющая знак при изменении знака независимого переменного, т. е. функция, удовлетворяющая условию f( x)=f(x). График Ч. ф. симметричен относительно оси ординат … Математическая энциклопедия

ЧЕТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех х … Естествознание. Энциклопедический словарь

чётная функция — функция, удовлетворяющая равенству f( х) = f(х) при всех х. * * * ЧЕТНАЯ ФУНКЦИЯ ЧЕТНАЯ ФУНКЦИЯ, функция, удовлетворяющая равенству f( x) = f(x) при всех x … Энциклопедический словарь

Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия

Спектральная плотность — В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье. Если процесс имеет… … Википедия

ЛЮКСЕМБУРГА НОРМА — функция где М(и) четная выпуклая функция, возрастающая при положительных U, М(u)>0 при u>0, G ограниченное замкнутое множество в Свойства этой нормы были изучены В. Люксембургом [1]. Л. н. эквивалентна норме Ор лича (см. Орлича… … Математическая энциклопедия

ВЕИЕРШТРАССА ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ — ф>тнкции, положенные К. Вейерштрассом в основу его общей теории эллиптических функций, излагавшейся им с 1862 на лекциях в Берлинском университете (см. [1], [2]). В отличие от более раннего построения теории эллиптич. функций, связанного с… … Математическая энциклопедия

Источник

Понятие четной и нечетной функции

Понятие четности и нечетности функции

Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.

Четная функция

Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

График четной функции симметричен относительно оси Ох.

Нечетная функция

Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)

График нечетной функции симметричен относительно начала координат (точки (0;0)).

Произведение четной и нечетной функции

Произведение четной и нечетной функций есть нечетная функция.

Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)

Исследование функций в примерах

Доказать, что функция \(y=x^2\) четная.

1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)

1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функции \(f_1(x)=\frac\) и \(f_2(x)=\frac4\)

Рассмотрим первую функцию:

1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.

Рассмотрим вторую функцию:

Источник

Как определить четность и нечетность функции примеры

Привет всем посетителям! Сегодня рассматриваем вопрос четности и нечетности функций.

Если , то функция четная.

Если , то функция нечетная.

При этом важно, чтобы область определения функции была бы симметричной относительно оси ординат, а при наличии в ней выколотых точек или интервалов они также должны располагаться симметрично.

Установить, симметрична ли область определения функции. Если это так, то найти и сравнить с

Если то функция — четная.
Если , то функция нечетная.

Функция совсем не обязана быть четной или нечетной, она может быть «никакой», несмотря на то, что область определения симметрична.

1. Определить, является ли четной функция: .

Область определения этой функции – все действительные числа, то есть она симметрична. Теперь подставим вместо x – (-x) и посмотрим, что получится:

– функция четна.

Надо отметить, что график четной функции симметричен относительно оси ординат, она для него словно зеркало. Поэтому графики таких функций можно строить в правой полуплоскости, а в левую просто отражать.

Верно и следующее: если функция задана графиком, который симметричен относительно оси ординат, то она четная.

2. Определить, является ли четной функция: .

Область определения этой функции может быть найдена из системы неравенств:

=0> >=0>>><>” title=”delim >=0> >=0>>><>”/>

Оба неравенства всегда соблюдаются, так как дискриминант обоих трехчленов всегда меньше 0, и ветви парабол направлены вверх – таким образом, мы установили, что область определения симметрична – это вся числовая ось.
Теперь подставим вместо x – (-x): – данная функция нечетна.

График нечетной функции симметричен относительно начала координат, то есть каждой его точке соответствует точка, получить которую можно поворотом на 180 градусов относительно начала координат. Поэтому графики таких функций можно строить в правой полуплоскости, а изображение в левой полуплоскости получить, повернув картинку на 180 градусов.

Верно и следующее: если функция задана графиком, который симметричен относительно начала координат, то она нечетная.

3. Определить, является ли четной функция: .

Область определения может быть найдена из системы неравенств:

0> <>0>>><>” title=”delim >>0> <>0>>><>”/>

Таким образом, область определения симметрична, и не содержит выколотые точки (1) и (-1).

Подставляем (-х) вместо х:

– исходную функцию не получили, а получили совсем другую – значит, исходная функция не является ни четной, ни нечетной (что и подтверждает график). Мы убедились, что симметрия области определения еще не означает, что функция четная или же нечетная.

4. Определить, является ли четной функция: .

Область определения – вся числовая ось, кроме 0 – симметричная.

Подставляем (-х) вместо х:

– функция нечетна.

5. Определить, является ли четной функция: .

Область определения – вся числовая ось, кроме точек 3 и (-3) – симметричная.

Подставляем (-х) вместо х:

– функция четная.

6. Определить, является ли четной функция: .

Область определения – вся числовая ось – симметричная.

Подставляем (-х) вместо х:

– функция четная.

7. Определить, является ли четной функция: .

Область определения – вся числовая ось, кроме 0 – симметричная.

Подставляем (-х) вместо х:

– функция нечетная.

Кроме того, здесь мы имеем дело с суммой двух функций.

Сумма двух нечётных функций – нечётна.

Сумма двух чётных функций – чётна.

А вот сумма двух функций разной четности – как правило, ни четна, ни нечетна.

Определим четность этих функций по отдельности.

– функция нечетная.

– функция нечетная.

8. Исследуем теперь такую функцию:

Одна из них нечётна – это мы только что показали, а вторая?

Область определения функции симметрична, функция нечётна, так как . Тогда по правилу сложение двух нечетных функций даст функцию нечетную.

9. Наконец, последняя:

– имеем произведение двух функций.

Произведение или частное двух нечётных функций чётно.

Произведение или частное двух чётных функций чётно.

Произведение или частное нечётной и чётной функций нечётно.

Так как обе функции являются чётными, то и их произведение чётно.

Область определения – вся числовая ось. Производим подстановку:

– функция четная.

Общие сведения

Исследование функции на четность и нечетность — базовый элемент, показывающий ее поведение, которое зависит от значения аргумента. Последний является независимой переменной, соответствующей определенным допустимым значениям. Множество чисел, которое может принимать неизвестная независимого типа, называется областью определения. Областью значений функции вида y = f (x) являются все значения зависимой переменной «y».

Теперь следует сформулировать список базовых знаний, которые необходимы для анализа выражений на четность. Если нужно выполнить другие процедуры исследования, то его следует расширить. Например, для нахождения максимума следует ознакомиться с производной. Необходимый минимум знаний о функциях следующий:

Первый элемент необходим для выявления аргумента, при котором можно узнать его недопустимые значения, а также определить симметричность. От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.

Область определения

Первый элемент, который нужен для анализа, следует рассмотреть подробнее. Область определения функции z = g (y) специалисты рекомендуют обозначать литерой «D». Полная запись выглядит таким образом: D (z). Кроме того, следует выяснить симметричность множества. Под последним понимается некоторый интервал, который нужно найти.

D (z) записывается в виде множества. Например, D (z) = [1;8]. Запись значит ограниченность аргумента, принимающего значения от 1 включительно до 8 включительно, то есть следующие цифры: 1, 2, 3, 4, 5, 6, 7 и 8. Если указана запись в виде (1;4), то ее нужно трактовать таким образом: от 1 не включительно до 4 не включительно, то есть в интервал входят только числа 2 и 3.

Для определения величины D (z) необходимо решить неравенство, корнем которого являются все значения аргумента. Для этих целей можно использовать и специализированное программное обеспечение. Математики рекомендуют свести пользование решебниками и программами к минимуму, поскольку не всегда предоставится возможность воспользоваться ими на экзаменах или контрольных.

Основные виды

Исследование функции зависит от ее вида, который нужно правильно определять. Для начала следует обозначить сложность, поскольку от этого параметра зависят дальнейшие действия и свойства, которыми придется руководствоваться. Математики производят разделение таким образом:

Алгебраические делятся на рациональные (без корня) и иррациональные (наличие радикала). Первые состоят из целых и дробных. D (z) для этих типов — все множество действительных чисел. Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.

Все функции, содержащие sin, cos, tg и ctg, являются тригонометрическими. Кроме того, arcsin, arccos, arctg и arcctg — обратные тригонометрические. Трансцендентные можно разделить на такие три группы: показательные, степенные и логарифмические.

Второе отличается от первого формулой. Другой тип классификации основан на периодичности. В зависимость от этого параметра все функции делятся на периодические и непериодические. Параметр периодичности означает повторение ее поведения через определенный период Т.

Существует еще один критерий. Он называется монотонностью. В зависимости от него, функции бывают монотонными и немонотонными. Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.

Правила для выявления

Для того чтобы исследовать на четность, существует два правила или теоремы, которые записываются в виде двух формул. Четная — функция вида w (x), для которой справедливо такое равенство: w (-x) = w (x). Для нечетной соотношение немного другое: w (-x) = w (x). Однако бывают выражения, к которым не применимы эти тождества. Они принадлежат общему виду.

Для оптимизации решения специалисты рекомендуют использовать некоторую последовательность действий или специальный алгоритм. Он позволяет определить четность за минимальный промежуток времени и без ошибок. Необходимо обратить внимание на пункты или шаги, по которым выполняется подробная оценка:

Следствия из утверждений

Свойства или следствия из утверждений расчетов позволяют оптимизировать процесс решения, поскольку нет необходимости выполнять какие-либо действия. Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут. Математики выделяют следующие свойства для таких функций:

Второе свойство можно записать математически таким образом: z (x) = y (x) + w (x). Выражение y (x) можно выразить следующим образом: y (x) = [z (x) — z (-x)] /2. Тождество w (x) выражается через z (x) формулой: w (x) = [z (x) + z (-x)] /2.

Классификация по четности

Специалисты давно уже исследовали некоторые функции. Примеры четных и нечетных можно классифицировать по признаку четности. Эти данные значительно ускоряют процесс анализа любого выражения. К нечетным функциям относятся следующие (следует учитывать, что аргумент «x» принадлежит множеству действительных чисел Z):

Кроме того, существуют еще составные выражения, элементами которых являются простые функции. Для анализа необходимо руководствоваться свойствами. Следующий класс, который объединяет все четные выражения, состоит из следующего перечня:

Остальные составляют класс общего вида, который не принадлежит к четным и нечетным. При решении задач необходимо иметь таблицу всех функций, которая должна быть составлена перед обучением. Следует учитывать, что на экзаменах и контрольных функции, используемые для описания каких-либо процессов, практически не исследуются. Зная алгоритм, не составит особого труда проверить выражение на четность. Следующим этапом, который поможет закрепить теоретические знания, считается практика.

Пример решения

Задачи исследования функции на четность встречаются редко, поскольку этот элемент входит в полный анализ ее поведения. Пусть дано тождество z (y) = (y 2 — y — 2) / (y 2 — 1). В этом случае следует действовать по алгоритму:

Задачу можно решить вторым способом — проанализировать составляющие элементы. Например, знаменатель всегда будет нечетным, поскольку от четного y 2 отнимается нечетное число (6 — 1 = 5). Этот способ используется в некоторых языках программирования, для написания подпрограмм и процедур, позволяющих проверить или отобрать все нечетные значения. Числитель также является нечетным, поскольку он содержит нечетный элемент «y». Если построить график, используя любой из веб-ресурсов, то он окажется симметричным относительно начала координат.

Первое свойство свидетельствует о том, что функция является нечетной. Некоторые новички делают распространенную ошибку, считая, что отношение нечетных есть величина четная. Однако такое утверждение не применимо в этом случае. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.

Таким образом, для исследования функции на предмет ее четности или нечетности нужно воспользоваться специальным алгоритмом, который рекомендуют математики. Он позволит выполнить операцию без ошибок и за короткий промежуток времени.

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы дадим строгие определения четных и нечетных функций, рассмотрим их свойства и решим некоторые задачи. Важным свойством четной функции является симметричность графика функции относительно оси у, важным свойством нечетной функции является симметричность графика относительно точки начала координат. Также на уроке мы выработаем методику исследования функции на четность и нечетность и решим ряд задач.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Функции»

Тема урока, введение

В этом уроке будут даны строгие определения четных и нечетных функций, рассмотрены их свойства, решены некоторые задачи.

Основные определения

Определение 1: Функция

Определение 2: Функция

Дадим развернутое определение четной функции.

Определение 3: Функцию

1. Область определения симметрична относительно нуля, т.е.

2.

Из определения вытекает важное свойство четной функции:

График четной функции симметричен относительно оси y (Рис. 1).

Дадим развернутое определение нечетной функции.

Определение 4: Функцию

1. Область определения симметрична относительно нуля, т.е.

2.

Из определения нечетной функции вытекает свойство: График нечетной функции симметричен относительно т. (0; 0) (Рис. 2).

Если функция не является ни четной, ни нечетной, то ее называют функцией общего вида.

Примеры

Пример 1. Определите вид функции

четная функция, ее график симметричен относительно оси y.

Пример 2. Определите вид функции

В точке функция общего вида.

Пример 3.Определите вид функции

Обе точки выколотые, график и область определения симметричны относительно начала координат, функция четная.

Пример 4. Определите вид функции

рафик и область определения симметричны относительно начала координат, функция нечетная.

Пример 5. Определите вид функции

Пример 6. Определите вид функции

Область определения симметрична относительно нуля, функция нечетная.

Примеры на исследование функции

Рассмотрим примеры на свойства четных и нечетных функций.

Пример 7: Исследовать на четность функцию

,функция четная.

Возведем в квадрат обе части равенства. Тогда вместо уравнения получим систему:

Второе уравнение полученной системы – уравнение окружности с центром в т.(0; 0) радиусом 4. Но т.к. является верхняя полуокружность (Рис. 9).

График симметричен относительно оси y, поэтому функция четная.

Ответ: Функция четная.

Пример 8. Известно, что функция

Нам известно, что функция убывает на луче

График четной функции симметричен относительно оси y, т.е. функция возрастает на луче

В качестве примера изобразим график функции (Рис. 10).

Ответ: Функция возрастает при

Пример 9. Дана функция

Если функция четная, ее график симметричен относительно оси y, т.е. (Рис. 11).

Если функция нечетная, ее график симметричен относительно т. (0; 0), т.е. (Рис. 12).

Заключение, вывод

Мы рассмотрели определения и свойства четных и нечетных функций, решили некоторые типовые задачи На следующем уроке мы продолжим изучение свойств четных и нечетных функций.

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

Рекомендованные ссылки на интернет-ресурсы

1. Раздел College.ru по математике (Источник).

2. Интернет-проект «Задачи» (Источник).

3. Образовательный портал «РЕШУ ЕГЭ» (Источник).

Рекомендованное домашнее задание

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 275 – 278.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Источник