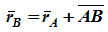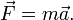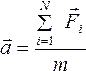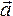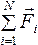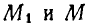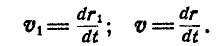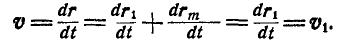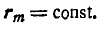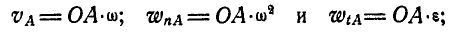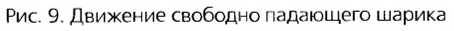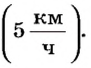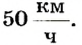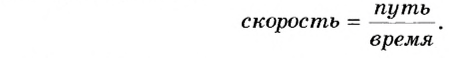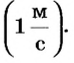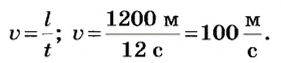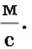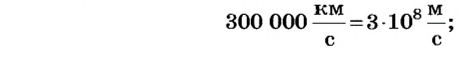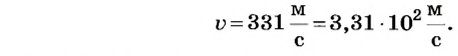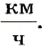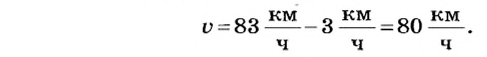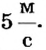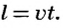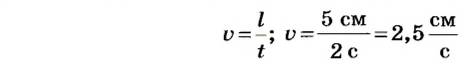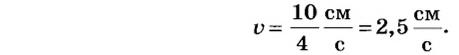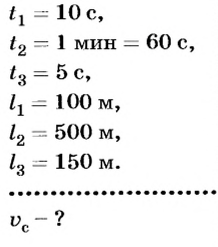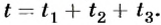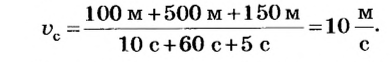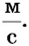Что относится к поступательному движению

Поступательное движение

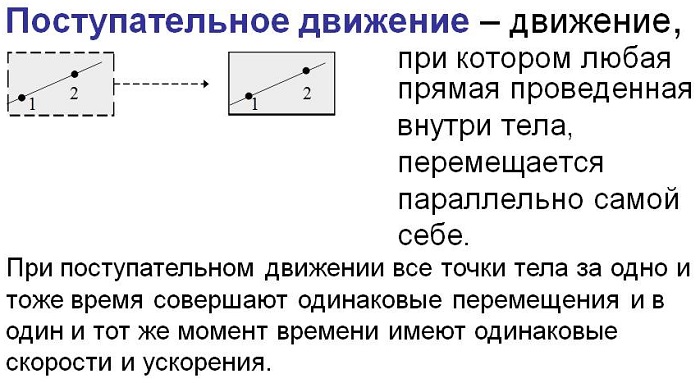
Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени. [1]

В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.

Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу.Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения (См. Рис. 2)

Содержание

Примеры поступательного движения

Поступательно движется, например, кабина лифта. Также, в первом приближении, поступательное движение совершает кабина колеса обозрения. Однако, строго говоря, движение кабины колеса обозрения нельзя считать поступательным.

В соответствие с первым и вторым законами Ньютона кабина, стремясь сохранить направление своего движения, отклоняется от вертикальной прямой, причём в разном направлении по разные стороны от оси симметрии колеса обозрения. Таким образом, не всякая прямая, связанная с кабиной, перемещается параллельно самой себе. Причём отклонение кабины от вертикальной прямой, и соответственно, отклонение траектории движения кабины от траектории поступательного движения тем больше, чем больше частота вращения колеса обозрения. Учитывая, что реальные частоты вращения колёс обозрения достаточно малы, траектории движения их кабин весьма близки к траектории поступательного движения. Этим можно объяснить, что во многих источниках движение кабины приводится в качестве примера поступательного движения.

Моделью поступательного движения в первом приближении (если пренебречь качанием ступни) является педаль велосипеда, совершающая при этом за полный цикл своего хода один поворот вокруг своей оси.

Связь движения тела и движения его точек

Если тело движется поступательно, то для описания его движения достаточно описать движение произвольной его точки (например, движение центра масс тела).

Одной из важнейших характеристик движения точки является её траектория, в общем случае представляющая собой пространственную кривую, которую можно представить в виде сопряжённых дуг различного радиуса, исходящего каждый из своего центра, положение которого может меняться во времени. В пределе и прямая может рассматриваться как дуга, радиус которой равен бесконечности.

В таком случае оказывается, что при поступательном движении в каждый заданный момент времени любая точка тела совершает поворот вокруг своего мгновенного центра поворота, причём длина радиуса в данный момент одинакова для всех точек тела. Одинаковы по величине и направлению и векторы скорости точек тела, а также испытываемые ими ускорения.

При решении задач теоретической механики бывает удобно рассматривать движение тела как сложение движения центра масс тела и вращательного движения самого тела вокруг центра масс (это обстоятельство принято во внимание при формулировке теоремы Кёнига).

Источник

Поступательное движение в школьной программе изучает предмет физика. Для понимания, что оно собой представляет, каким законам подчиняется, изучим основную терминологию и рассмотрим понятие на конкретных примерах, которые встречаются в повседневной жизни.

Что такое поступательное движение

Перемещение твердого тела (всех взаимосвязанных его точек) с помощью механического воздействия по заданной траектории и в определенном направлении, в результате которого отрезок из двух любых точек данного тела будет всегда параллелен своему расположению, предшествующему нынешнему, в каждый отрезок времени, называется поступательным движением.

В процессе перемещения характеристика объекта не меняется: по составу, форме и величинам сторон. Причем в любой отрезок времени точки объекта обладают одним и тем же направлением модулей векторов скорости и ускорения, а их величины равны.

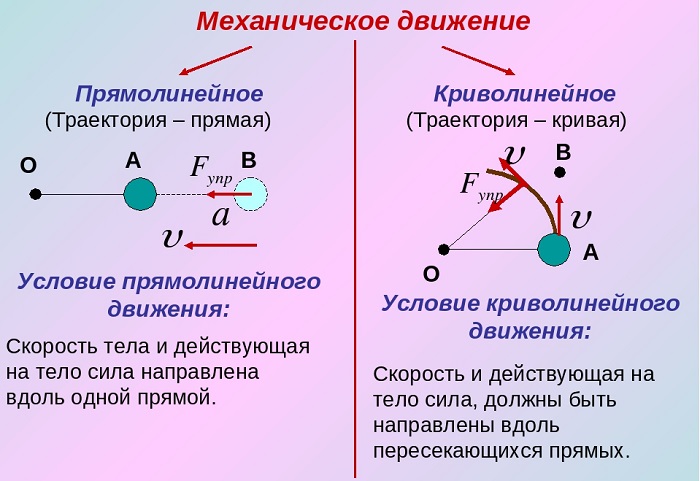
Выделяют прямолинейное поступательное движение и криволинейное.

В качестве примеров поступательного движения в можно привести функционирование по определенной траектории различного оборудования и механизмов.

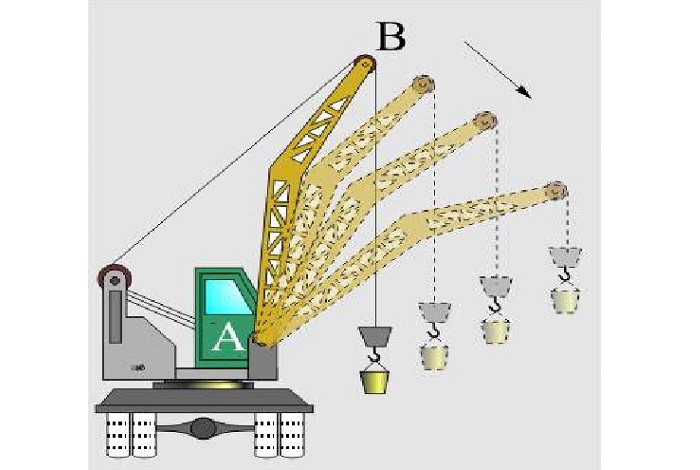
перемещение стрелы с грузом строительного подъемного крана относительно его кабины, в которой сидит рабочий;

подъем и спуск лифта в шахте;

педали у велосипеда. При этом каждая его точка, напротив, совершает вращательные движения;

совершение кабиной оборотов на колесе обозрения в парках аттракционов.

Теорема о поступательном движении

Материальные точки объекта (тела), осуществляющего поступательные движения, перемещаются по одному и тому же пути, а скорости и ускорения в каждый промежуток времени совпадают по модулю вектора и направлению.

Доказательство теоремы

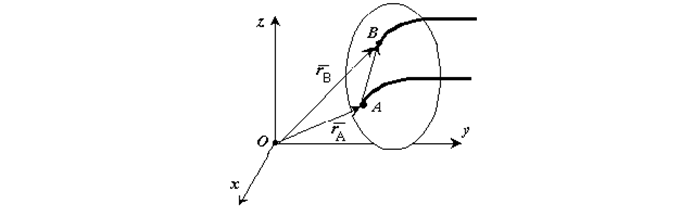
Докажем данную теорему. Для этого необходимо провести прямую линию через две любые точки твердого тела, осуществляющего поступательное движение – пусть это будут точки А и В.

Полученный отрезок АВ совершает перемещение по заданному пути: А описывает траекторию АА₁А₂А₃А_n, а В соответственно – В₁В₂В₃В_n.

Отсюда следует, что:

Принимая во внимание, что размеры данного отрезка АВ неизменны (const) при перемещении, а сам он имеет свойство двигаться в пространстве параллельно своему предыдущему местоположению, значит направления точки А и точки В совпадают.

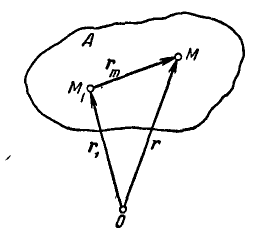
Соотношение радиусов-векторов точек А и В в системе координат относительно ее начала – О (Рис 1),

можно выразить формулой:

где линии пути точки А соответствует функция r_A(t), точки B – r_B(t).

Теорема доказывает, что для определения поступательного движения твердого материального объекта достаточно знать параметры перемещения любой одной его точки. Следовательно, изучая кинематику передвижения точки тела, решается задача определения поступательного движения.

Основной закон динамики поступательного движения

Основной закон динамики поступательного движения трактует II закон Ньютона.

Формулировка закона звучит следующим образом:

Совокупность равнодействующих сил, оказывающих воздействие на материальное тело, способствует возникновению ускорения. То есть, ускорение прямо пропорционально векторному суммарному значению оказываемых на него сил, и обратно пропорционально массе объекта.

Основное уравнение закона приведено ниже:

Причем у равнопеременного движения векторное ускорение

II закон Ньютона работает исключительно в ИСО (инерциальная система отсчета), где объекты двигаются равномерно, прямолинейно или находятся в состоянии покоя.

Источник

Поступательное движение твердого тела в теоретической механике

Содержание:

Поступательное движение твердого тела:

До сих пор мы изучали движения одной материальной точки. Перейдем теперь к изучению движения твердого тела. Начнем с изучения простого вида движения тела—поступательного, а затем рассмотрим более сложные виды его движений.

Движение тела называется поступательным, если любая прямая, неизменно связанная с телом, перемещается параллельно самой себе. Примерами поступательного движения тела могут служить движение кузова вагона на прямолинейном участке пути, движение поршня внутри цилиндра и пр.

Пусть тело А (рис. 160) движется поступательно.

Возьмем две любые точки твердого тела

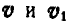
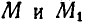
Выразим скорости точек по формуле (72):

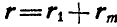
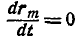
Но так как , то

в силу того, что

Отсюда следует, что при поступательном движении тела все его точки описывают конгруэнтные кривые, имеют равные скорости, а следовательно, и равные ускорения.

Поэтому, изучение поступательного движения тела может быть сведено к изучению движения одной его какой-либо точки. Следовательно, все выводы, полученные при исследовании движения одной точки, могут быть распространены на случай поступательного движения тела.

Задача:

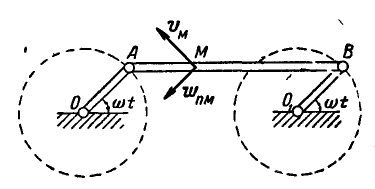
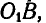
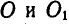
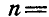
Клавиша соломотряса АВ соединена шарнирно в точках А и В с одинаковыми кривошипами OA и делающими вокруг осей постоянное число оборотов 240 об/мин (рис. 161).

Определить скорость и ускорение любой точки М клавиши, если .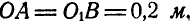

Решение. При равенстве длин кривошипов и одинаковом числе их оборотов клавиша АВ движется поступательно, а поэтому точка М движется тождественно с точками А и В. Скорость и ускорение точки А находим по формулам (89) и (91):

но так как по формуле (94):

Скорость и ускорение точки М, равные скорости и ускорению точки А, показаны на рисунке 161.

Поступательное движение твердого тела

Поступательным движением называют такое движение твердого тела, при котором любая прямая, взятая в теле, остается параллельной своему начальному направлению

Поступательное движение тела и его уравнение

Наиболее простым движением твердого тела является поступательное движение. Соединим две какие-либо точки тела отрезком прямой. При поступательном движении тела этот прямолинейный отрезок передвигается параллельно самому себе, не изменяя своего направления. Движение тела называют поступательным, если каждая проведенная в теле прямая сохраняет свое направление.

Из определения видно, что поступательное движение может совершать только тело. Одна точка не может двигаться поступательно. Вместе с тем поступательное движение твердого тела вполне характеризуется движением любой из его точек.

Если тело движется поступательно, то все его точки описывают одинаковые траектории.

Пусть некоторое тело совершает поступательное движение относительно системы координат хОуz (рис. 97, а), которую мы примем за неподвижную и будем называть основной системой отсчета. Отметим в этом теле какую-либо точку Е, движущуюся вместе с телом. Не обращая пока внимания на прочие точки тела, рассмотрим движение точки Е, которое, как движение всякой точки, определяется уравнениями

Давая аргументу t последовательные значения, получим положения точки Е, геометрическое место которых является ее траекторией. На рис. 97 траектория не изображена.

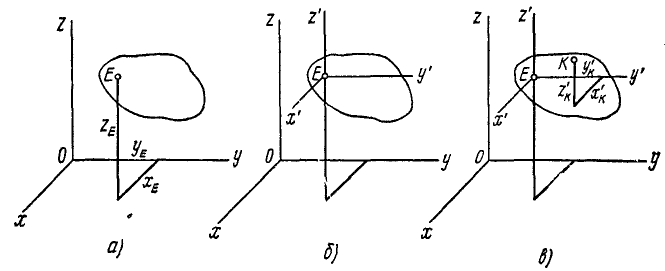
Рис. 97

Проведем теперь в теле через E три взаимно перпендикулярные оси (рис. 97, б), которые назовем подвижной системой отсчета, или подвижными осями координат. Для простоты доказательства в этом параграфе подвижные оси взяты параллельными неподвижным. Подвижные оси передвигаются вместе с телом относительно основных осей, оставаясь им параллельными, по условию поступательного движения.
Отметим в теле какую-либо другую точку К (рис. 97, в), координаты которой относительно подвижных осей обозначим x’κ, y’κ и z’, а относительно основных:

Обратим внимание на то, что координаты x’_K, y’_K и z’_K точки К относительно подвижных осей постоянны, потому что и точка К и подвижные оси взяты в одном и том же твердом теле. Следовательно, при всяком положении поступательно движущегося тела координаты точек E и K отличаются друг от друга на постоянные величины. Отсюда следует, что траектории точек E и К одинаковы и одинаково ориентированы относительно основной системы координат xОyz. Поскольку точки выбраны нами произвольно, доказанное относится к любым точкам тела.

Если определять движение тела по движению его точек, то можно определить поступательное движение тела как движение, при котором перемещения всех точек тела за один и тот же произвольно выбранный промежуток времени равны между собой.

Именно поэтому поступательное движение иногда различают по траекториям, описываемым точками тела. Так, например, говорят, что спарник паровой машины, установленной на фундаменте, совершает круговое поступательное движение; это означает, что все точки спарника описывают одинаковые окружности. Говорят, например, что поршень совершает прямолинейное поступательное движение; это означает, что все точки поршня описывают одинаковые и параллельные прямолинейные траектории.

Задача:

Определить движение спарника тепловоза на прямолинейном участке пути.

Решение. Спарник AB (рис. 98) — это стержень, соединенный шарнирами А и В с кривошипами OA и O1B равной длины. Длина спарника равна расстоянию между осями О и O₁. Такой механизм O₁OAB называют шарнирным параллелограммом. Противоположные звенья его, как противоположные стороны всякого параллелограмма, параллельны между собой: AB ∣∣ OO₁.

При заданном движении тепловоза точки О и O₁ движутся прямолинейно и прямая AB не меняет своего направления, т. е. движется поступательно. (При повороте тепловоза или при изменении уклона железнодорожного пути поступательное движение нарушается.) Все точки спарника описывают одинаковые траектории — укороченные циклоиды.

Ответ. Движение спарника AB поступательное.

Задача:

Круг l радиуса r₁ (рис. 99, а) движется поступательно, постоянно соприкасаясь с неподвижным кругом ll радиуса r₂. Найти траекторию любой точки круга l.

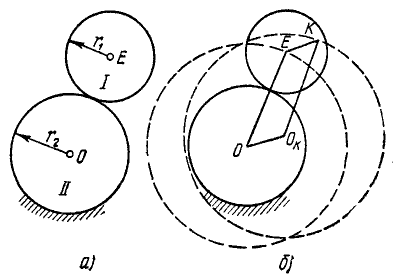
Рис. 99

Решение. Возьмем на подвижном круге l произвольную точку К и соединим с ней центр E подвижного круга отрезком EK (рис. 99, б). От центра О неподвижного круга ll отложим отрезок При поступательном движении круга l отрезок EK, как всякая прямая, проведенная в поступательно движущемся теле, не меняет своего направления и остается равным и параллельным неподвижному отрезку OO_K. Соединив точку О с точкой Е, а точку О_K — с точкой К, получим параллелограмм KE00_K, в котором

Следовательно, при поступательном движении круга l по кругу ll точка К движется, оставаясь на постоянном расстоянии r₁ + r₂ от неподвижной точки О_K, т. е. описывает окружность.

Ответ. Точки круга l описывают окружности радиуса r₁ + r₂.

Задать движение тела — это значит дать положение всех его точек для каждого мгновения. Мы видим, что при поступательном движении твердого тела все его точки движутся одинаково и движение всего тела вполне характеризуется движением какой-либо из его точек. Следовательно, уравнения движения точки E являются одновременно и уравнениями поступательного движения тела.

Часто даже в тех случаях, когда движущееся тело не является твердым, пренебрегают движением некоторых его частей по отношению к другим частям и рассматривают движение системы как по ступательное движение абсолютно твердого тела. Например, движение поезда иногда принимают за поступательное, пренебрегая вращением колес, движениями частей машины и т. п.

Если тело движется поступательно, то все его точки имеют одинаковые скорости

Скорости точек поступательно движущегося тела

Чтобы определить проекции скорости произвольной точки К поступательно движущегося тела на неподвижные оси координат, продифференцируем по времени уравнения (79), помня, что xκ, ук и z’κ постоянны. Найдем

Отсюда следует, что равны и полные скорости (64), и направляющие косинусы (62), иными словами, что равны векторы скоростей точек E и К:
(80 / )

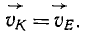
Поскольку эти точки взяты произвольно, доказанное относится к любым точкам тела, а потому во всякое мгновение скорости всех точек поступательно движущегося тела одинаковы.

Одинаковость скоростей не следует понимать как их постоянство, как неизменяемость во времени. Если тело движется поступательно, то в данное мгновение скорости всех точек тела одинаковы; с течением же времени скорости могут измениться. Но если изменится скорость одной точки, то на столько же изменятся скорости всех других точек тела, и они опять-таки останутся одинаковыми.

Одинаковость скоростей всех точек тела — необходимый, но недостаточный признак поступательного движения тела.

Может оказаться, что в какое-либо мгновение скорости всех точек тела одинаковы, но в следующее мгновение они различны. Так, например, движение шатуна AB кривошипно-ползунного механизма не является поступательным, но при некоторых положениях механизма (рис. 100) скорости всех его точек одинаковы.

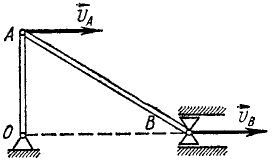
Рис. 100

Если тело движется поступательно, то все его точки имеют одинаковые ускорения

Ускорения точек поступательно движущегося тела

Продифференцировав по времени (80), найдем

откуда следует, что равны векторы ускорений обеих точек:

(81′)

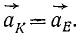
Траектории точек K и E одинаковы и одинаково расположены, а потому к написанным равенствам надо присоединить еще следующие:
a_KT = a_ET и a_KN=a_EN

Во всякое мгновение ускорения всех точек поступательно движущегося тела одинаковы. В этой теореме, как и в предыдущей, одинаковость не надо понимать как неизменяемость с течением времени.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Поступательное движение

В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.

Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу. Однако, рассматриваемое как физический процесс, оно представляет собой в трёхмерном пространстве вариант винтового движения (см. Рис. 2).

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Простейшие механизмы — устройства, служащие для преобразования направления и величины (модуля) силы. Представляют собой элементы более сложных механизмов. Некоторые из простейших механизмов появились в глубокой древности.

В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу; это энергия движения и сопровождающего его взаимодействия.

В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).

Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.

Источник

Содержание:

Поступательное движение:

В природе, технике, быту существует много видов механического движения тел. Простейшим из них является поступательное движение.

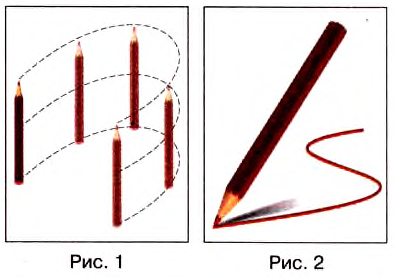
Движение автомобиля на прямолинейном участке дороги, движение поршня в цилиндре двигателя автомобиля, движение ящика, который мы выдвигаем из стола — это примеры поступательного движения. Во время поступательного движения любое выделенное направление в движущемся теле, например планка в выдвижном ящике, остаётся параллельным своему исходному положению. На рисунке 1 показано поступательное движение карандаша — видим, что в разные моменты движения карандаши параллельны.

Если непрерывно фиксировать в пространстве положения определённой материальной точки подвижного тела, то получим линию, которую называют траекторией движения.

Когда материальная точка движется вдоль прямой, то такое движение называют прямолинейным, а если траектория точки кривая, — криволинейным.

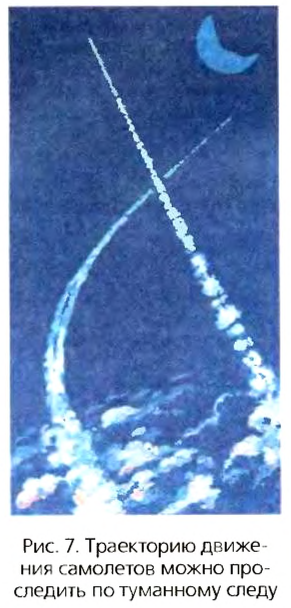
Часто траекторию тела можно наблюдать наглядно — карандаш во время письма оставляет след на бумаге—траекторию движения кончика грифеля (рис. 2). Траекторию полёта самолёта определяем по его следу в небе (рис. 3).

Форма траектории зависит от выбора тела отсчёта. Например, относительно Земли траектория движения Луны является окружностью, а относительно Солнца — линией сложной формы.

В дальнейшем, если не указаны другие тела отсчёта, будем рассматривать движение тел относительно Земли.

Когда тело движется по своей траектории, то длина её пройденного участка со временем увеличивается.

Длину траектории, которую тело описывает во время движения за определённый интервал времени, называют путём.

Путь обозначают малой латинской буквой 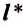. Единицей пути в СИ является один метр (1 м).

В научной и учебной литературе путь ещё обозначают малой латинской буквой s.

На практике пользуются также другими единицами пути:

Механическое движение и время

Механическое движение нельзя рассматривать, не указывая время движения. На этом примере 8 видно единство пространства и времени.

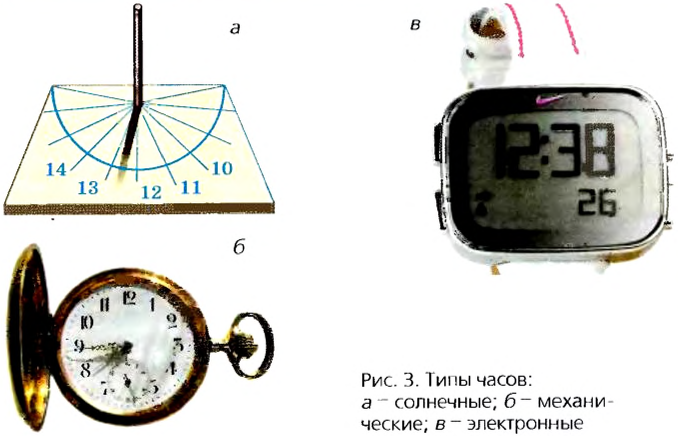
Время, как и другие физические величины, можно измерить. Измеряют время при помощи часов, которые условно можно разделить на естественные и искусственные. Часы отражают единство времени и движения, так как в каждом таком приборе (часах) используется тот или иной вид движения.

В основу естественных (природных) часов положены движения Солнца, Луны, Земли. Давно замечено, что эти небесные тела регулярно повторяют свое положение относительно других тел. Так, Солнце ежедневно у нас восходит в восточной части небосвода, а заходит в западной. Это является следствием вращения Земли вокруг своей оси. Время одного оборота Земли вокруг своей оси назвали сутками. Время между двумя восходами Солнца, следующими один за другим, равно одним суткам.

Механические и электронные часы значительно точнее, поэтому широко используются в науке, технике, быту. Для особо точных измерений применяют атомные часы, в которых используются явления, происходящие в атомах и молекулах. При помощи таких часов определили, что одни сутки отличаются от других на тысячные доли секунды.

Как единицы времени используют сутки, год, час, минуту, секунду. Основной1 единицей времени является секунда. Единицы времени соотносятся между собой так:

Физическое тело и материальная точка

Все тела, окружающие нас, в физике называют физическими телами. Тела состоят из какого-либо вещества, имеют определенный объем и форму. Они могут считаться движущимися или неподвижными в зависимости от выбора тела отсчета. При этом может двигаться как тело в целом, так и отдельные его части.

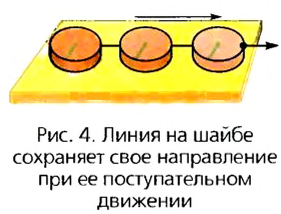
Движение физического тела, при котором любая линия, нанесенная на теле, остается параллельной своему предыдущему положению, называют поступательным.

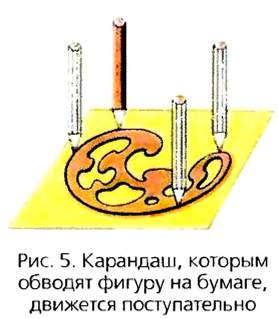
Поступательно движется кузов автомобиля на горизонтальной прямой дороге, груз, поднимаемый краном, карандаш, при помощи которого рисуют сложную фигуру на бумаге (рис. 5).

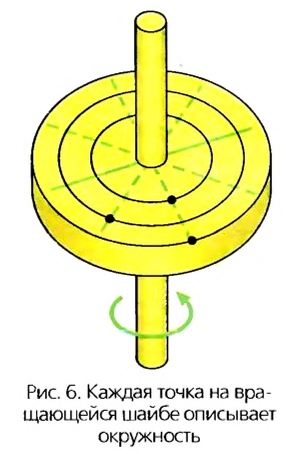
Закрепим шайбу на металлической оси так, чтобы она проходила через центр шайбы, и начнем ее вращать (рис.6). Линия на шайбе все время изменяет свою ориентацию в пространстве, каждая ее точка описывает окружность.

Движение физического тела, когда каждая его точка движется по окружности называют вращательным.

Для упрощения изучения закономерностей механического движения в физике иногда применяют искусственный прием, когда возможно пренебречь формой и размерами тел.

Если размерами и формой тела пренебрегают, то его считают материальной точкой.

Поезд, движущийся от Киева до Львова, расстояние между которыми около 600 км, можно считать материальной точкой, поскольку его длина значительно меньше проходимого расстояния. Но этот же поезд, стоящий на вокзале, не может считаться материальной точкой для пассажира, которому необходимо преодолеть расстояние от локомотива до последнего вагона.

Траектория движения тела

В механическом движении тело, которое можно считать материальной точкой, постепенно переходит из одной точки пространства в другую. Совокупность таких точек образует непрерывную линию.

Линию, описанную телом во время механического движения, называют траекторией его движения.

Для исследования механических движений тел используют различные явления, которые делают траектории их движения видимыми. Так, при полете самолета на большой высоте переохлажденный пар воды конденсируется на частичках сгорания топлива и образуется туманный след, хорошо видимый на фоне голубого неба (рис.7).

О траектории движения можно судить по следам лыжника на снегу, по следам колес лунохода на поверхности Луны.

Для исследования движений используют различные виды фотографирования, создание специальных документальных киноматериалов. На рисунке 8 изображены следы движения микрочастиц, из которых состоят атомы и молекулы. По этим следам определяют свойства микрочастиц и их поведение в различных условиях.

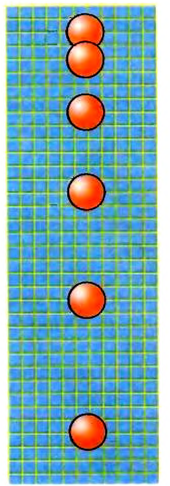
По виду траектории движения делятся на прямолинейные и криволинейные. Выпущенный из руки мячик падает на землю по прямой линии. Это видно на фотографии (рис. 9), где зафиксированы положения мячика через одинаковые интервалы времени. Такие фотографии называются стробоскопическими, или стробограммами.

Если траектория движения тела прямая линия, то такое движение называют прямолинейным.

Мячик, брошенный под углом к горизонту, имеет криволинейную траекторию (рис. 10).

Если траектория движения тела кривая линия, то движение называют криволинейным.

Следует всегда иметь в виду, что вид траектории движения тела зависит от выбора тела отсчета. Велосипедисту, сидящему в седле и вращающему педали, кажется, что все точки колес движутся по окружностям. Для наблюдателя, стоящего у дороги, траектории движения этих точек кажутся более сложными (рис. 11).

Если бы астронавт наблюдал Солнечную систему, находясь далеко за ее пределами, то он бы заметил, что планеты движутся но вытянутым окружностям (эллипсам). Находясь на Земле, астрономы наблюдают движение планет по очень сложным траекториям. Форма траектории зависит от выбора тела отсчета.

Траектория относительна, ее вид зависит от выбора тела отсчета.

Удачный выбор тела отсчета позволяет значительно упростить решение ряда задач механики, если при этом траектория движения тел упрощается. Ученые древности считали, что звезды и планеты движутся вокруг Земли как центра Вселенной. В этом случае траектории движения планет были очень сложными и практически невозможно было предусмотреть, как они будут двигаться в будущем. Когда польский ученый Миколай Коперник (1473-1548) установил, что все планеты Солнечной системы, как и Земля, вращаются вокруг Солнца, то расчеты их движений стали значительно проще.

Путь, который проходит тело

Тело в своем движении переходит из одной точки пространства в другую. Длина описанной телом траектории все время увеличивается. Зная начальное положение тела, вид траектории и ее длину, можно определить положение тела в любой момент времени.

Длину траектории, описанной телом за определенное время (интервал времени), называют пройденным телом путем.

В любом движении тел пройденный ими путь только увеличивается. Так, если вы от парты к доске преодолели 5 м пути и вернулись на место по той же траектории, то пройденный вами путь будет равен 10 м.

Путь как физическая величина не имеет направления, но имеет численное значение в определенных единицах, равное длине траектории. В математических записях путь обозначают малой буквой .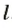

Для измерения пути используют приборы, как и для измерения линейных размеров тел: линейки, рулетки, измерительные ленты и т. п. (рис. 12). В автомобилях, велосипедах, мотоциклах используют счетчики оборотов колес, которые сразу показывают длину пройденного пути. На рисунке 13 изображен велосипедный счетчик.

Основной единицей длины является метр (м). Используются также кратные и дольные единицы длины: километр (км), дециметр (дм), сантиметр (см), миллиметр (мм) и др.

В астрономии используют такие единицы длины:

Допускается также использование таких единиц, как морская миля (1 миля = 1852 м) и ангстрем (1 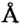= 10 10 м).

Скорость движения тела

В своем движении тело за определенное время проходит определенный путь. Человек пешком за два часа проходит до 10 км, а автомобиль за такое же время проедет 100 км. Сравнивая движения человека и автомобиля, говорят, что автомобиль движется быстрее человека.

Для сравнения движения различных тел в физике используют такую характеристику движения, как скорость.

Пешеход в рассмотренном выше примере за 1 ч проходит 5 км.

Таким образом, его скорость равна 5 километрам в час

Соответственно автомобиль в рассмотренном примере имеет скорость

Для вычисления скорости механического движения тела необходимо пройденный им путь разделить на время, за которое этот путь пройден:

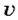
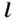
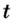
Если обозначить скорость , путь , а время , то получим формулу для определения скорости:

Основной единицей скорости есть метр в секунду

Пример №1

С какой скоростью летел самолет, если за 12 с он преодолел путь 1200 м?

Дано:

Решение

Ответ. Самолет летел со скоростью 100

Скорость тела в каждый момент времени или в каждой точке траектории движения называется мгновенной скоростью. Мгновенная скорость имеет направление и определяется приборами, которые называются спидометрами.

Приводим примеры некоторых скоростей:

Могут использоваться кратные и дольные единицы скорости:

В морском деле иногда используют единицу скорости узел: 1 узел = 1 миля/ч = 0,514 м/ч.

Исследуем движение пассажира в вагоне движущегося поезда, идущего в направлении локомотива. Пусть расчеты показывают, что относительно вагона он движется со скоростью 3 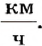Расчеты наблюдателя, неподвижного относительно полотна дороги, показывают, что пассажир движется со скоростью 83

Отсюда можно сделать вывод, что поезд движется со скоростью

Относительность движения ввел в рассмотрение выдающийся ученый Г. Галилей.

Числовое значение скорости не дает полной информации о движении тела. Важно также знать, в каком направлении движется тело. Поэтому часто скорость на рисунках и схемах изображают при помощи стрелок, показывающих направление движения тела. Длина же стрелки в определенном масштабе показывает значение скорости.

Пример №2

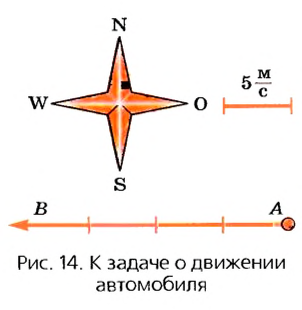
Автомобиль движется с востока на запад со скоростью 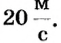Изобразить эту скорость графически (рис. 14).с

Выполним задание в несколько этапов.

1. Покажем на бумаге направление восток—запад. Обозначим движущееся тело точкой А и от нее проведем луч восток—запад.

2. Выбираем масштаб: 1 см на бумаге отвечает скорости

3. Отложим на луче 4 отрезка по 1 см и поставим в конце отрезка стрелку в направлении движения точки А. Отрезок АВ отвечает значению скорости 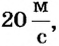а стрелка показывает направление движения.

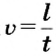
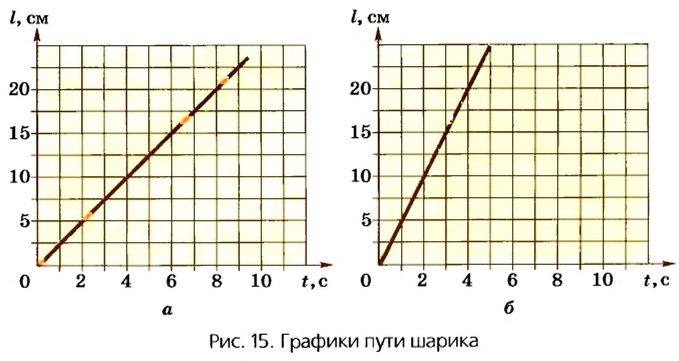
В физике и технике приходится определять пройденный телом путь, если известны скорость и время его движения. Для этого из формулы для определения скорости находят путь:

На графике такая зависимость изображается прямой линией. На рисунке 15, а показана зависимость пути от времени при движении стального шарика в вязкой жидкости. По графику можно определить, что через каждые 2 с путь шарика увеличивался на 5 см, т. е. скорость движения шарика

В этом случае скорость движения шарика не изменяется со временем. Движение, скорость которого не изменяется со временем, называют равномерным. При равномерном движении тело за любые одинаковые интервалы времени проходит одинаковые отрезки пути.

Движение равномерно, когда скорость постоянна.

На рисунке 15,6 показан график пути шарика, когда за каждые 2 с он проходит путь 10 см. Скорость шарика в этом случае

По наклону графика пути можно судить о скорости движения тела или сравнивать скорости разных тел: чем больше скорость, тем круче график пути.

Зная пройденный телом путь и скорость его движения, легко найти время его движения:

Средняя скорость

Наблюдая движения различных тел, можно отметить, что большинство из них не движутся равномерно. Так, скорость автомобиля вначале увеличивается, затем определенное время может оставаться постоянной, а при остановке уменьшается.

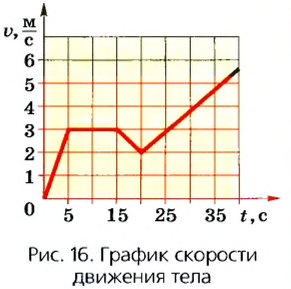
На рисунке 16 изображен график скорости движения тела. Из графика видно, что за первые 5с скорость увеличивалась от 0 до 3

Движение тела с изменяющейся скоростью называют неравномерным.

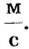
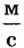
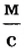
Следующие 10 с тело двигалось равномерно со скоростью 3 Между 15-й и 20-й секундами скорость уменьшилась с 3 до 2 . После этого скорость снова начала возрастать.

Такие подробности в описании движения не всегда нужны. Так, нас не интересует скорость движения автобуса на отдельных участках пути, а только время прибытия автобуса в необходимый пункт. Поэтому часто пренебрегают изменениями скорости движения, а учитывают только пройденный путь и время его прохождения. Рассчитанную в таком случае скорость называют средней.

Среднюю скорость 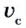определяют по формуле:

Средней скоростью называют физическую величину, характеризующую неравномерное движение и равную отношению пути, пройденного телом, к интервалу времени его прохождения.

Зная среднюю скорость движения тела, можно рассчитать путь, проходимый телом, и время его движения:

Пользуясь понятием средней скорости, расчеты для неравномерного движения выполняют так же, как и для равномерного движения.

Средняя скорость показывает, с какой скоростью должно было двигаться тело равномерно, чтобы данный путь преодолеть за такое же время, как и при неравномерном движении.

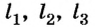
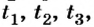
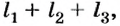
Среднюю скорость нельзя понимать как среднее арифметическое значение скоростей. Поэтому если отдельные участки пути тело проходило за соответствующие интервалы времени то для вычисления средней скорости необходимо сначала найти весь пройденный путь разделить на все время движения:

Пример №3

Легковой автомобиль за 10 с от начала движения прошел путь 100 м, затем за 1 мин — 500 м, а еще за 5 с — 150 м. С какой средней скоростью двигался автомобиль?

Дано:

Решение

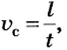
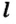
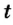
По определению средняя скорость где — пройденный телом путь, — время движения тела на этом пути.

Общий путь 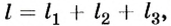а общее время движения

Ответ. Средняя скорость движения автомобиля 10

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник