Что открыли арабы в математике
Математики исламского средневековья
Математика Востока, в отличие от древнегреческой математики, всегда носила более практичный характер. Соответственно наибольшее значение имели вычислительные и измерительные аспекты. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия, механика, оптика. Начиная с эллинистической эпохи, в странах Востока огромным уважением пользовалась персональная астрология, благодаря этому суеверию поддерживалась также и репутация астрономии и математики.
Доступная нам история математики в странах Ближнего и Среднего Востока начинается в эпоху, следующую за эпохой мусульманского завоевания (VII—VIII века). Первая стадия этой истории состояла в переводе на арабский язык, изучении и комментировании трудов греческих и индийских авторов. Размах этой деятельности впечатляет — список арабских переводчиков и комментаторов одного только Евклида содержит более сотни имён. Арабский язык долгое время оставался общим языком науки для всего исламского мира. С XIII века появляются научные труды и переводы на персидском языке.
Культурной столицей исламского мира первоначально был Багдад, где халифы создают «Дом мудрости», в который приглашаются виднейшие учёные всего исламского мира — сабии (потомки вавилонских жрецов-звездопоклонников, традиционно сведущие в астрономии), тюрки и др.
В целом, эпоха исламской цивилизации в математических науках может быть охарактеризована не как эпоха поиска новых знаний, но — как эпоха передачи и улучшения знаний, полученных от греческих математиков. Типичные сочинения авторов этой эпохи, дошедшие до нас в большом количестве — это комментарии к трудам предшествеников и учебные курсы по арифметике, алгебре, сферической тригонометрии и астрономии. Некоторые математики стран ислама виртуозно владели классическими методами Архимеда и Аполлония, но новых результатов получено немного.
Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, поставила перед математикой и сама религия ислама. Это задача о расчёте лунного календаря, об определении точного времени для совершения намаза, а также об определении киблы — точного направления на Мекку.
Числовая система
Арабская нумерация вначале была буквенной и, видимо, она финикийско-еврейского происхождения. Но с VIII века багдадская школа предложила индийскую позиционную систему, которая и прижилась.
Дроби в арабской математике, в отличие от теоретической арифметики древних греков, считались такими же числами, как и натуральные числа. Записывали их вертикально, как индийцы; черта дроби появилась около 1200 года. Наряду с привычными дробями в быту традиционно использовали разложение на египетские аликвотные дроби (вида 1/n), а в астрономии — 60-ричные вавилонские. Попытки ввести десятичные дроби делались, начиная с X века (ал-Уклидиси), однако дело продвигалось медленно. Только в XV веке ал-Каши изложил их полную теорию, после чего они получили некоторое распространение в Турции. В Европе первый набросок арифметики десятичных дробей появился раньше (XIV век, Иммануил Бонфис из Тараскона), но победоносное их шествие началось в 1585 году (Симон Стевин).
Понятия отрицательного числа в исламской математике в целом выработано не было. Некоторым исключением стала книга «Мухаммедов трактат по арифметике» ал-Кушчи (XV век). Ал-Кушчи мог познакомиться с этой идеей, будучи в молодости послом Улугбека в Китае. Перевод этой книги на латинский впервые в Европе содержал термины positivus и negativus (положительный и отрицательный).
Математики исламского средневековья
В IX веке жил Ал-Хорезми — сын зороастрийского жреца, прозванный за это ал-Маджуси (маг). Заведовал библиотекой «Дома мудрости», изучал индийские и греческие знания. Ал-Хорезми написал книгу «Об индийском счёте», способствовавший популяризации позиционной системы во всём Халифате, вплоть до Испании. В XII веке эта книга переводится на латинский, от имени её автора происходит наше слово «алгоритм» (впервые в близком смысле использовано Лейбницем). Другое сочинение ал-Хорезми, «Краткая книга об исчислении аль-джабра и аль-мукабалы», оказало большое влияние на европейскую науку и породило ещё один современный термин «алгебра». В книге разбираются линейные и квадратные уравнения. Отрицательные корни игнорируются. Алгебры в нашем смысле тоже нет, всё разбирается на конкретных примерах, сформулированных словесно. Новые математические результаты в книгах ал-Хорезми фактически отсутствуют.
В развитии инфинитизимальных методов существенного продвижения не было. Сабит Ибн Курра вывел другим способом несколько результатов Архимеда, а также исследовал тела, полученные вращением сегмента параболы (купола). Ибн ал-Хайсам дополнил его результаты.
В средневековой исламской математике было сделано довольно много попыток доказать Пятый постулат Евклида. Чаще всего исследовалась фигура, позднее названная четырёхугольником Ламберта. Ал-Джаухари, Сабит ибн Курра, Омар Хайям и другие математики дали несколько ошибочных доказательств, явно или неявно используя один из многочисленных эквивалентов V постулата.
Одним из величайших учёных-энциклопедистов исламского мира был Ал-Бируни. Он родился в Кяте, столице Хорезма. В 1017 году афганский султан Махмуд захватил Хорезм и переселил Ал-Бируни в свою столицу, Газни. Несколько лет Ал-Бируни провёл в Индии. Главный труд Ал-Бируни — «Канон Мас‘уда», включающий в себя множество научных достижений разных народов, в том числе целый курс тригонометрии (книга III). В дополнение к таблицам синусов Птолемея (приведенных в уточнённом виде, с шагом 15′), Ал-Бируни даёт таблицы тангенса и котангенса (с шагом 1°), секанса и пр. Здесь же даются правила линейного и даже квадратичного интерполирования. Книга Ал-Бируни содержит приближённое вычисление стороны правильного вписанного девятиугольника, хорды дуги в 1°, числа π и др.
Прославленный поэт и математик Омар Хайям (XI—XII вв.) внёс вклад в математику своим сочинением «О доказательствах задач алгебры и аль-мукабалы», где изложил оригинальные методы решения кубических уравнений. До Хайяма был уже известен геометрический метод, восходящий к Менехму и развитый Архимедом: неизвестное строилось как точка пересечения двух подходящих конических сечений. Хайям привёл обоснование этого метода, классификацию типов уравнений, алгоритм выбора типа конического сечения, оценку числа положительных корней и их величины. К сожалению, Хайям не заметил возможности для кубического уравнения иметь три вещественных корня. До формул Кардано Хайяму дойти не удалось, но он высказал надежду, что явное решение будет найдено в будущем. В «Комментариях к трудностям во введениях книги Евклида» (ок. 1077), Хайям рассматривает иррациональные числа как вполне законные. В этой же книге Хайям пытается решить проблему пятого постулата, заменив его на более очевидный.
Насир ад-Дин ат-Туси, выдающийся персидский математик и астроном, наибольших успехов достиг в области сферической тригонометрии. В его «Трактате о полном четырехстороннике» (1260) тригонометрия впервые была представлена как самостоятельная наука. Трактат содержит довольно полное и целостное построение всей тригонометрической системы, а также способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси. Сочинение ат-Туси стало широко известно в Европе и существенно повлияло на развитие тригонометрии. Ему принадлежит также первое известное нам описание извлечения корня любой степени; оно опирается на правило разложения бинома.
Джемшид Ибн Масуд ал-Каши, сотрудник школы Улугбека, написал сочинение «Ключ арифметики» (1427). Здесь вводится система десятичной арифметики, включающая учение о десятичных дробях, которыми ал-Каши постоянно пользовался. Он распространил геометрические методы Хайяма на решение уравнений 4-й степени. «Трактат об окружности» (1424) ал-Каши является блестящим образцом выполнения приближенных вычислений. Используя правильные вписанный и описанный многоугольники с числом сторон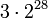 
(для вычисления стороны проводятся последовательные извлечения квадратных корней), аль-Каши для числа π получил значение 3,14159265358979325 (ошибочна только последняя, 17-я цифра мантиссы). В другой своей работе он сосчитал, что sin 1° = 0,017452406437283571 (все знаки верны — это примерно в два раза точнее, чем у ал-Бируни). Итерационные методы ал-Каши позволяли быстро численно решить многие кубические уравнения. Составленные ал-Каши самаркандские астрономические таблицы давали значения синусов от 0 до 45° через 1′ с точностью до девяти десятичных знаков. В Европе такая точность была получена только полтора столетия спустя.
Математика арабоязычного мира
Математика арабоязычного мира
На обширных территориях, от северо-запада Индийского полуострова до северного побережья Африки и юга Испании, существовали многочисленные восточные государства. Созданные нередко путем завоеваний, огромные, но не связанные в единый хозяйственный организм, они не обладали политической устойчивостью и имели сложную, полную превратностей судьбу. Научные и культурные традиции населяющих их народов развивались в таких условиях сравнительно медленно.
Начиная с VII века эти страны выделились из Византийской (Ромейской) империи под знаком борьбы за господство новой религии – ислама (или иначе магометанства, мусульманства). В течение ряда веков образовалась колоссальная область торгового обмена и экономических связей. Возникли большие города как центры торговли, ремесел и административного управления. Новая религия заняла господствующее положение, и арабский язык стал практически единым языком официальных документов, религиозных книг, научных трактатов и художественно-поэтических сочинений.
Условия хозяйственной и политической жизни благоприятствовали развитию математики, которая требовалась для государственного управления, ирригации, строительства, торговли и ремесел. Международные связи, осуществляемые с помощью длительных путешествий по морям, горам и неизведанным местностям, вынуждали развивать математику для нужд географии и астрономии.
Поэтому многие восточные правители и целые династии проводили политику государственного покровительства наукам. В аппарате государственного управления появились специально оплачиваемые ученые. Для них строились обсерватории, собирались библиотеки из древних сочинений, которые разыскивались всюду и переводились на арабский язык, привлекали на службу византийцев.
В результате сложилась своеобразная система математических знаний. В нее влились и данные ранней византийской науки, то есть классические трактаты Евклида, Архимеда, Аполлония и других, но получили свое развитие и сведения из математики Индии, а также коренного населения стран Ближнего и Среднего Востока.
Освоение и переработка многочисленных источников, как и подготовка квалифицированных математиков, потребовали, разумеется, немалого времени. Поэтому для арабской математики (как мы ее иногда называем, несмотря на необоснованность этого термина, так как ее развивали ученые разных национальностей) характерна пестрота в постановке задач, в методах их решения и даже в символике. Она получила так много оригинальных черт, что сделалась качественно отличной от своих источников.
Рассмотрим характерные особенности математики средневекового Востока и достигнутый уровень математических наук, без разделения математики по отдельным странам ввиду специфичности предмета и неразработанности темы.
В вычислительной практике арабов равноправно действовали обе системы счисления: десятичная абсолютная и шестидесятеричная. Первая была воспринята из Индии и быстро получила широкое распространение. Позже посредством арифметического трактата Хорезми (IX век) «Об индийских числах», переведенного в XII веке на латинский язык, десятичная система стала известной в Европе.
В Западной Европе десятичные дроби были введены только около 1585 года фламандским математиком и инженером С. Стевином. Вообще применение многих приемов, отработанных арабами до Х века, как, например, приближенного извлечения корней, отмечено в Европе лишь с середины XVI века.
Преобладание вычислительной части математики оказало влияние на трактовку многих теоретических вопросов. Особенно интересен вопрос о понимании алгебраических иррациональностей, стремление к оперированию с которыми характерно для всей арабской математики. В сочинениях Хорезми уже встречаются операции над квадратичными иррациональностями; Аль-Кархи (XI век) ввел многие преобразования иррациональностей. Аль-Баки (ок. 1100), как и Аль-Кархи, комментировал десятую книгу «Начал» Евклида, поясняя ее теоремы числовыми примерами.
В силу такого подхода и частого применения вычислений иррациональностей грань между рациональными числами и иррациональностями начинает стираться. К представлению о числе как о собрании единиц прибавились представления об отношениях непрерывных величин. Была установлена адекватность геометрической несоизмеримости с арифметической иррациональностью. В математике вместо двух обособленных понятий – числа и отношения, возникла новая, более широкая концепция действительного положительного числа. Уже в XIII веке этот факт был констатирован с полной определенностью; Насирэддин (1201–1274) писал: «Каждое из отношений может быть названо числом, которое определяется единицей так же, как один из членов этого отношения определяется другим из этих членов».
Можно сказать, что идея создания единой концепции действительного числа путем объединения рациональных чисел и отношений, появившаяся у математиков Византии, получила на Ближнем Востоке известное завершение. В Европе же подобная идея не появлялась довольно долго. Только с XVI века бурное развитие вычислительных средств начало приводить ученых к ее осознанию, а с достаточной степенью общности она была высказана лишь И. Ньютоном в 70-х годах XVII века (опубликована в 1707) в его «Всеобщей арифметике»: «Под числом мы понимаем не столько множество единиц, сколько отвлеченное отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу. Число бывает трех видов: целое, дробное и иррациональное. Целое число есть то, что измеряется единицей; дробное – кратной долей единицы; иррациональное число несоизмеримо с единицей».
Великий поэт и математик Омар Хайям (ок. 1048 – ок. 1122) и Насир-ад-дин ад-Туси (1201–1274) явно указывали, что каждое отношение величин, все равно, соизмеримых или нет, может быть названо числом. Величие этих достижений становится особенно ясным, если заметить, что полное признание отрицательных чисел европейскими математиками было достигнуто очень нескоро. Например, Ф. Виет (1540–1603), которому алгебра многим обязана, избегал отрицательных чисел, а в Англии протесты против отрицательных чисел раздавались даже в XVIII веке.
В XI веке тюрки-сельджуки захватили большую часть Ирана и византийских владений в Малой Азии. На этих землях народы осваивали и развивали наследие всех предшественников, и византийцев и арабов. Омар Хайям писал стихи по-персидски, научные трактаты по-арабски, а в служебных делах пользовался тюркским языком. Потерпев неудачу в прямом поиске корней произвольного кубического уравнения, он открыл несколько способов приближенного вычисления этих корней, предлагая сделать это, используя хорошо знакомые кривые. Как только (в XVII веке) Рене Декарт добавил к ней вторую идею – описать любую кривую с помощью чисел, родилась аналитическая геометрия, в которой решение алгебраических уравнений слито воедино с теорией чисел и с наглядной геометрией.
Предчувствуя эту связь, Омар Хайям поставил много интересных вычислительных опытов. Он нашел приближенные способы деления окружности на 7 или 9 равных частей; составил подробные таблицы синусов и с большой точностью вычислил число «пи». Он догадался, что это число иррациональное, и даже не квадратичное – но доказать не смог. Не удались Хайяму и попытки доказать пятый постулат Евклида о параллельных прямых.
Влияние алгоритмически-вычислительной направленности арабской математики отразилось и на ее структуре. В ней сравнительно быстро, впервые в истории, выделилась в качестве самостоятельной математической науки алгебра. В этом факте нашло свое выражение слияние элементов алгебраического характера математики различных народов, например: геометрическая алгебра византийцев, группировка однотипных задач и попытка выработать для каждой группы единый алгоритм в Вавилоне, вычислительные задачи индийцев, приводившие к уравнениям 1-й и 2-й степени, и т. п.
В трудах математиков средневекового Востока эти алгебраические элементы были впервые выделены, собраны в новый специальный отдел математики, сформулирован предмет этого нового отдела науки и построена систематическая теория. В качестве примера такого подхода приведем высказывание Омара Хайяма:
«Алгебра есть научное искусство. Ее предмет – это абсолютное число и измеримые величины, являющиеся неизвестными, но отнесенные к какой-либо известной вещи так, что их можно определить; эта известная вещь есть количество или индивидуально определенное отношение, и к этой известной вещи приходят, анализируя условия задачи; в этом искусстве ищут соотношения, связывающие данные в задачах величины с неизвестной, которая вышеуказанным образом составляет предмет алгебры. Совершенство этого искусства состоит в знании математических методов, с помощью которых можно осуществить упомянутое определение как числовых, так и геометрических неизвестных… Алгебраические решения… производятся лишь с помощью уравнения, то есть приравниванием одних из этих степеней другим».
Европейские ученые начали знакомиться с алгеброй в начале XII века, а источником их сведений явилось сочинение «Китаб аль-Джебр валь-Мукабала» Мухаммеда бен-Муса ал-Хорезми, жившего в первой половине IX века. Название в переводе означает: книга об операциях джебр (или гебр, восстановление) и кабала (приведение). Первая из операций, имя которой послужило названием для алгебры и служит до сего времени, состоит в переносе членов уравнения из одной стороны в другую. Вторая есть операция приведения подобных членов уравнения. Решение уравнений рассматривается как самостоятельная наука.
Книга Хорезми пользовалась большой известностью. Термин алгебра укоренился в математике. Осталось в этой науке и имя автора (аль-Хорезми) в латинизированном виде: алгоритм. Вначале это слово обозначало фамилию, затем нумерацию по позиционной системе, а теперь – всякую систему вычислений, производимых по строго определенным правилам и заведомо приводящих к решению поставленной задачи. В ходе развития науки изменялось содержание понятий, вложенных в эти термины, но термины сохранились.
Но сам Хорезми никогда не высказывался о своем приоритете в алгебре. Видимо, оба приема – джебр и кабала – были уже широко распространены в его время.
Алгебраические арабские трактаты IX–XV веков, помимо решения уравнений 1-й и 2-й степени, включали в себя и кубические уравнения. К последним приводили разнообразные задачи:
а) рассечение шара плоскостью; б) трисекция угла; в) отыскание стороны правильного 9-угольника; г) отыскание стороны правильного 7-угольника и другие.
Одна из задач оптики: найти на данной окружности такую точку, чтобы луч, падающий из данной точки A, отразился в другую заданную точку В, приводила к уравнению 4-й степени.
В методах решения кубических уравнений отразилось многообразие средств, обычно присущее математике арабских ученых. Численные же решения уравнений развивались, начиная со способа проб (разработан Бируни, 972-1048) до изящного итерационного, быстро сходящегося, метода (Каши, ок. 1420).
Помимо выделения алгебры, важнейшей характерной чертой арабской математики было формирование тригонометрии. И в этой области происходил синтез разнообразных тригонометрических элементов: исчисление хорд и соответственные таблицы предшествующих ученых, в особенности результаты Птолемея и Менелая, операции с линиями синуса и косинуса у индийцев, накопленный опыт астрономических измерений.
Используя этот разнородный материал, математики стран Ближнего Востока и Средней Азии ввели все основные тригонометрические линии. В связи с задачами астрономии они составили таблицы тригонометрических функций с большой частотой и высокой точностью. Данных накопилось при этом так много, что стало возможным изучать свойства плоских и сферических треугольников, способы их решений. Получилась стройная система тригонометрии как плоской, так и сферической. Ее представляет, например, сочинение Насирэддина (1201–1274) «Трактат о полном четырехстороннике».
Арабское доказательство теоремы Пифагора
Тригонометрия в математике средневекового Востока приобрела положение отдельной математической науки. Из совокупности вспомогательных средств астрономии она преобразовалась в науку о тригонометрических функциях в плоских и сферических треугольниках и о способах решения этих треугольников. Алгоритмически-вычислительные средства стали играть в ней преобладающую роль. Оставался один только шаг: введение специфической символики, чтобы тригонометрия приобрела привычный нам аналитический облик. Однако для этого шага понадобилось много времени! Дальнейшее развитие эта наука получила со второй половины XVI века в Европе, в первую очередь под влиянием запросов мореплавания и астрономии. В конце этого века появилось и название науки – «тригонометрия», от греческого измерение треугольников.
В ряду геометрических сочинений обращают на себя внимание глубокие исследования по основаниям геометрии. В сочинениях Хайяма и Насирэддина мы находим попытки доказательства постулата о параллельных, основанные на введении эквивалентных этому постулату допущений. Имена этих математиков с полным правом могут быть помещены историками в длинном ряду предшественников неевклидовой геометрии.
Примерно в середине XV века развитие математических наук в описываемых нами здесь арабских регионах замедляется и прекращается. Причины этого явления лежат вне математики: они – в наступившем экономическом разобщении обширных территорий, о которых шла речь выше.
Данный текст является ознакомительным фрагментом.
Вклад арабов в науку
Математика
Основные научные достижения арабских ученых относятся ко времени Раннего Средневековья. Значителен был вклад арабов в математическую науку. В VIII в. – и особенно в IX-Х вв. – арабские ученые сделали важные открытия в области геометрии, тригонометрии. Живший в Х в. Абу-л-Вафа вывел теорему синусов сферической тригонометрии, вычислил таблицу синусов с интервалом в 15°, ввел отрезки, соответствующие секансу и косекансу. Поэт, ученый Омар Хайям написал «Алгебру» – выдающееся сочинение, в котором содержалось систематическое исследование уравнений третьей степени. Он также успешно занимался проблемой иррациональных и действительных чисел. Ему принадлежит философский трактат «О всеобщности бытия». В 1079 г. он ввел календарь, более точный, чем современный григорианский. В Багдадском халифате узнали о математических открытиях индийцев в VIII в. Сразу же подхваченная арабами цифровая система стала известна в Западной Европе под названием арабской к XII в. (через арабские владения в Испании).
Астрономия
Переведенный главный труд Клавдия Птолемея «Великое астрономическое построение», получивший по-арабски название «Ал-Маджисти» (переведенный с арабского на латинский язык под названием «Альмагест») стал для арабских ученых основой космологии, применявшейся на протяжении последующих 500 лет. В IX-Х вв. арабские ученые аль-Баттани и Абу аль-Вафа провели самые точные для того времени астрономические измерения, позволившие им составить астрономические таблицы.
Мухаммед ибн Ахмед аль-Бируни производил также точные астрономические измерения. Бируни наблюдал и описал изменение цвета Луны при лунных затмениях и явление солнечной короны при полных затмениях Солнца. Он высказал мысль о движении Земли вокруг Солнца и считал геоцентрическую теорию весьма уязвимой. Им было написано обширное сочинение об Индии и переведены на санскритский язык «Начала» Евклида и «Альмагест» Птолемея. Астрономические исследования средневековых арабских ученых вместе с другими достижениями арабской науки и техники становились позднее известными в Европе и стимулировали развитие европейской астрономии.
География
Большое практическое значение имели достижения арабов в области география. Арабские путешественники и географы расширили представления об Иране, Индии, Цейлоне и Средней Азии. С их помощью Европа впервые познакомилась с Китаем, Индонезией и другими странами Индокитая. Известные работы географов-путешественников:
— «Книга путей и государств» Ибн Хордадбека, IX в.
— «Дорогие ценности» – географическая энциклопедия Ибн Руста (начало Х в.)
— «Записка» Ахмеда Ибн Фадлана с описанием путешествия в Поволжье, Заволжье и Среднюю Азию
— 20 трактатов Масуди (X в.)
— «Книга путей и царств» Истахри
— 2 карты мира Абу-Абдаллаха аль-Идриса
— многотомный «Словарь стран» аль-Кинди Якута
— «Путешествие» Ибн Баттуты.
Примечательно, что Ибн Баттута за 25 лет своих путешествий прошел по суше и морю около 130 тысяч км. Он посетил все мусульманские владения в Европе, Азии и Византии, Северную и Восточную Африку, Переднюю и Среднюю Азию, Индию, Цейлон и Китай, обошел берега Индийского океана. Он пересек Черное море и от Южного берега Крыма проехал к низовьям Волги и устью Камы.
Уже упоминавшийся нами Бируни производил географические измерения. Он определил угол наклона эклиптики к экватору и установил его вековые изменения. Для 1020 г. его измерения дали значение 23°34’0″. Современные вычисления дают для 1020 г. значение 23°34’45». Во время путешествия в Индию Бируни разработал метод определения радиуса Земли. По его измерениям, радиус Земли оказался равным 1081,66 фарсаха, т. е. около 6490 км. В измерениях участвовал Аль-Хорезми. При Аль-Мамуне была предпринята попытка замерить окружность Земли. С этой целью ученые измерили градус широты вблизи Красного моря, что составляет 56 арабских милей, или 113,0 км, отсюда длина окружности Земли равнялась 40680 км.
Физика
Выдающимся ученым Египта был Ибн-аль-Хайсам (965—1039), известный в Европе под именем Алхазена, математик и физик, автор знаменитых трудов по оптике. Алхазен развивает научное наследие древних, производя собственные эксперименты и конструируя для этого специальные приборы. Он разработал теорию зрения, описал анатомическое строение глаза и высказал предположение, что приемником изображения является хрусталик. Точка зрения Алхазена господствовала до XVII в., когда было выяснено, что изображение появляется на сетчатке. Отметим, что Алхазен был первым ученым, знавшим действие камеры-обскуры, которую он использовал как астрономический прибор для получения изображения Солнца и Луны. Алхазен рассматривал действие, плоских, сферических, цилиндрических и конических зеркал. Он поставил задачу определения положения отражающей точки цилиндрического зеркала по данным положениям источника света и глаза.
Математически задача Алхазена формулируется так: по данным двум внешним точкам и окружности, расположенным в одной плоскости определить такую точку окружности, чтобы прямые, соединяющие ее с заданными точками, образовывали равные углы с радиусом, проведенным к искомой точке. Задача сводится к уравнению четвертой степени. Алхазен решил ее геометрически.
Алхазен занимался исследованием преломления света. Он разработал метод измерения углов преломления и показал экспериментально, что угол преломления не пропорционален углу падения. Хотя Алхазен не нашел точной формулировки закона преломления, он существенно дополнил результаты Птолемея, показав, что падающий и преломленный лучи лежат в одной плоскости с перпендикуляром, восстановленным из точки падения луча. Алхазену было известно увеличивающее действие плоско-выпуклой линзы, понятие угла зрения, его зависимость от расстояния до предмета. По продолжительности сумерек он определил высоту атмосферы, считая ее однородной. В этих предположениях результат получается неточным (до Алхазену, высота атмосферы 52 000 шагов), но сам принцип определения является большим достижением средневековой оптики. «Книга оптики» Алхазена была переведена на латинский язык в XII в. То, что Алхазен есть не кто иной, как арабский ученый Ибн аль-Хайсам, выяснилось только в XIX в.
Замечательны практические указания, приведенные Бируни о воде, применяемой при определениях плотности. Он указывает на необходимость пользоваться водой из одного и того же источника, в одних и тех же условиях «в связи с воздействием на ее свойства четырех времен года и зависимостью ее от состояния воздуха». Таким образом, Бируни знал, что плотность воды зависит от содержания в ней примесей и от температуры.
При сравнении с современными данными результаты Бируни оказываются весьма точными. Русский консул в Америке Н.Ханыков в 1857 г. нашел рукопись аль-Хазини под названием «Книга о весах мудрости». В этой книге приведены извлечения из книги Бируни «Об отношениях между металлами и драгоценными камнями в объеме», содержащие описание прибора Бируни и полученные им результаты. Аль-Хазини продолжал исследования, начатые Бируни, с помощью специально сконструированных им весов, которые он назвал «весами мудрости».
Медицина
Больших успехов достигла медицина – она развивалась более успешно, чем в Европе или на Дальнем Востоке. Арабскую средневековую медицину прославил врач и философ, Ибн-Сина – Авиценна (981-1037), автор энциклопедии теоретической и клинической медицины, обобщивший взгляды и опыт греческих, римских, индийских и среднеазиатских врачей «Канон врачебной науки», которая на Западе использовалась в качестве учебника до XVII века.
Авиценна родился в 980 году, а умер в 1037 году. Начав с профессии финансового инспектора в налоговом управлении, он пришел к должности визиря.
Абу Бакр Мухаммед ар-Рази, известный багдадский хирург, дал классическое описание оспы и кори, применял оспопрививание. Сирийская семья Бахтишо дала семь поколений знаменитых врачей.
В 975 г. персидский ученый Абу Мансур аль-Харави Мувффат опубликовал «Трактат об основах фармакологии», в котором изложил лечебные свойства различных природных и химических веществ.
Какие изобретения подарили миру мусульмане (20 фото)
22 октября 2014 13:27
СМОТРЕТЬ ВСЕ ФОТО В ГАЛЕРЕЕ
Согласно одной легенде, араб Халид (Khalid) пас своих овец в Каффе, регионе южной Эфиопии, и заметил, что животные становятся энергичнее, когда едят определенные ягоды. Собрав их, Халид сварил первый кофе.
Первые сведения о вывозе зерен касались экспорта кофе из Эфиопии в Йемен. Уже в 15 веке его завезли в Мекку и Турцию, откуда кофе попал в Венецию в 1645 году. В Англию зерна привез турок Паскуа Роси (Pasqua Rosee) в 1650 году, и открыл первую кофейню на лондонской улице Ломбард. Путь слова “кофе” весьма длинный: арабское “qahwa” превратилось в турецкое “kahve”. Итальянцы переняли его как “caff?”, у англичан появилось слово “coffee”, а у русских — “кофе”.
Древние греки считали, что глаза испускают свет и видят люди благодаря этому. О том, что на самом деле свет проникает в глаза, догадался Ибн аль-Хайтам (Ibn al-Haitham), мусульманский математик, астроном и физик, живший в 10 веке. Наблюдая за тем, как свет проникает сквозь щели ставней, он заметил, что чем меньше была щель, то тем лучше была видна картинка, и изобрел первую камеру-обскуру (“qamara” в переводе с арабского означает “темная или отдельная комната”). Также считается, что аль-Хайтам первым перевел физику из разряда философской науки в экспериментальную.
В шахматы играли еще древние индийцы, но игра значительно отличалась от той, которую мы знаем сегодня. Современный вариант шахмат появился в Персии, откуда и распространился на запад в Европу: в 10 веке в Испании игра была введена маврами.
За тысячу лет до братьев Райт, идея создать летательный аппарат пришла в голову мусульманскому поэту, астроному и инженеру Аббасу ибн Фирнасу (Abbas ibn Firnas). В 852 году он спрыгнул с крыши мечети в свободно развевающемся плаще с прикрепленными к нему деревянными дощечками. Фирнас надеялся, что будет парить как птица, но у него не получилось. Плащ замедлил падение, и стал чем-то вроде первого парашюта, и ученый отделался легким испугом и незначительными ушибами. В возрасте 70 лет, усовершенствовав свой аппарат, Фирнас повторил свою попытку, спрыгнув с горы. Ему удалось продержаться в воздухе 10 минут, но в итоге он разбился при приземлении: дело в том, что к своему аппарату он не приделал хвост.
Ежедневное купание – одно из требований ислама. Возможно, именно поэтому мусульмане занимались улучшением рецепта мыла. Известно, что подобие мыла было и у древних египтян, и у римлян, но именно арабы догадались смешать растительные масла с гидроксидом натрия и ароматическими соединениями. В Англии шампунь появился в 1759 году, когда некий мусульманин открыл баню в Брайтоне.
Ябир ибн Хайян (Jabir ibn Hayyan) – ученый, превративший алхимию в химию. В 9 веке он открыл процессы, которые до сих пор используются в современной науке: дистилляция, кристаллизация, плавление, рафинация, окисление, выпаривание и фильтрация. Хайян открыл серную и азотную кислоты, и изобрел перегонный аппарат, благодаря которому в мире появились алкогольные напитки и ароматы, используемые в производстве духов.
Коленчатый вал, устройство, превращающее ротационное движение в линейное, изобрел мусульманский инженер аль-Джазари (al-Jazari). Одно из самых важных изобретений механики, до сих пор являющееся одной из основных составляющих частей современных машин, первоначально использовалось в ирригации. Из книги инженера ясно, что он изобрел либо усовершенствовал вентили и клапаны, разработал первые механические часы. Аль-Джазари можно считать отцом робототехники. Замок с кодом – тоже его изобретение.
Стрельчатая арка – характерная черта европейских готических соборов, но идея таких арок была позаимствована из мусульманской архитектуры. Она была крепче полукруглой арки, используемой римлянами и норманнами, и, соответственно, позволяла строить более высокие и сложные зданий. Также европейцы переняли у мусульман идеи конструкции ребристых сводов и круглых окон-розеток. Европейские замки стали копией мусульманских с их бойницами, парапетами, барбаканами и квадратными башнями. Например, архитектором замка Генриха V был мусульманин.
Многие современные хирургические инструменты, включая скальпели, медицинские пилы, щипцы, тонкие ножницы, остались такими, какими их придумал мусульманский хирург аль-Захрави (al-Zahrawi). Именно он обнаружил, что кетгут, используемый для наложения внутренних швов, рассасывается в организме естественным путем и может быть применен при производстве медицинских капсул. В 13 веке, за 300 лет до Уильяма Гарвея (William Harvey), мусульманский врач Ибн Нафис (Ibn Nafis) описал процесс кровообращения. Мусульманские врачи изобрели анестетики и полую иглу для экстракции катаракты.
Ветряную мельницу арабы изобрели в 634 году и использовали для перемалывания кукурузы и снабжения водой. В арабских пустынях единственным источником энергии был ветер, месяцами дующий в одном направлении, и этот источник использовали на полную мощность. У мельниц было 6 или 12 крыльев, покрытых тканью и пальмовыми листьями. В Европе первые ветряные мельницы появились только через 500 лет.
Первыми идею прививки предложили не Дженнер и Пастер, а мусульмане. В Европу эта техника пришла из Турции в 1724 году, где в Стамбуле на эту процедуру обратила внимание жена английского посла. В Турции детям делали прививку от оспы за 50 лет до того, как вакцинацию открыли европейцы.
Первую авторучку придумали для султана в 953 году: правитель потребовал ручку, которая не пачкала бы его одежду и руки. Тогда система подачи чернил к кончику ручки была такой же, как сейчас.
Вероятно, система нумерации, которую используют во всем мире, происходит из Индии, но форма чисел – арабская, и впервые появилась в печатном виде в работе мусульманских математиков аль-Хваризми (al-Khwarizmi) и аль-Кинди (al-Kindi) в 825 году. Прототипом слова “алгебра” стало название книги аль-Хваризми “Al-Jabr wa-al-Muqabilah”, причем принципы, описанные в ней, до сих пор используются. Результаты работы мусульманских математиков, включая алгоритмы и некоторые теории тригонометрии, попали в Европу только через 300 лет. Открытый аль-Кинди частотный анализ послужил основанием для развития современной криптографии.
Концепцию обеда из трех блюд – супа, после которого едят мясо или рыбу, за которыми следуют фрукты и орехи – принес в 9 веке с собой из Ирака в Кордову Али ибн Нафи (Ali ibn Nafi). Он также ввел в обиход хрустальные стаканы (изобретенные, кстати, уже вышеупомянутым Аббасом ибн Фирнасом).
Ковры у средневековых мусульман считались неотъемлемой частью рая. Техника ткачества была довольно развита, постоянно появлялись новые краски, да и само искусство ткачей было не на последнем месте. В Европе же полы покрывали плетеными половиками, под которыми, вследствие плохой уборки, была куча мусора, кости, и не только. Неудивительно, что арабские и персидские ковры быстро прижились.
Если бы не мусульмане, чеков у нас не было бы. Само слово “чек” произошло от арабского “saqq”, которое означает письменное обязательство оплатить товар при доставке. Необходимость в чеках возникла из-за того, что перевозить деньги на большие расстояния было весьма опасно. Уже в 9 веке мусульманские бизнесмены могли обналичить чеки, выписанные на багдадские банки, в Китае.
В 9 веке уже многие мусульманские ученые считали, что Земля имеет форму шара. По словам астронома Ибн Хазма (Ibn Hazm), доказательством служил тот факт, что “Солнце всегда находится вертикально к определенной точке на Земле”. Это было за 500 лет до того, как об этом догадался Галилей. Вычисления мусульманских астрономов были настолько точны, что они ошиблись меньше чем на 200 километров при определении длины экватора, предположив, что она составляет 40253,4 километра.
В средневековой Европе были огороды, но именно арабы рассматривали сад как место для отдыха и медитации. Первые королевские сады такого рода появились в 11 веке в мусульманской Испании. Родина гвоздик и тюльпанов – тоже мусульманские страны.
10 изобретений мусульман, изменивших нашу жизнь
В связи с кризисом мигрантов в Европе и возрастающей террористической угрозой по миру прокатилась волна исламофобии. В докладе британской правозащитной организации Tell MAMA отмечается, что в 2015 году количество преступлений на почве ненависти к мусульманам увеличилось на 326 процентов. А недавние исследования ученых из Лейпцигского университета свидетельствуют, что каждый второй из 2420 опрошенных жителей Германии чувствует себя в своей стране некомфортно из-за множества мусульман. Радикальные противники ислама, в том числе россияне, высказывают мысль о том, что мир, возможно, был бы лучше без мусульман. Разного рода реплики на этот счет можно встретить и в СМИ, и в соцсетях. «Практика» разобрался, что потеряло бы человечество, если бы мусульман, и правда, никогда бы не было.
УНИВЕРСИТЕТЫ
Основательницей первого высшего учебного заведения в 859 году была мусульманская принцесса Фатима аль-Фихри. Как и многие другие образовательные учреждения исламского мира, марокканский университет Аль-Карауин находился на территории мечети. Благодаря покровительству султанов, он все время расширялся, здесь для мужчин и женщин преподавали не только богословие, но и медицину, математику, химию, историю, географию и прочие дисциплины.
Многие научные центры того времени также были организованы мусульманами: один из самых известных из них — Дом Мудрости — построен в 920-х годах.
МЕДИЦИНА
Безусловно, эта отрасль могла развиваться и без вклада в нее мусульман, но сложно предугадать, на какой стадии развития она бы сейчас находилась. Дело в том, что именно в Арабском халифате еще в 707 году появилась первая больница (сейчас ее бы назвали «бюджетная», поскольку финансировалась она государством). Здесь же придумали госпитали с медсестрами, начали функционировать медицинские институты. В течение многих веков именно мусульманские врачи считались экспертами в области исследования и лечения глазных болезней.
Известнейшего средневекового врача Авиценну на самом деле звали Ибн Сине. Он первым обратил внимание на то, что некоторые болезни могут быть заразными, описал проказу, открыл анестезию. Его труд «Канон врачебной науки» был настольной книгой медиков того времени, в ней, в том числе, описывались лекарственные средства, способы их изготовления и употребления. Этот учебник вплоть до XVIII века использовался в ведущих европейских медицинских институтах.
Именно мусульманские врачи провели хирургическую операцию по онкологии и придумали технологию, избавляющую от катаракты, которая используется до сих пор. Кроме того, арабский врач Абуль-Касим аз-Захрави изобрел множество сложных хирургические инструментов вроде скальпеля, шприцов и щипцов и описал их применение в операциях.
МЫЛО И ПАРФЮМЕРИЯ
Исламская религия предписывает человеку заботиться как о внутренней, так и о внешней чистоте. И уже в X веке в ванных комнатах в домах мусульман было многое из средств гигиены, которыми человек пользуется и сегодня — например, мыло. Конечно, оно существовало еще в античные времена в Египте и Римской империи, но именно арабы придумали его рецепт, использующийся до сих пор — смесь растительных масел, едкой щелочи и ароматизаторов. Кроме того, и шампунь пришел Европу именно благодаря мусульманам. А арабский ученый аль-Кинди еще в IX веке описал более ста методов и рецептов для создания духов.
ФОТОКАМЕРА
Арабский ученый Альхазен (Ибн аль-Хайсам) в X веке совершил революцию в оптике, поставив под сомнение утверждения Платона и Евклида о том, что свет — это лучи, которые испускаются глазом для «ощупывания» предметов. Свою теорию о том, что зрение — это результат восприятия глазом отраженного от предмета света — он доказывал не при помощи философии, а экспериментально.
Ученый использовал камеру-обскуру: в специальной палатке с небольшим отверстием в пологе навеса. На противоположной стороне, согласно принципу прямолинейности распространения света, лучи создавали перевернутое изображение. Например, такой способ позволял наблюдать за солнечным затмением без вреда для зрения.
ПЕРЬЕВАЯ РУЧКА
Еще в 974 году по заказу четвертого фалифа Фатимидского халифата аль-Муизз Лидиниллаха было создано устройство для письма, которое не пачкало одежду и руки. Небольшой резервуар в ручке удерживал чернила. До наших дней не сохранилось ни одного такого устройства, зато остались исторические тексты, упоминающие об этой первой перьевой ручке.
КОФЕ
Несмотря на то, что родиной кофе считается Эфиопия, свою популярность он приобрел на Аравийском полуострове в XIX веке, откуда о нем в дальнейшем узнал весь мир. Арабы долгое время шли к приготовлению кофе через заваривание, затем стали добавлять молоко и различные пряности вроде имбиря и корицы. Лишь в 17 веке турецкий кофе пришел в Великобританию, в Венеции первая кофейня появилась в 1645 году, а в Германии напиток стал известен только в 1683 году.
КАРТА
Карты существовали еще 3500 лет назад, тогда они были изображены на глиняных табличках. С появлением бумаги на нее стали переносить изображения местности. В результате, в VIII веке в Багдаде появились первые карты и путеводители для путешественников.
ЧАСЫ, КОДОВЫЕ ЗАМКИ И РОБОТЫ
Механик Аль-Джазари известен как Да Винчи исламского мира — именно он был родоначальником кибернетики. Ученый самостоятельно соорудил множество механизмов, которые в начале XIII века считались прорывными технологиями.
Среди его изобретений были водяные часы и водоподъемные машины, фонтаны и клапанные насосы, кодовые замки и металлические двери. Кроме того, он придумал незамысловатую технологию, заставлявшую человеческие фигурки играть на музыкальных инструментах. Музыка извлекалась «роботами» под действием различных рычагов, которые управляли барабанами и цимбалами.
МАТЕМАТИКА
Считается, что система исчисления родом из Индии, но используемые нами сегодня цифры арабские. Их мусульманские математики использовали их уже в начале IX века. Математика исламского Средневековья считалась очень развитой. Немалую роль в этом сыграла религия: мусульманам требовались расчеты лунного календаря, чтобы правильно определять направление на Мекку и время для совершения намаза.
Даже само слово «алгебра» происходит от названия первой книги по этой дисциплине, которую написал крупный мусульманский математик аль-Хорезми. С его именем также связывают введение десятичной системы счета, дробей и основ тригонометрии.
ЛЕТАТЕЛЬНЫЙ АППАРАТ
Впервые аппарат, по конструкции напоминающий аэроплан, был построен в 880 году ученым Ибн Фирнанасом. В ходе испытаний устройства ему удалось достаточно долго парить в воздухе, правда, неудачное приземление привело к серьезной травме спины. Спустя шесть веков эта конструкция получила свое развитие в работах Леонардо Да Винчи.
Арабские изобретения и успехи в науках.
Мы привыкли считать западный мир «краеугольным камнем» научного прогресса. Аристотель, да Винчи, Эйнштейн… А арабы — это, в лучшем случае, астрономия, математика и спирт.
Национальной науки, как и национальной таблицы умножения, не существует. Если кто-то претендует на первенство в фундаментальных дисциплинах — значит, он ничего не знает о достижениях арабской науки. Ведь когда-то этот народ настолько опередил время, что, сложись история иначе, на Луне уже давно стоял бы зеленый флаг с полумесяцем.
Арабские изобретения и в то, в чем арабы весьма преуспели:
— цифры
— спирт
— астролябия (прибор для определение небесных светил на небе)
— ладан
— слово алгебра стало из известно Европе благодаря арабскому слову ал-джебр
— слово химия от арабского ал-кимийя
— названия многих географических объектов произошло от арабских слов, т.к. арабские купцы много путешествовали и торговали по миру, намного раньше чем европейцы имея представление о других континентах,странах, морях,океанах
— арабы научили европейцев пользоваться китайским компасом и порохом
— многие «морские» слова в наше время имеют так же арабское происхождение,например :адмирал, галера, баржа и т.д.
— мыло (7 век) известно арабам намного раньше,чем европейцам
— шампунь, европейцы научились изготавливать его лишь в 1903 году(
— духи и различные ароматические масла/благовония
— в 8 веке багдадские ученые получили керосин
— в 9 веке арабы чистили зубы веточками дерева арак, активный компонент которого входит в состав современных зубных паст.
— дистиллированная вода
— «царская водка» смесь кислот,которые растворяют даже благородные металлы
— щербет
— сироп
— ветряная мельница, вентилятор, переключатель, водяная и паровая турбина
— в медицине арабы изобрели порядка 200 инструментов, которые применяются до сих пор, а именно: скальпель, пинцет, хирургическую иглу, шприц с тонкой стеклянной иглой, пила для кости, гипсовая повязка и т.д.
— арабы первыми стали применять анестезию, кладя на лицо человека повязку, пропитанную опиантами
— при проведении операция антисептики были обязательны, кстати турки первыми начали вакцинацию от оспы.
— арабы применяли трахеотомию
— открытия нитроглицерина, азотной и серной кислот, калия, аммиачной соли
— 953 году по требованию халифа Египта была сконструирована первая в мире авторучка с встроенным резервуаром для чернил
— оптика