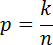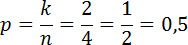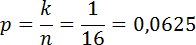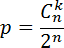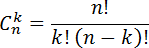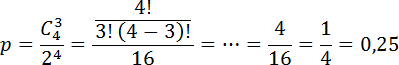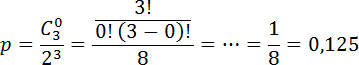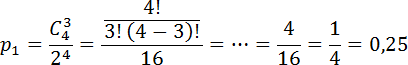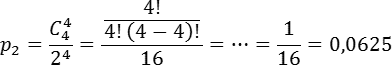Что орел что решка выпадет

Бросание монет. Решение задач на нахождение вероятности

Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать «бросают 3 монеты» или «бросают монету 3 раза», результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).

1. Классическое определение вероятности

Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Пример 2. Дважды бросают симметричную монету. Найти вероятность того, что оба раза выпала одна сторона.

Как видим, все довольно просто. Перейдем к чуть более сложной задаче.

Пример 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.

Взяли разгон и переходим к 4 монетам.

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Думаю, к этому времени вы уже поняли суть метода и сможете сами решить задачи, где бросаются 2-3-4 монеты и орел не выпадает ни разу, или решка ровно один раз и т.п.

2. Комбинаторика + классическая вероятность

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Конечно, этот подход кажется сложнее из-за более формального математического описания решения, но гораздо легче масштабируется.

Например, если рассмотреть подобную задачу:

Пример 5. Монету бросают 8 раз. Найти вероятность того, что герб выпадет ровно 4 раза

Ради полноты изложения приведу еще пример задачи, решаемой подобным образом (но если хотите, можете сразу переходить к более простому способу 3).

Пример 6. Монету подбрасывают 6 раз. Найти вероятность того, что гербы выпадут два раза и только подряд, а в остальные разы будут только решки.

Способ 3. Формула Бернулли

А теперь все задачи решаются проще простого, вот глядите!

Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Пример 7. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.

Пример 8. Пусть бросают 8 монет. Найти вероятность того, что орел не менее 7 раз.

Таким образом, используя одну простейшую формулу, можно решать множество задач, причем неважно, 3 монеты бросается, или 30, сложность расчетов примерно одинакова. Но, если число бросков становится очень большим, удобнее использовать приближенные формулы Муавра-Лапласа, о которых можно узнать здесь.

Полезные ссылки

Решебник по вероятности

А здесь вы найдете более 200 задач о бросании монет с полными решениями (вводите часть текста для поиска своей задачи):

Источник

Бросить монету

Быть или не быть, вот в чем вопрос.

Как делать правильный выбор каждый раз?

Вы когда-нибудь разрывались между двух вариантов не в состоянии принять решение? Верите, что простой бросок монеты может гарантировать, что Вы будете делать правильный выбор каждый раз?

Когда Вы взвесили все плюсы и минусы, выслушали все советы, рассмотрели вопрос со всех возможных сторон, и до сих пор мучительно в течение нескольких дней или недель, не можете прийти к решению, пришло время, чтобы бросить монету.

Сделайте один вариант орлом, а другой решкой. Подумайте об этом минуту, представьте два варианта на сторонах монеты. Сделайте глубокий вдох, и бросьте монету.

У Вас есть ответ. И он правильный.

Как понять решка или орел на монете?

По сути при броске монеты это не имеет большого значения, так как любую сторону монеты можно условно назвать орлом, а другая значит будет решкой. Главное определиться где что перед броском.

Важно это может быть для коллекционеров, у них существует целый ряд правил по которым определяется аверс (орел) и реверс (решка) монеты.

Примеры использования

Монета может использоваться как для игры в «Орел или Решка» (Орлянку), так и при необходимости принятия случайного решения из двух одинаково приемлемых вариантов (например, при жеребьёвке в различных видах спорта).

Так как вероятность выпадения одного из двух вариантов одинакова, этим способом пользуются, когда нужно принять решение. Например, перед началом футбольного матча судья подкидывает монетку и таким образом определяется, на какой половине поля начнёт игру та или иная команда.

Источник

Задачи B6 с монетами

Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:

где искомая вероятность, число устраивающих нас событий, общее число возможных событий.

Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа В этом и состоит вся сложность.

Тем не менее, существует как минимум два принципиально различных метода решения:

Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!

Метод перебора комбинаций

Этот метод еще называется «решение напролом». Состоит из трех шагов:

К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:

Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.

Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):

Итого варианта. Теперь выпишем те варианты, которые подходят по условию задачи:

Таких вариантов оказалось Находим вероятность:

Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем все возможные комбинации орлов и решек:

OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP

Всего получилось вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, Осталось найти вероятность:

Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.

Специальная формула вероятности

Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:

Теорема. Пусть монету бросают Тогда вероятность того, что орел выпадет ровно можно найти по формуле:

Где C_n k — число сочетаний которое считается по формуле:

Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.

На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.

Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.

По условию задачи, всего бросков было Требуемое число орлов: Подставляем в формулу:

С тем же успехом можно считать число решек: Ответ будет таким же.

Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем числа Поскольку монету бросают 3 раза, А поскольку решек быть не должно, Осталось подставить числа в формулу:

Напомню, что 0! = 1 по определению. Поэтому C ₃ 0 = 1.

Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.

Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.

Пусть вероятность того, что орел выпадет 3 раза. Тогда Имеем:

Теперь найдем вероятность того, что орел выпадет все 4 раза. В этом случае Имеем:

Чтобы получить ответ, осталось сложить вероятности p ₁ и p ₂. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:

p = p ₁ + p ₂ = 0,25 + 0,0625 = 0,3125

Источник

Что орел что решка выпадет

Задача 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Общее число равновозможных комбинаций может быть четыре:

«орел-орел», «орел-решка», «решка-орел», «решка-решка».

Из них благоприятных исходов по условию задачи два – это «орел-решка» и «решка-орел». Следовательно, искомая вероятность, равна

.

Задача 2. В случайном эксперименте симметричную монету бросают три раза. Найдите вероятность того, что решка выпадет ровно 2 раза.

1-й способ: Решать эту задачу можно аналогично предыдущей. Всего исходов может быть 8:

Благоприятных исходов по условию задачи 3 – это «орел-решка-решка», «решка-орел-решка», «решка-решка-орел». И искомая вероятность равна

.

2-й способ. В рамках данной задачи общее число исходов можно определить по формуле

,

где — число подбрасываний монеты (в данном случае ), а 2 – число возможных исходов при подбрасывании монеты (либо «орел», либо «решка»). Таким образом, сразу получаем число исходов .

Число благоприятных исходов можно определить по формуле

,

где — число выпадения «решки» из подбрасываний. В данной задаче и

.

В итоге получаем искомую вероятность

.

Второй способ может существенно сократить время на решение подобных задач, особенно когда речь идет о четырех и более подбрасываний монеты. В этом случае перебирать все варианты и не ошибиться становится трудно, и применение указанных формул существенно облегчает задачу.

Задача 3. В случайном эксперименте монету бросают трижды. Найдите вероятность того, что решка выпадет ровно три раза.

В данной задаче имеется только один благоприятный исход из восьми равновероятных исходов:

Следовательно, искомая вероятность равна

.

Общее число исходов также можно определить по формуле , приведенной в предыдущей задаче.

Задача 4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно один раз.

Будем считать, что выпадение «орла» соответствует началу игры мячом команды «Изумруд». Тогда задача сводится к определению вероятности выпадения «орла» ровно один раз из трех бросаний монеты.

Всего исходов 8 (см. предыдущие задачи). Из них «орел» выпадет ровно один раз в вариантах – это случаи: «орел-решка-решка», «решка-орел-решка», «решка-решка-орел». Следовательно, искомая вероятность равна

.

Источник

Теория вероятностей не так проста как кажется

Что нужно знать о теории вероятностей?

Автор — доцент института религиозных исследований и критической оценки Австралийского католического университета в Мельбурне. Его работы опубликованы в Journal of Philosophy и др.

Азартный игрок, физик-теоретик и присяжный рассуждают о теории вероятностей: какова вероятность выигрыша, радиоактивного распада и виновности подсудимого. Но, несмотря на повсеместность подобных рассуждений, эксперты спорят о самом существовании вероятностей. Это приводит к разногласиям о методах рассуждения: нужно учесть вероятность разногласий о способности когнитивных искажений усугублять, например, к игнорированию доказательств, противоречащих нашим убеждениям. Таким образом, понимание теории вероятностей может помочь нам рассуждать лучше.

Три популярные теории рассматривают вероятности c точки зрения частоты повторения, предрасположенности и степени уверенности. Допустим, я скажу вам, что если вы подбросите монетку, то с вероятностью в 50% выпадет «орёл». Речь в этих теориях идет соответственно о частоте повторения, с которой выпадает «орел»; физических свойствах монеты и тенденции к выпадению «орла»;

ВЕРОЯТНОСТЬ ВЫПАДЕНИЯ «ОРЛА» ПРИ ПЕРВОМ БРОСКЕ СОСТАВЛЯЕТ 75%.

Но у каждой из вышеописанных теорий есть небольшие проблемы. Рассмотрим следующий случай:

Адам подбрасывает симметричную монету*, которая становится невидимой после четвертого броска. Друзья Адама Бет, Чарльз и Дэйв сидят рядом, но с завязанными глазами. После четвертого броска Бет говорит: «вероятность того, что в первый раз выпал «орел» составляет 50%».

Затем Адам говорит друзьям, что «орел» выпал три раза из четырех. Чарльз считает, что вероятность выпадения «орла» при первом броске составляет 75%.

Несмотря на то, что Дэйв владеет той же информацией, что и Чарльз, он говорит: «я не согласен. Вероятность того, что при первом броске выпал «орел» составляет 60%».

*Симметричная монета — математическая монета, используемая в теории вероятностей, лишена многих качеств настоящей монеты. У математической монеты нет цвета, размера, веса и достоинства. Монета с точки зрения теории вероятностей имеет только две стороны, одна из которых называется «орел», а другая —«решка». Монету бросают, и она падает одной из сторон вверх. Никакие другие свойства математической монете не присущи — прим. переводчика.

Частота повторения не соответствует утверждению Бет. «Орел» выпал с частотой три из четырех, но подбросить монету снова нельзя. Кажется, Бет права: вероятность выпадения «орла» при первом броске составляет 50%.

В то же самое время, Чарльз говорил о тенденции к выпадению «орла». Поскольку это симметричная монета, и «орел» и «решка» могут выпасть с одинаковой вероятностью. Кажется, Чарльз оказался прав заявив, что вероятность выпадения «орла» при первом броске составляет 75%. Степень уверенности имеет смысл в двух утверждениях — и Бет и Чарльз уверены в том, что выпал «орел».

Но давайте рассмотрим утверждение Дейва. С одной стороны, когда Дейв говорит, что вероятность выпадения «орла» равна 60%, он врет. Но с другой стороны, если Дейв действительно уверен, что вероятность выпадения «орла» составляет 60%, то он говорит правду, исходя из степени своей уверенности.

Некоторые философы считают, что подобные случаи поддерживают плюралистический подход, при котором учитывается существование самых разнообразных вероятностей. Я же считаю, что следует рассмотреть теорию вероятностей с четвертой точки зрения — уровня поддержки.

Здесь вероятности рассматриваются как совокупность доказательств между утверждениями.

Когда Бет говорит, что «орел» выпадет с вероятностью 50%, она подразумевает, что эта вероятность зависит от ранее полученной информации — например о том, что монета симметричная. Однако, вероятность меняется относительно другой информации. Когда Чарльз говорит, что «орел» выпадет с вероятностью 75%, он имеет в виду, что вероятность равносильна информации о том, что «орел» выпал три раза из четырех. Между тем, Дэйв говорит, что вероятность выпадения «решки» составляет 60% по отношению к той же информации, но поскольку мы знаем, что «орел» выпал три раза из четырех, Дэйв лжет.

Степень уверенности объединяет все три теории и помогает решить существующие проблемы. Она помогает зафиксировать связь между вероятностью и степенью уверенности не идентифицируя их — степень уверенности должна рационально ограничиваться уровнем поддержки. Причина, по которой я должен быть на 50% уверен в том, что выпадет «орел» (при условии, что все, что мне известно о монете — то, что она симметричная), заключается в качестве доказательств, подтверждающих эту гипотезу.

Точно так же, благодаря уровню поддержки, мы знаем, что «орел» выпадал с частотой повторения 75% (что делает выпадение «орла» вероятным на 75% при любом броске). Подобный подход фиксирует связь между частотой повторенияи вероятностью, но не означает, что частота повторения и вероятность — одно и то же. Вместо этого, вероятности могут быть связаны утверждениями о частоте повторения и конкретных людях.

Наконец, тенденция к выпадению «орла» свойственна уровню поддержки, что с одной стороны, говорит о физических свойствах монеты, а с другой о вероятности выпадения «орла» или «решки» — иными словами, данный подход определяет влияют ли физические свойства монеты на ее «поведение». В более широком смысле, причину и следствие связывает предрасположенность — например, описание строения атома и гипотезу о его распаде.

Поскольку все вышеизложенное делает вероятности самостоятельными структурами, наши четыре теории подскажут как определить принцип произведения вероятностей.

Абстрактный объект — объект, созданный какой-либо абстракцией или при посредстве какой-либо абстракции; когнитивно представленный объект познания, репрезентирующий те или иные сущностные аспекты, свойства, отношения вещей и явлений окружающего мира — прим. переводчика.

Скептик может сказать, что подбрасывать монетку легко. Представьте, что вы присяжный. Как определить вероятность совершения убийства подсудимым, чтобы понять существуют ли основания для сомнения в его невиновности?

Ответ: нужно больше думать. Во-первых, задать вопрос: существуют ли доказательства совершения преступления? Мы должны выяснить, насколько убедительны эти доказательства и подтверждают ли они гипотезу о виновности подсудимого. Возможно, наше внимание привлекут отпечатки пальцев на орудии убийства.

Затем следует спросить: можем ли мы математически рассчитать вероятности, чтобы в свете доказательств опровергнуть вероятность нашей гипотезы, заменив ее более приемлемой? Теперь нас интересует вероятность причины-следствия — обвиняемый совершил убийство (причина), его отпечатки пальцев обнаружили на орудии убийства (следствие). позволяет вычислить роль трех дополнительных вероятностей: априорной вероятности причины, вероятности следствия, вызванного этой причиной, и вероятности следствия без причины.

Так как это относится к любой имеющейся у нас информации, первая вероятность (причина) определена тем, что нам известно о мотивах и возможностях подсудимого. Мы можем разобраться с третьей вероятностью (следствие без причины), разбив вероятность невиновности подсудимого на другие возможные причины смерти жертвы; узнать какова вероятность каждой из них, а так же с какой вероятностью отпечатки пальцев подсудимого могут попасть на орудие убийства. В конечном итоге, мы определим вероятность того, что другие вероятности больше не «разбиваются».

Теперь мы можем вывести общие принципы для определения вероятностей, либо опереться на интуитивные суждения, как в случае с подбрасыванием монеты.

Рассуждения о преступниках, а не о монетах, вряд ли приведут к взаимодействию вероятностей. Но альтернативы нет. Просто собирая дополнительную информацию мы не разрешим разногласия об истинности той или иной гипотезы. Добиться прогресса можно только путем философского осмысления огромного количества вероятностей, имеющейся информации и того, насколько она поддерживает одну вероятность по сравнению с другой.

Источник