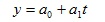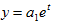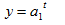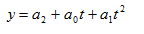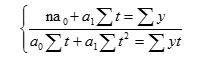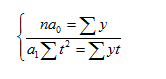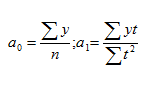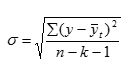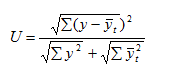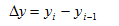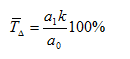Что определяют методом динамического ряда тест

Что определяют методом динамического ряда тест

1.Что такое динамический ряд?

1. Динамический ряд—это множество единиц изучаемого явления, объединенных общими свойствами и подвергающихся дальнейшему изучению.

2. Динамический ряд – это величина, отображающая относительные размеры социально-экономических явлений.

3. Динамический ряд—это упорядоченная совокупность данных, в которых каждому значению признака (варианте или интервалу) соответствует определённое значение частоты или частости.

4. Динамический ряд—это ряд числовых значений признака, представленных в хронологической последовательности и отражающий меру развития явления и процесса, за определённый период времени или на отдельные даты.

5. Динамический ряд—это относительно количественный показатель, получаемый путём сопоставления совокупностей, состоящих из несоизмеримых элементов( не поддающихся прямому суммированию) и отражающих изменение во времени или в пространстве.

2.В зависимости от времени, к которому относится динамический ряд различают:

1. Моментные динамические ряды.

2. Детерминированные динамические ряды.

3. Интервальные динамические ряды.

4. Сложносоставные динамические ряды.

5. Динамические ряды с абсолютными величинами.

3. К механическим приёмам выравнивания относится:

1. Метод по среднему абсолютному приросту.

2. Метод укрупнения периодов.

3. Метод наименьших квадратов.

4. Метод скользящей средней.

5. Метод по среднегодовому темпу роста.

4. Какой из аналитических приёмов выравнивания является наиболее распространенным?

1. По среднему абсолютному приросту.

2. По среднегодовому темпу роста.

3. Метод наименьших квадратов.

4. Метод скользящей средней.

5. Метод укрупнения периодов.

5. В зависимости от величин, которыми представлены уровни динамического ряда, различают динамические ряды:

Источник

Динамические ряды — краткое руководство по анализу изменений явлений во времени

Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.

Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.

Целью анализа динамических рядов является:

Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).

Типы динамических рядов:

а) простые (уровень ряда выражен абсолютными числами);

б) сложные (уровень ряда выражен обобщающими коэффициентами).

а) моментные (данные собираются на определенный момент времени);

б) интервальные (данные собираются за определенный период времени).

а) с выраженной тенденцией (r =0,7 — 1,0);

б) с неустойчивой тенденцией (r =0,3 — 0,69);

в) с отсутствием тенденции ( r = 0 — 0,29).

Основное требование, предъявляемое к анализируемым динамическим ря­дам, заключается в сопоставимости их уровней. Для оценки сопоставимости прово­дят предварительный анализ полученных данных по следующим критериям:

Методика анализа динамических рядов

Методика аналитики предусматривает выполнение последовательных действий:

Способы выравнивания динамических рядов

Чтобы произвести выравнивание динамических рядов потребуются следующие действия:

При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:

а) линейная зависимость:

б) экспоненциальная зависимость:

в) показательная зависимость:

г) параболическая зависимость:

у – теоретический уровень;

t – временной интервал.

где у — уровни фактического ряда;

n — количество уровней;

t — порядковый номер временного периода.

При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:

Отсюда находим параметры уравнения:

Подставляя в уравнение у = а₀ + а₁t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.

При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обуслов­лено как случайными колебаниями, так и неправильно подобранным аппроксими­рующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.

Оценка точности аппроксимации возможна с помощью нахождения

Для получения точной оценки необходимо найти такие величины:

а) коэффициент вариации:

где у- фактический уровень ряда;

y_t — теоретический уровень ряда;

k- число параметров уравнения;

n- число уровней ряда.

Аппроксимация считается точной при C_v не более 15%.

б) коэффициент расхождения Тейла:

где у — фактический уровень ряда;

y_t — теоретический уровень ряда.

Аппроксимация считается точной при U не более 5%

После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факто­ров и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.

Вычисление основных показателей динамического ряда

Алгоритм вычислений ведущих параметров динамических рядов:

yi- текущий уровень (сравниваемый);

у_i-1— базисный уровень (с каким сравнивают);

t- период времени, в течение которого уровень предполагается неизменным.

1.Абсолютный прирост (убыль) :

3.Темп прироста (относительная скорость), темп убыли :

4.Средний темп прироста (убыли):

где а₀; а₁ — параметры уравнения;

k = 1 при нечетном ряде;

k = 2 при четном ряде.

5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.

Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!

Источник