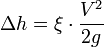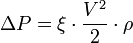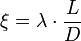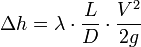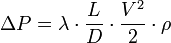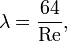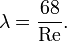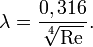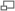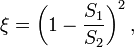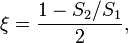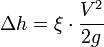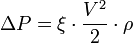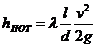Что определяется по формуле дарси вейсбаха и как записываются эти формулы

10.04.202223.04.2022 admin 0 Comments

Формула Дарси-Вейсбаха

Формула Дарси — формула, определяющая потери напора или потери давления на гидравлических сопротивлениях:

Формула Дарси, определяющая потери давления на гидравлических сопротивлениях, имеет вид:

Содержание

Формула Дарси-Вейсбаха

где λ — коэффициент потерь на трение по длине.

Тогда формула Дарси приобретает вид:

или для потери давления:

Последние две зависимости получили название формулы Дарси-Вейсбаха.

Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D представляет собой гидравлический диаметр.

Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.

Определение коэффициента потерь на трение по длине

Коэффициент λ определяется по разному для разных случаев.

Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле:

Иногда для гибких труб в расчётах приниают

Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:

Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).

Определение коэффициента Дарси для местных сопротивлений

К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.

1. При внезапном расширении трубы:

где S₁ и S₂ — площади поперечного сечения трубы, соответственно перед расширением и после него.

2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:

где S₁ и S₂ — площади поперечного сечения трубы, соответственно, перед сужением и после него.

3. При постепенном сужении трубы (конфузор):

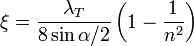
где 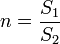— степень сужения; λ_T — коэффициент потерь на трение по длине при турбулетном режиме.

4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).

См. также

Литература

Полезное

Смотреть что такое «Формула Дарси-Вейсбаха» в других словарях:

Формула Дарси — Формула Вейсбаха[1] в гидравлике эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом (англ.) в 1855… … Википедия

ДАРСИ — ВЕЙСБАХА ФОРМУЛА — (в гидравлике), определяет величину потерь напора на трение при движении жидкости в трубах: hv=(ll/d)(v2/2g), где l коэфф. гидравлич. трения, l и d длина и диаметр трубы, ч ср. скорость течения жидкости, g ускорение свободного падения. Коэфф. l… … Физическая энциклопедия

Формула Шези — Формула Шези формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока. Опубликована французским инженером гидравликом… … Википедия

Формула Прони — Формула Прони это исторически важная формула в гидравлике, применявшаяся для расчётов потерь напора на трение при течении жидкости по трубам. Это эмпирическая формула, полученная французом Гаспаром де Прони в XIX веке: где hf потери… … Википедия

Дарси, Анри — Анри Дарси Henry Darcy Дата рождения … Википедия

Формула Борда — В гидродинамике, формула (теорема) Борда Карно это эмпирическая формула, описывающая потери энергии (или напора) жидкости, происходящие при местном расширении потока. Эта формула, в отличие от уравнения Бернулли для идеальной жидкости … Википедия

Гидравлические потери — или гидравлическое сопротивление безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2].… … Википедия

Диффузор (гидроаэродинамика) — У этого термина существуют и другие значения, см. Диффузор. Диффузор (в гидроаэродинамике) часть канала (трубы), в которой происходят замедление (расширение) потока. При этом перепад статических давлений на диффузоре может быть меньше, чем… … Википедия

Гидравлический диаметр — Гидравлический диаметр мера эффективности русла в пропускании потока жидкости. Чем меньше гидравлический диаметр, тем большее сопротивление потоку оказывает русло (при одинаковой площади поперечного сечения потока). Определяется по формуле … Википедия

Источник

Уравнение Дарси-Вейсбаха и его анализ

Формула Дарси — формула, определяющая потери напора или потери давления на гидравлическихсопротивлениях:

· Δh — потери напора на гидравлическом сопротивлении;

· ξ — коэффициент потерь (коэффициент Дарси);

· V — средняя скорость течения жидкости;

· g — ускорение свободного падения;

· величина 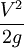называется скоростным напором.

Формула Дарси, определяющая потери давления на гидравлических сопротивлениях, имеет вид:

· ΔP — потери давления на гидравлическом сопротивлении;

· ρ — плотность жидкости.

Формула Дарси-Вейсбаха, применяемая для определения гидравлических потерь при расчете длинных трубопроводов, записывается так:

h_i = λ×l/4R×v 2 /2g

Поясните физический смысл величин, входящих в формулу, и охарактеризуйте их влияние на величину гидравлических потерь в трубопроводе.

Величины, входящие в формулу Дарси-Вейсбаха:

λ – коэффициент гидравлических потерь на трение, зависящий от числа Рейнольдса;

l – длина трубопровода – чем длиннее трубопровод, тем больше потери;

R – гидравлический радиус трубы – чем больше диаметр трубы, тем меньше потери;

v – скорость движения жидкости в трубопроводе – зависимость гидравлических потерь на трение от скорости квадратическая, т. е. увеличение скорости в 2 раза приводит к увеличению потерь на трение в 4 раза и т. п.;

g – ускорение свободного падения – выполняет функцию постоянного коэффициента.

В круглых трубах является эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:

Графики Никурадзе и Мурина для коэффициента гидравлического трения

Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:

Область ламинарного режима (I). В области ламинарного режима (т.е. при Re

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Источник

ДАРСИ — ВЕЙСБАХА ФОРМУЛА

Смотреть что такое «ДАРСИ — ВЕЙСБАХА ФОРМУЛА» в других словарях:

Формула Дарси-Вейсбаха — Формула Дарси формула, определяющая потери напора или потери давления на гидравлических сопротивлениях: где Δh потери напора на гидравлическом сопротивлении; ξ коэффициент потерь (коэффициент Дарси; V средняя скорость… … Википедия

Дарси, Анри — Анри Дарси Henry Darcy Дата рождения … Википедия

Источник

Формула Дарси — Вейсбаха

Формула Вейсбаха [1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена шаблон не поддерживает такой синтаксис в 1855 году):

Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:

Тогда формула Дарси приобретает вид:

Δ h = λ ⋅ L D ⋅ V 2 2 g <\displaystyle \Delta h=\lambda \cdot <\frac >\cdot <\frac ><2g>>>

или для потери давления:

Δ P = λ ⋅ L D ⋅ V 2 2 ⋅ ρ <\displaystyle \Delta P=\lambda \cdot <\frac >\cdot <\frac ><2>>\cdot \rho >

Иногда для гибких труб в расчётах принимают

1. При внезапном расширении трубы:

2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:

3. При постепенном сужении трубы (конфузор):

ξ = λ T 8 sin ⁡ α / 2 ( 1 − 1 n 2 ) <\displaystyle \xi =<\frac <\lambda _><8\sin <\alpha /2>>>\left(1-<\frac <1>>>\right)> ,

Исторически формула Дарси — Вейсбаха была получена как вариант формулы Прони; такой вариант был получен французом Анри Дарси. В дальнейшем она была преобразована в форму, используемую сегодня, саксонцем Юлиусом Вейсбахом в 1845 году.

Источник

СОДЕРЖАНИЕ

Форма потери давления

где потеря давления на единицу длины Δ p / L (Единицы СИ: Па / м ) зависит от:

Форма потери напора

Δ h = потеря напора из-за трения трубы по данной длине трубы (единицы СИ: м); g = местное ускорение свободного падения (м / с 2 ).

Полезно представить потерю напора на длину трубы (безразмерную):

Следовательно, уравнение Дарси – Вайсбаха также можно записать в терминах потери напора:

По объемному расходу

Связь между средней скоростью потока и объемным расходом Q определяется следующим образом:

Q = объемный расход (м 3 / с), A = Смачиваемая площадь поперечного сечения (м 2 ).

Тогда уравнение Дарси – Вейсбаха через Q имеет вид

Форма напряжения сдвига

Среднее напряжение сдвига стенки τ в трубе или открытом канале выражается через коэффициент трения Дарси – Вайсбаха как

Коэффициент трения Дарси

На рисунке 1 показано значение f _D, измеренное экспериментаторами для множества различных жидкостей в широком диапазоне чисел Рейнольдса и для труб с различной высотой шероховатости. В этих данных встречаются три основных режима течения жидкости: ламинарный, критический и турбулентный.

Ламинарный режим

Для ламинарных (гладких) течений следствием закона Пуазейля (который вытекает из точного классического решения для потока жидкости) является то, что

Фактически, потери на трение в ламинарном режиме более точно охарактеризованы как пропорциональные скорости потока, а не пропорциональны квадрату этой скорости: можно было бы рассматривать уравнение Дарси – Вейсбаха как не совсем применимое в ламинарном режиме потока.

В ламинарном потоке потери на трение возникают из-за передачи количества движения от текучей среды в центре потока к стенке трубы через вязкость текучей среды; в потоке нет вихрей. Обратите внимание, что потери на трение нечувствительны к высоте шероховатости трубы ε : скорость потока в окрестности стенки трубы равна нулю.

Критический режим

Для чисел Рейнольдса в диапазоне 2000 поток неустойчивый (сильно меняется со временем) и изменяется от одного участка трубы к другому (не «полностью развит»). Течение связано с зарождающимся образованием вихрей; это не совсем понятно.

Турбулентный режим

Для числа Рейнольдса больше 4000 поток является турбулентным; сопротивление потоку следует уравнению Дарси – Вайсбаха: оно пропорционально квадрату средней скорости потока. В области много порядков величины Re ( 4000 8 ) коэффициент трения изменяется менее чем на один порядок величины ( 0,006 ). В турбулентном режиме потока характер потока можно далее разделить на режим, при котором стенка трубы является фактически гладкой, и режим, в котором высота шероховатости является заметной.

Гладкотрубный режим

Когда поверхность трубы гладкая (кривая «гладкая труба» на рисунке 2), изменение коэффициента трения с Re можно смоделировать уравнением сопротивления Кармана – Прандтля для турбулентного потока в гладких трубах с соответствующими параметрами.

В уравнении сопротивления Кармана – Прандтля f _D может быть выражено в замкнутой форме как аналитическая функция от Re с помощью W- функции Ламберта :

Режим грубой трубы

Для иллюстрации построить функцию шероховатости B :

B ( р * ) знак равно 1 1,930 ж D + бревно ⁡ ( 1,90 8 ⋅ ε D ) <\ displaystyle B (R _ <*>) = <\ frac <1><1.930 <\ sqrt >>>>> + \ log \ left ( <\ frac <1.90><\ sqrt <8>>> \ cdot <\ frac <\ varepsilon>> \ right)>

Рисунок 3 показывает зависимость B от R _∗ для грубых данных по трубам Никурадсе, Шоклинг и Лангеландсвик.

Подгонка к этим данным при переходе от гладкого потока в трубе к грубому потоку в трубе использует экспоненциальное выражение в R _∗, которое обеспечивает правильное поведение при 1 (переход от режима гладкой трубы к режиму шероховатой трубы):

Соотношение Коулбрука – Уайта соответствует коэффициенту трения функцией вида

Расчет коэффициента трения по его параметризации

Прямой расчет, когда известны потери на трение S

ж D знак равно 2 грамм S D ⟨ v ⟩ <\ displaystyle <\ sqrt >>> = <\ frac <\ sqrt <2gSD>> <\ langle v \ rangle>>>

теперь мы можем выразить Re √ f _D :

Путаница с коэффициентом трения Фаннинга

Обратите внимание, что

Δ п знак равно ж D ⋅ L D ⋅ ρ ⟨ v ⟩ 2 2 знак равно ж ⋅ L D ⋅ 2 ρ ⟨ v ⟩ 2 <\ displaystyle \ Delta p = f _ <\ mathrm > \ cdot <\ frac > \ cdot <\ frac <\ rho <\ langle v \ rangle>^ <2>> <2>> = f \ cdot <\ frac > \ cdot <2 \ rho <\ langle v rangle>^ <2>>>

Какой коэффициент трения отображается на диаграмме Муди, можно определить путем проверки, если издатель не включил формулу, описанную выше:

История

Вывод на основе анализа размеров

Практическое применение

Преимущества

Точность и универсальность Darcy-Weisbach делают его идеальной формулой для измерения расхода в трубопроводах. Преимущества уравнения заключаются в следующем:

Источник

Что и для чего?

Что определяется по формуле дарси вейсбаха и как записываются эти формулы

Формула Дарси-Вейсбаха

Формула Дарси-Вейсбаха

Содержание

Формула Дарси-Вейсбаха

Определение коэффициента потерь на трение по длине

Определение коэффициента Дарси для местных сопротивлений

См. также