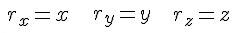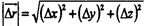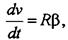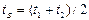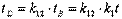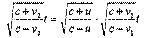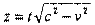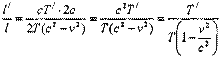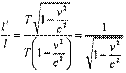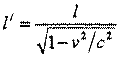Что определяет положение точки в пространстве
Кинематика. Задание положения точки.
Положение точки в пространстве можно задать двумя способами: координатным и векторным.
При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:
Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).
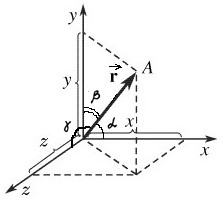
Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор 
Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.
Когда точка М движется, радиус-вектор 



Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций rx, ry, rz на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:
Здесь за 

Из этих уравнений видно, что между координатным и векторным способами задания положения точки существует связь.
Что определяет положение точки в пространстве
Движение. Виды движений. Описание движения. Система отсчета.
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.
А) Равномерное прямолинейное движение материальной точки.
Б) Равноускоренное прямолинейное движение материальной точки.
В) Движение тела по дуге окружности с постоянной по модулю скоростью.
Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.
1. Векторный способ описания движения
ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.
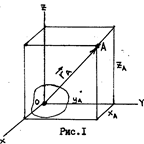
Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.
При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.
В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.
2. Координатный способ описания движения
ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.
В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.
Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )
Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: rx = x , ry = y , rz = z .
3. Естественный способ описания движения
ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.
Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.
Что определяет положение точки в пространстве
§ 7. Три способа задания положения точки в пространстве
1. Координатный способ.
2. Векторный способ задания положения точки на плоскости и в пространстве.
Определение. Радиус-вектором
некоторой точки пространства называется вектор, проведённый из начала координат в данную точку пространства.
Радиус-вектор также однозначно определяет положение точки в пространстве, так как он указывает, в каком направлении расположена точка, а модуль этого вектора указывает, на каком расстоянии находится точка от начала координат.
Проекции радиуса-вектора на оси координат равны координатам конца этого вектора (см. рис. выше).
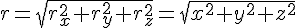
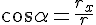
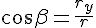
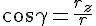
3. Естественный способ задания положения точки.
Он применяется тогда, когда известна траектория, по которой движется точка.
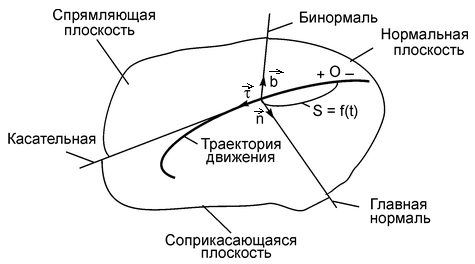
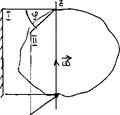
На траектории выбирают начало координат, а также положительное и отрицательное направление отсчёта дуговых координат. Векторные величины в этом случае проецируются на так называемые естественные оси координат: нормаль 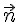
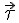
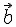
Начало естественных осей координат совмещают с той точкой траектории, через которую в данный момент проходит движущаяся точка. Касательную проводят в положительном направлении отсчёта дуг. Нормаль проводят перпендикулярно касательной и вовнутрь вогнутости траектории. Бинормаль направляют перпендикулярно плоскости, в которой расположены векторы 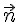
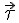
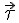
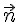
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
Построение ортогональных проекций точек
Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.
По заданному комплексному чертежу точек A и B необходимо:
Определение координат точек по их проекциям
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно Aх, Aу. Координата х для т. A равна длине отрезка AхO со знаком плюс, так как Aх лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка AуO со знаком минус, так как т. Aу лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A» имеет координаты х и z. Опустим перпендикуляр из A» на ось z и найдем Az. Координата z точки A равна длине отрезка AzO со знаком минус, так как Az лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).
Построение проекций точек
Точки A и B в плоскости П3 имеют следующие координаты: A»’ (y, z); B»’ (y, z). При этом A» и A»’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B» и B»’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса AуO. После этого проведем перпендикуляр из Aу до пересечения с перпендикуляром, восстановленным из точки A» к оси z. Точка пересечения этих двух перпендикуляров определяет положение A»’.
Точка B»’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B» к оси z. Точка пересечении этого перпендикуляра с осью z есть B»’.
Определение положения точек в пространстве
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П1, П2 и П3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П2.
| Октанты | Знаки координат | ||
| x | y | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Построение наглядного изображения точек в системе плоскостей П1, П2, П3
Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П1, П2, П3, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.
Определение положения точки в пространстве.
Определение положения точки в пространстве.
 |
Для описания движения точки, т.е. изменения ее положения с течением времени, прежде всего, надо в любой момент времени указать ее местоположение координатным или векторным способом.
 |
Таким образом, зная координаты точки, можно определить величину (1) радиус-вектора, и его направление в пространстве по так называемым направляющим косинусам (2), (3) и (4).
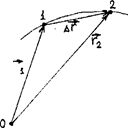
Для определения характеристик движения вводят три вектора: перемещения, скорости и ускорения.
ВЕКТОР ПЕРЕМЕЩЕНИЯ.
Для определения перемещения точки в пространстве вводят вектор перемещения.
 |
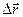
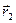

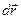

Вектор перемещения за конечный промежуток времени в общем случае не совпадает с направлением движения.
ВЕКТОР СКОРОСТИ.
Вектором скорости называют вектор, определяющий быстроту и направление движения.
 |
Вектором истинной (мгновенной) скорости называют предел, к которому стремится значение вектора средней скорости при бесконечном убывании промежутка времени:
Так как при движении тела в общем случае изменяются все три его координаты, часто бывает удобным рассматривать скорость движения точки вдоль отдельных координатных направлений (компоненты или составляющие вектора скорости). Компоненты средней скорости равны:
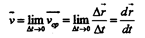 |
Компоненты же мгновенной скорости определяются как
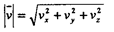 |
 |
 |
ВЕКТОР УСКОРЕНИЯ.
 |
 |
Вектором ускорения называют вектор, определяющий быстроту и направление изменения вектора
скорости. Аналогично определениям для вектора скорости вводятся понятия среднего и мгновенного
Ускоренное движение Замедленное движение

Двигаясь вдоль траектории, за промежуток времени Dt точка проходит путь DS скорость ее изменяется от J до J1, при этом J1 составляет угол Da (альфа) с осью Ot. По определению мгновенного ускорения:
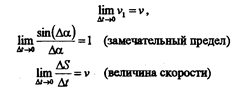 |
 |
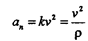
С учетом этих замечаний выражение для нормальной составляющей вектора ускорения принимает вид
Для выяснения физического смысла ускорения рассмотрим два частных случая движения.
Равномерное криволинейное движение (V=const, k<>0). В этом случае, как видно из (14) и (16),
 |
Кинематика твердого тела.
Для нахождения кинематического закона движения, т.е. r=r(t) или х = х(t), у=y(t), z=z(t) надо найти закон движения каждой точки тела, т.е. решить бесконечно большое число уравнений, что сопряжено с непреодолимыми математическими трудностями. Абсолютно твердое тело – тело у которого расстояние между двумя любыми точками остается постоянно при движении.
Числом степеней свободы называют число независимых механических координат полностью и однозначно определяющих положение тела в пространстве. Или: число независимых механических движений, которые одновременно может совершать тело.
Из таких определений следует, что число степеней свободы для свободной материальной точки равно 3. Для совокупности из n невзаимодействующих между собой точек число степеней свободы равно 3n.
Иначе говоря, для точки, движущейся по поверхности, число степеней свободы равно 2. Для точки, движущейся вдоль линии, число степеней свободы равно 1. Рассмотрим теперь систему точек, связанных жесткими связями. Пусть таких точек 2 (рис. 7). Для определения положения одной из точек системы в пространстве нужно указать 3 координаты, т.е. эта часть системы обладает 3-мя степенями свободы. Если эту точку закрепить неподвижно, у системы будет отнято 3 степени свободы. Вторая точка при этом может двигаться только по поверхности сферы, т.е. обладает 2-мя степенями свободы. Следовательно, вся система обладает 5-ю степенями свободы.
Аналогично определяется число степеней свободы для системы, состоящей из трех жестко связанных между собой точек (рис. 8). Если одну из точек системы закрепить, у системы отнимается 3 степени свободы При закреплении второй точки дополнительно отнимается еще а степени свободы При этом третья точка сможет двигаться только вдоль линии, т.е. обладает одной степенью свободы. поэтому вся система обладает 6-ю степенями свободы.
Вращательным называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными в пространстве. Прямая, проходящая через неподвижные точки тела, называются осью вращения. При вращательном движении все точки тела движутся в параллельных плоскостях, описывая концентрические окружности, центры которых лежат на оси вращения.
Быстрота вращения определяется угловой скоростью.
 |
Средней угловой скоростью называют величину:

 |
для определения w как вектора необходимо угол поворота (угловое перемещение) также определять как вектор. Вектором углового перемещения называют вектор, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против хода часовых стрелок. По такому определению вектор угловой скорости равен:
В случае вращения тела, показанном на рис. 10, вектор угловой скорости направлен вверх вдоль оси вращения.
 |
Вектором среднего углового ускорения называют вектор

Сила.
Изменение состояния тела происходит в результате взаимодействий, которые приводят к изменению, как внутреннего состояния тел, так и состояния их движения. Количественной мерой взаимодействий, приводящих к изменению состояний тел, является сила.
Линия, вдоль которой направлена сила, называется линией действия силы.
Совокупность сил, приложенных к телу, называют системой сил.
Если под действием системы сил, приложенных к телу, оно может пребывать в состоянии покоя, система называется уравновешенной
Сила, равная по величине равнодействующей и противоположно ей направленная, называется уравновешивающей.
Силы взаимодействия между телами одной и той же системы называются внутренними.
Силы взаимодействия с телами, не входящими в состав данной системы называются внешними.
Силы, приложенные в одной точке тела, называются сосредоточенными.
Силы, приложенные ко всем точкам поверхности или объема тела, называются распределенными.
Основной закон динамики.
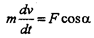
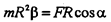
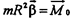 |
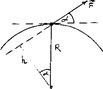
Rcosa=h (плечо силы относительно центра окружности).
Следовательно, величина mR 2 определяет инертные свойства тела при вращательном движении. Эта величина I=mR 2 называется моментом инерции тела (точки). С учетом сказанного основной закон динамики для вращательного движения записывают в виде:
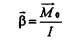 |

11. движение тел в поле центральных сил.
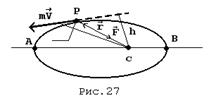 |
Центральными называют силы, линии действия которых проходят в своё время через один и тот же центр. Примером таких сил могут служить силы гравитационного взаимодействия между планетами Солнечной системы.
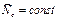
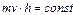 |
условия постоянства направления следует, что орбита планеты плоская, т.е. она движется всё время в одной и той же плоскости.
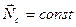
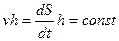 |
Считая массу планеты постоянной, можно далее записать:
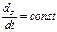 |
Из рисунка видно, что h*dS равно удвоенной площади, ометаемой радиус-вектором планеты за промежуток времени dt.Обозначив эту площадь dσ, получим:
т.е. площадь, ометаемая радиус-вектором планеты в единицу времени (секториальная скорость) постоянна.
Постулаты Эйнштейна.
В основе специальной теории относительности, прежде всего, лежит факт постоянства скорости света в различных системах отсчета, что противоречит классическому закону сложения скоростей. Кроме того, нет никаких оснований считать, что механические опьггы позволят отличить одну инициальную систему отсчета от другой. Это позволило Эйнштейну сформулировать исходные постулаты специальной теории относительности.
Постулат о постоянстве скорости света: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источника и приемника света.
Постулат относительности (общефизический принцип относительности): Никакими физическими опытами нельзя отличить одну инерциальную систему отсчета от другой. Наряду с этими постулатами Эйнштейн ввел принцип синхронизации часов, имеющий такое же значение в теории относительности, как и сформулированные выше постулаты.
Для того, чтобы одинаковые по устройству часы А и В (рис.31)
 |
 |
«Радиолокационный» метод (метод коэффициента «k «).
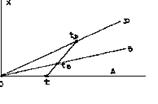
Движение тел можно графически представлять диаграммами x=x(t). В случае скоростей, сравнимых со скоростью света, масштаб х и t выбирается таким, что траектория светового сигнала («световая линия») делит координатный угол пополам. Если же тело движется со скоростью, меньшей скорости света, угол наклона его траектории к оси t меньше 45°.
Предположим, что две инерциальные системы отсчета А и В находятся в относительном движении. Систему А условно считаем неподвижной. В исходный момент времени системы полностью совпадали. В этот момент осуществляется синхронизация подвижных и неподвижных часов и на них устанавливаются нулевые показания. Далее система В удаляется от А со скоростью v v1. В момент времени t (пo часам А) в системе А производится световая вспышка, сигнал от которой достигает
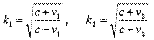 |
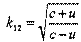
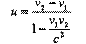
откуда: Это и есть выражение для относительной скорости.
19 . Сравнение поперечных размеров тел.
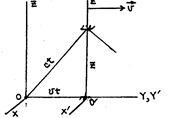 |
В подвижной системе, связанной с подвижными часами, длина их равна: z’=ct’
т.е. поперечные размеры (по отношению к направлению движения) тел одинаковы в обеих системах отсчета: z’=z
Эффект «сокращения» длин.
 |
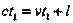
времени t1 по неподвижным часам (рис.35). Тогда:
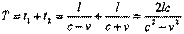
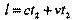
Период световых часов, измеренный в неподвижной системе, равен:
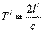
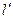 |
Следовательно, продольные размеры тел в любой системе меньше собственных :
20. Преобразования Лоренца.
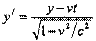
Учитывая, что поперечные размеры тел одинаковы, получаем:
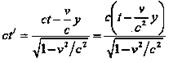
Для сравнения координат у обратимся к предыдущему примеру:
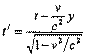
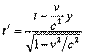
Интервал. Инвариантность интервала.
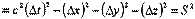
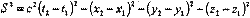 |
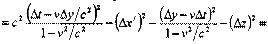
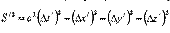
Таким образом, интервал является инвариантом S /2 =S 2
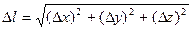
1.Времениподобные интервалы (cΔt > Δl).
2.Пространственноподобные интервалы (cΔt









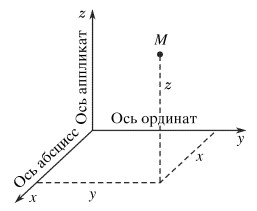
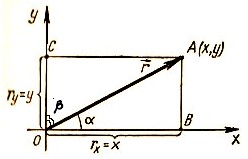
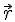 некоторой точки пространства называется вектор, проведённый из начала координат в данную точку пространства.
некоторой точки пространства называется вектор, проведённый из начала координат в данную точку пространства.