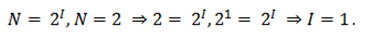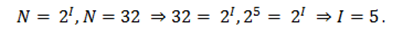Что определяет мощность алфавита информатика
Мощность алфавита: что это и как она определяется?

Методы измерения информации в электронном виде
Мощность алфавита может пригодиться очень многим пользователям в процессе работы. Однако перед тем как дать определение этому термину и разобраться в методах его расчета необходимо немного поговорить о том, как измеряется электронная информация, поскольку это является материальной базой, на основании которой базируется дальнейшая теория.
Каждый человек знает о том, что любая величина имеет свою систему измерений. Например, температура измеряется в градусах, расстояние выражается в метрах, временные интервалы строятся из секунд и так далее. Однако немногие пользователи знают о том, в каких величинах измеряется текстовая информация в электронном виде. Для этих целей в информатике и было создано определение мощность алфавита.
Определение термина
Исходя из того, что значение абсолютно любой величины, известной в наши дни человечеству, является неким параметром, состоящим из набора измерительных единиц, то определение понятию мощности алфавита проще всего сделать следующим образом: мощность алфавита — это количество символов, которое входит в состав любого языка.
Однако это всего-лишь общее определение, которое отражает только поверхностное значение мощности алфавита, поскольку само определение носит более глубокий характер. Чтобы понять всю его суть необходимо разобраться с тем, что представляют собой символы, с точки зрения высоких технологий. Все символы, используемые в компьютере, включают в себя буквы, цифры, знаки препинания и набор специальных символов. Однако это еще не все, поскольку для определения мощности алфавита необходимо еще учитывать и пробел, который предназначен для разделения слов между собой.
Давайте в качестве примера рассмотрим русскую раскладку клавиатуры, которая используется для печати русскоязычного текста и состоит из 34 букв, 10 цифр и 11 дополнительных символов, суммарное количество которых составляет 54, что, в свою очередь, классифицируется как мощность алфавита русской раскладки клавиатуры..
Информационный вес символов
Давайте постепенно продвигаться далее. Мощность алфавита не заключается в одном лишь числе букв и цифр, которые используются в напечатанном тексте. Для определения этого параметра необходим более глубокий подход.
Давайте на секунду задумаемся о том, какой минимальный объем символов входит в состав одной буквы, цифры или специального знака? Правильный ответ — два. Каждый символ в компьютере обладает своим информационным весом, благодаря которому машина способна распознавать какую информацию ввел пользователь. Все дело в том, что машина не способна распознавать информацию в том виде, в котором ее представляют люди. Вместо этого, он использует специальный машинный язык, состоящий из нулей и единиц, при помощи которых происходит преобразование текстовой информации в двоичный код, понятный компьютерной системе.
Что касается информационного веса, то он выражается в битах и является стандартной единицей для измерения информации в электронном виде.
Немного о двоичном коде
Теперь мы имеем более-менее доступным для понимания определением мощности алфавита. Однако для понимания всей глубины теории представления электронной информации машинами необходимо иметь представление о двоичном коде. Давайте рассмотрим этот вопрос на примере мощности алфавита, состоящей из четырех любых символов, каждый из которых имеет вес два бита.
Следуя из всего вышесказанного, четыре символа будут иметь весь четыре бита, восемь — три и так далее. На основании этого принципа и происходит расчет веса текстовой информации, выраженной в электронном виде, компьютерными системами.
Вычисления мощности алфавита и ее практическое использование
С терминологией и основными теоретическими терминами мы разобрались, поэтому теперь давайте рассмотрим какая существует взаимосвязь между мощностью алфавита и его весом. Чтобы более наглядно провести взаимосвязь между ними давайте рассмотрим одну формулу: N=2b, в которой первая переменная соответствует количеству символов, а вторая — количеству знаков, используемых компьютерами в машинном языке.
Из этого математического выражения следует, что 21=2, 22=4, 23=8, 24=16 и так далее. На основании этого можно сделать весьма разумный и обоснованный вывод: число символов, используемых в машинном языке, представляет собой вес символа.
Как измеряется объем информации?
Рассмотренные выше примеры являются очень простыми, на примере которых можно дать общее представление мощности алфавита. Однако на деле все выглядит намного сложнее, поскольку каждый пользователь в процессе набора текста использует не только строчные, но и заглавные буквы, а также различные шрифты, языковую раскладку, знаки препинания, специальные символы, цвета и многое другое. Исходя из этого можно предположить, что общее число всех суммарных символов равняется 256. Поскольку 256 равняется 28 в двоичном коде, то в этом случае вес каждого символа составляет 8 битам или одному байту.
Таким образом, обладая всеми необходимыми параметрами, мы можем рассчитать объем электронной информации. Например, мы напечатали 30 страниц печатной информации, на каждой из которых содержится 50 строк по 60 различных символов. Используя известную нам формулу, производим необходимые вычисления:
— информационный вес одной строки будет равен: 50 х 60 = 3000 байт;
— а весь текст будет весить: 3000 х 50 = 150 000 байт.
Стоит отметить, что конечный результат можно выражать не только в байтах, а переводить стандартную единицу измерения в килобайты, мегабайты и другие. Для этого необходимо величину более младшего порядка разделить на 1024, поскольку именно столько единиц младшей величины образуют старшую единицу измерения.
Заключение
Прочитав эту статью, вы получили общее представление о том, что представляет собой мощность алфавита, а также о методах ее расчета. Однако был рассмотрен исключительно математический подход, в котором не учитываются некоторые другие параметры, основным из которых является смысловая нагрузка. Этот аспект является одним из наиболее важных для понимания, поскольку независимо от объема символов, если они не несут никакой информационной ценности, то его ценность равна нулю. Однако рассчитать вес бессмысленного набора символов все равно можно.
Если говорить в общем, то мощность алфавита, как один из терминов информатики, не представляет собой ничего сложного для понимания. Но многие пользователи пренебрегают этим терминов, поскольку считают его бесполезным, однако, на практике все обстоит совершенно иначе. В наши дни пользователи работают преимущественно с электронной информацией, которая со временем может полностью вытеснить печатную, поэтому необходимо иметь представление о том, как эта информация выражается в машинном виде и каким образом она рассчитывается.
Что такое мощность алфавита, как определить информационный объем
В век развития компьютерных технологий, информатики, систем исчисления и многого другого все перечисленные определения имеют немалое влияние на жизнь человека. Большее количество пользователей не слишком полно разбираются в информатике, поэтому проясним, что означает понятие мощность алфавита, как ее вычислить и применить.
Что это такое?
Понятие «мощность алфавита» лежит в основе изучения информатики. Многочисленный набор символов принято называть — алфавит. Сумма всех символов выбранного языка называется мощностью. Следует вывод: мощность алфавита — это количество символов, которое используется в выбранном языке. Весь перечень используемых значков может содержать числа, различного характера скобки, специальные символы, запятые, двоеточия, точки, пробел и т.д.
Все же обобщенное понятие в информатике не учитывает расчеты информационной величины сообщения, которое содержит знаки препинания, числа и другое. Здесь необходим другой метод. Суть в том, что отдельная литера, цифра или скобка содержит собственный информационный объем данных. По этому информационному коду мозг компьютера опознает, что было напечатано. Машина разбирает введенные данные только в двоичном коде в виде единицы и нуля, в этом и заключается суть компьютерной науки.
В результате выходит, что любой символ можно закодировать путем различной расстановки нулей и единиц. Наименьшая последовательность, которая обозначает какую-либо букву или цифру, содержит всего два элемента. Информационный вес одного символа принято представлять в виде стандартной информационной единицы измерения, наименование которой «бит». Восемь битов равны одному байту.
Формула предназначена для расчета мощности используемого языка, которая обозначается буквой N (информационный вес, или объем), i – количество бит (в единице слова. Т.е. вес символа).
Формулировка теории о количестве информации в набранной фразе: I=K*i. Здесь К – это количество символов в сообщении, I- информационная масса значка.
Количество символов входящих в русский алфавит — 33 буквы. Выходит, что мощность взятого языка N=33. Английский язык содержит 26 букв и его мощность — 26. Но есть и клавиатурный язык, состоящий из букв русского языка и дополнительных знаков: 33 буквы, 10 чисел, 11 знаков препинания, скобки и пробел = 57.
Как определить объем информации в тексте?
Обычно всегда при наборе текста можно использовать жирные, заглавные, и буквы с курсивом, знаки препинания, разнообразные скобы, операции вычисления и т.д. По расчетам получается, что мощность компьютерного алфавита — это 256 символов и вариантов. Следуя формуле Хартли, N=256, тогда масса каждого значка (i) в клавиатурном алфавите равна восьми битам, то есть один байт.
Размер напечатанной фразы нужно вычислять по формуле: V=K⋅log2N, N — это численность символов в алфавите, а количество знаков в напечатанной фразе – K. Например, дан любой текст, который уместился на 30 страницах. На каждой из них расположено по 55 строчек, в них по 65 символов. Получается, что на странице будет 50 х 65= 3 575 байт информации.
Примеры расчета мощности и объема
Сколько символов можно закодировать 3 битами?
Приняв информационный вес символа за байт, требуется рассчитать объем информации напечатанного сообщения:
«Белеет парус одинокий
В тумане моря голубом»
В приведенных двух строчках насчитывается 43 инициала (пробелы считаются, но скобки не учитываются), тогда информационный объем вычисляется по формуле, которая приведен ниже:
Измерение информации. Алфавитный подход к измерению информации. Мощность алфавита. Информационный объем текста
Алфавитный подход к измерению информации Вам хорошо известно, что для измерения таких величин, как, например, расстояние, масса, время, существуют эталонные единицы. Для расстояния — это метр, для массы — килограмм, для времени — секунда. Измерение происходит путем сопоставления измеряемой величины с эталонной единицей. Сколько раз эталонная единица укладывается в измеряемой величине, таков и результат измерения. Следовательно, и для измерения информации должна быть введена своя эталонная единица. Алфавитный подход позволяет измерять информационный объем текста на некотором языке (естественном или формальном), не связанный с содержанием этого текста.
Алфавит. Мощность алфавита
Под алфавитом мы будем понимать набор букв, знаков препинания, цифр, скобок и др. символов, используемых в тексте. В алфавит также следует включить и пробел, т. е. пропуск между словами.
Полное число символов в алфавите принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54:33 буквы + 10 цифр + 11 знаков препинания, скобки, пробел.
Информационный вес символа
При алфавитном подходе считается, что каждый символ текста имеет определенный информационный вес. Информационный вес символа зависит от мощности алфавита. А каким может быть наименьшее число символов в алфавите? Оно равно двум! Скоро вы узнаете, что такой алфавит используется в компьютере. Он содержит всего 2 символа, которые обозначаются цифрами «0» и «1». Его называют двоичным алфавитом. Изучая устройство и работу компьютера, вы узнаете, как с помощью всего двух символов можно представить любую информацию.
Информационный вес символа двоичного алфавита принят за единицу информации и называется 1 бит.
Алфавитный подход к оценке количества информации. Формула Хартли
Вы будете перенаправлены на Автор24
Содержательный подход к оценке количества информации, который мы рассматривали ранее, измеряет ее количество, как уменьшение неопределенности наших знаний.
Однако любое техническое устройство не способно воспринимать непосредственно содержание информации, оно лишь понимает наличие или отсутствие электрических сигналов. Вследствие чего в вычислительной технике вынуждены использовать другой подход к оценке количества информации, который называется алфавитным.
Принцип алфавитного подхода к оценке количества информации
Алфавитный подход строится на принципе, утверждающем, что любое сообщение можно представить в виде кодов с помощью конечной последовательности символов, содержащейся в любом алфавите. Носители информации содержат любые последовательности символов, которые могут храниться, передаваться и обрабатываться как с помощью человека, так и с помощью технических устройств, в частности компьютера. Этот подход описал А.Н. Колмогоров, согласно которому, информативность, заключающаяся в последовательности символов, не может зависеть от содержания самого сообщения, а может определяться лишь минимальным количеством символов, необходимых для ее кодирования. Подобный подход к оценке количества информации носит объективный характер, так как не зависит от получателя, принимающего сообщения. Смысл же сообщений может учитываться только на этапе выбора алфавита кодирования либо не учитываться совсем.
В основу принципа этого подхода лег подсчет числа символов в сообщении, таким образом, важна только длина сообщения и совсем не учитывается его содержание. Однако на длину сообщения может влиять мощность алфавита используемого языка.
Мощность алфавита и информационная емкость. Формула Хартли
Все множество символов, из которых состоит язык, можно традиционно назвать алфавитом. Как правило, под алфавитом понимаются только буквы, но кроме них при написании текстов используются знаки препинания, цифры, скобки, пробелы, их тоже, в свою очередь, можно включить в алфавит.
Например:
Готовые работы на аналогичную тему
При алфавитном подходе считают, что каждый символ текста несет в себе определенную информационную емкость, которая, в свою очередь, зависит от мощности алфавита.
Хартли утверждал, что на количество информации, содержащейся в сообщении, может влиять фактор неожиданности, который, в свою очередь, зависит от вероятности получения сообщения. Если эта вероятность получения сообщения высокая, а неожиданность при этом низкая, то сообщение будет содержать мало полезной для человека информации.
Однако при создании своей формулы Р.Хартли полностью исключил фактор неожиданности. Формула Хартли работает только в том случае, когда появление символов равновероятно и они статистически независимы.
Например, с помощью приведенной формулы можно определить количество информации, которое несет знак в двоичной системе счисления:
Информационная емкость знака двоичной системы составляет 1 бит.
Необходимо определить информационную емкость буквы русского алфавита (без учета буквы «ё»).
Решение:
Представим себе, что текст к нам поступает последовательно, по одному знаку, словно бумажная лента, выползающая из телеграфного аппарата. Предположим, что каждый символ, который появляется на ленте, с равной вероятностью может быть любым символом алфавита. В действительности это не совсем так, но для упрощения примем такое предположение.
Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Количество информации в сообщении можно определить, используя формулу:
Рассмотрим пример решения задачи
Решение. Чтобы решить задачу, для начала определим количество знаков в сообщении и мощность используемого алфавита.
Необходимо определить какое количество информации содержит слово «Привет».
Однако мы не сможем воспользоваться этой формулой, поскольку нам не известно какое количество информации несет один знак ($I$).
Единицы измерения информации
Проведем несложный расчет и получим, что страница содержит:
$50 \cdot 60 = 3000$ байт информации.
Объем же информации, содержащейся в книге:
$3000 \cdot 50 = 150 \ 000$ байт.
Любая система единиц измерения содержит основные единицы и производные от них.
При измерении больших объемов информации на практике широко используются следующие производные от байта единицы, которые приведены в таблице:
Урок информатики и ИКТ «Измерение информации. Алфавитный подход»
Цель урока: познакомить с понятиями: “измерение информации”, “алфавит”, “мощность алфавита”, “алфавитный подход в измерении информации”, научить измерять информационный объём сообщений, с учётом информационного веса символов.
Тип урока: объяснительно-демонстрационный с элементами практикума.
Нагляднось: презентация “Измерение информации” (приложение 1).
Учебная литература: учебник “Информатика”. 8-й класс (базовый курс) И.Г.Семакин, “Информатика” задачник-практикум (1 часть) И.Г.Семакин.
Требования к знаниям и умениям:
II. Проверка домашнего задания.
Задачник-практикум № 1. с. 11 № 2, 5, 8, 11, 19 *.
III. Новый материал.
Процесс познания окружающего мира приводит к накоплению информации в форме знаний.
Как же узнать, много получено информации или нет?
Необходимо измерить объём информации. А как это сделать мы сегодня узнаем.
Получение новой информации приводит к расширению знаний или, как иначе можно сказать, к уменьшению неопределённости знания.
Если некоторое сообщение приводит к уменьшению неопределённости нашего знания, то можно сказать, что такое знание содержит информацию (рисунок 1).
2. Как можно измерить количество информации.
Для измерения различных величин существуют эталонные единицы измерения.
Следовательно, для измерения информации должна быть введена своя эталонная единица.
Существует два подхода к измерению информации:
а) Содержательный (вероятностный). Количество информации связывается с содержанием (смыслом) полученного сообщения или с учётом вероятности событий.
б) Алфавитный. Позволяет измерять информационный объём текста на любом языке (естественном или формальном), при использовании данного подхода объём информации не связывают с содержанием текста, в данном случае, объём зависит от информационного веса символов.
3. Алфавитный подход к измерению информации.
*Алфавит включают и пробел (пропуск между словами).
Например: мощность алфавита русских букв и используемых символов равна 54:
33 буквы + 10 цифр + 11 знаков препинания, скобки, пробел.
Наименьшую мощность имеет алфавит, используемый в компьютере (машинный язык), его называют двоичным алфавитом, т.к. он содержит только два знака “0”, “1”.
Информационный вес символа двоичного алфавита принят за единицу измерения информации и называется 1 бит.
Попробуйте определить объём информационного сообщения:
Информация, записанная на машинном языке, весит:
При алфавитном подходе считают, что каждый символ текста, имеет информационный вес.
Информационный вес символа зависит от мощности алфавита.
С увеличением мощности алфавита, увеличивается информационный вес каждого символа.
Для измерения объёма информации необходимо определить сколько раз информация равная 1 биту содержится в определяемом объёме информации.
1) Возьмём четырёхзначный алфавит (придуманный), (рисунок 2).
Все символы исходного алфавита можно закодировать всеми возможными комбинациями, используя цифры двоичного алфавита.
Получим двоичный код каждого символа алфавита. Для того чтобы закодировать символы алфавита мощность которого равна четырём, нам понадобится два символа двоичного кода.
Следовательно, каждый символ четырёхзначного алфавита весит 2 бита.
Вывод. Весь алфавит, мощность которого равна 8 можно закодировать на машинном языке с помощью трёх символов двоичного алфавита (рисунок 4).
— Как вы думаете, каков информационный объём каждого символа восьмизначного алфавита?
Каждый символ восьмизначного алфавита весит 3 бита.
3). Закодируйте с помощью двоичного кода каждый символ алфавита, мощность которого равна 16.
— Какой можно сделать вывод?
Алфавит из шестнадцати символов можно закодировать с помощью четырёхзначного двоичного кода.
Задача: Какой объём информации содержат 3 символа 16 – символьного алфавита?
Так как каждый символ алфавита мощностью 16 знаков можно закодировать с помощью четырёхзначного двоичного кода, каждый символ исходного алфавита весит 4 бита.
Так как всего использовали 3 символа алфавита мощностью 16 символов, следовательно: 4 бит • 3 = 12 бит
Ответ: объём информации записанный 3 знаками алфавита мощностью 16 символов равен 12 бит.
— Найдите закономерность (рисунок 5)!
— Какой вывод можно сделать?
Информационный вес каждого символа, выраженный в битах (b), и мощность алфавита (N) связаны между собой формулой: N = 2 b
Алфавит, из которого составляется на компьютере текст (документ) состоит из 256 символов.
Этот алфавит содержит символы: строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания и другие символы.
— Узнайте, какой объём информации содержится в одном символе алфавита, мощность которого равна 256.
Вывод. Значит, каждый символ алфавита используемого в компьютере для печати документов весит 8 бит.
Эту величину приняли так же за единицу измерения информации и дали название байт.
1) На каждой странице 50 • 40 = 2000 символов;
2) во всей статье 2000 • 30 = 60000 символов;
3) т.к. вес каждого символа равен 1 байту, следовательно, информационный объём всей статьи 60000 • 1 = 60000 байт или 60000 • 8 = 480000 бит.
— Как видно из задачи байт “мелкая” единица измерения информационного объёма текста, поэтому для измерения больших объёмов информации используются более крупные единицы.
Единицы измерения информационного объёма:
1 килобайт = 1 Кб = 210 байт = 1024 байт
1 мегабайт = 1 Мб = 210 Кб = 1024 Кб
1 гигабайт = 1 Гб = 210 Мб = 1024 Мб
— Попробуйте перевести результат задачи, в более крупные единицы измерения:
60000 байт • 58,59375 Кб
60000 байт • 0,057 Мб
IV. Закрепление изученного.
Задачник-практикум № 1. С. 19 № 19, 20, 22, 23, 25.
V. Подведение итогов.
VI. Домашнее задание.
Задачник-практикум № 1. с. 20 № 21, 24, 26.