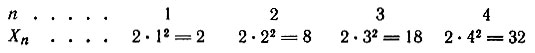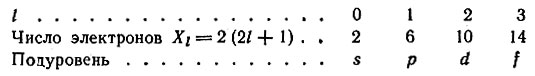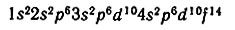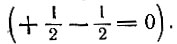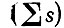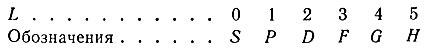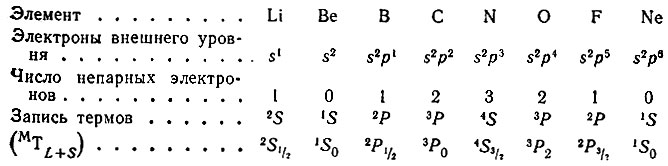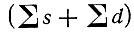Что определяет энергетическое состояние электрона в атоме
Состояние электронов в атоме
Электронное строение атома и энергия электронов
Электронное строение атома определяется энергией электронов, а также вероятностью их нахождения в каждой точке пространства вблизи ядра. Поведение электронов в атоме описывается с помощью квантовой механики, главный постулат которой – все микрочастицы имеют волновую природу, а волны – свойства частиц (корпускулярно – волновой дуализм).
Масса (m) любой частицы и ее скорость (v) связаны с длиной волны (λ) уравнением де Бройля:
Второй постулат квантовой механики говорит о том, что невозможно одновременно точно определить положение и импульс электрона (принцип неопределенности Гейзенберга). Погрешности в определении координаты (Δx) и импульса (Δmv) связаны соотношением:
В-третьих, энергия электронов меняется квантами (порциями).
Поскольку квантовая механика рассматривает вероятность нахождения электрона в пространстве вокруг ядра, а быстродвижущийся электрон может находиться в любой области пространства, то если бы удалось сфотографировать через малые промежутки времени положение электрона в атоме и наложить полученные снимки друг на друга, то получилась бы картина электронного облака.
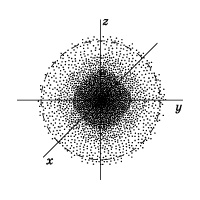
Электронное облако — квантовомеханическая модель, описывающая состояние электрона в атоме. Плотность электронного облака неравномерна (рис. 1). Пространство, вокруг ядра, в котором наиболее вероятно нахождение электрона, называется орбиталью. В нем заключено 90% электронного облака.
Рис. 1. Электронное облако атома водорода с неравномерной плоностью.
Располагаясь на азличных расстояниях от ядра электроны образуют энергетические слои (энергетические уровни). Их нумеруют, начиная от ядра: 1, 2, 3, 4, 5, 6, 7 или обозначают буквами: K, L, M, N, O, P, Q.
Квантовые числа
Состояние электрона в атоме можно описать с помощью четырех квантовых чисел (табл. 1). Целое число n, обозначающее номер уровня, называют главным квантовым числом. Оно характеризует энергию электронов, которые занимают конкретный энергетический уровень. Наименьшая энергия характерна для электронов, максимально близко расположенных к ядру. Число энергетических уровней в атоме определяется номером периода, в котором находится элемент. Наибольшее число электронов на энергетическом уровне можно определить по формуле:
где N – число электронов, n – главное квантовое число.
Таблица 1. Квантовые числа, характеризующие состояние электрона в атоме
Атомы и электроны
Атомно-молекулярное учение
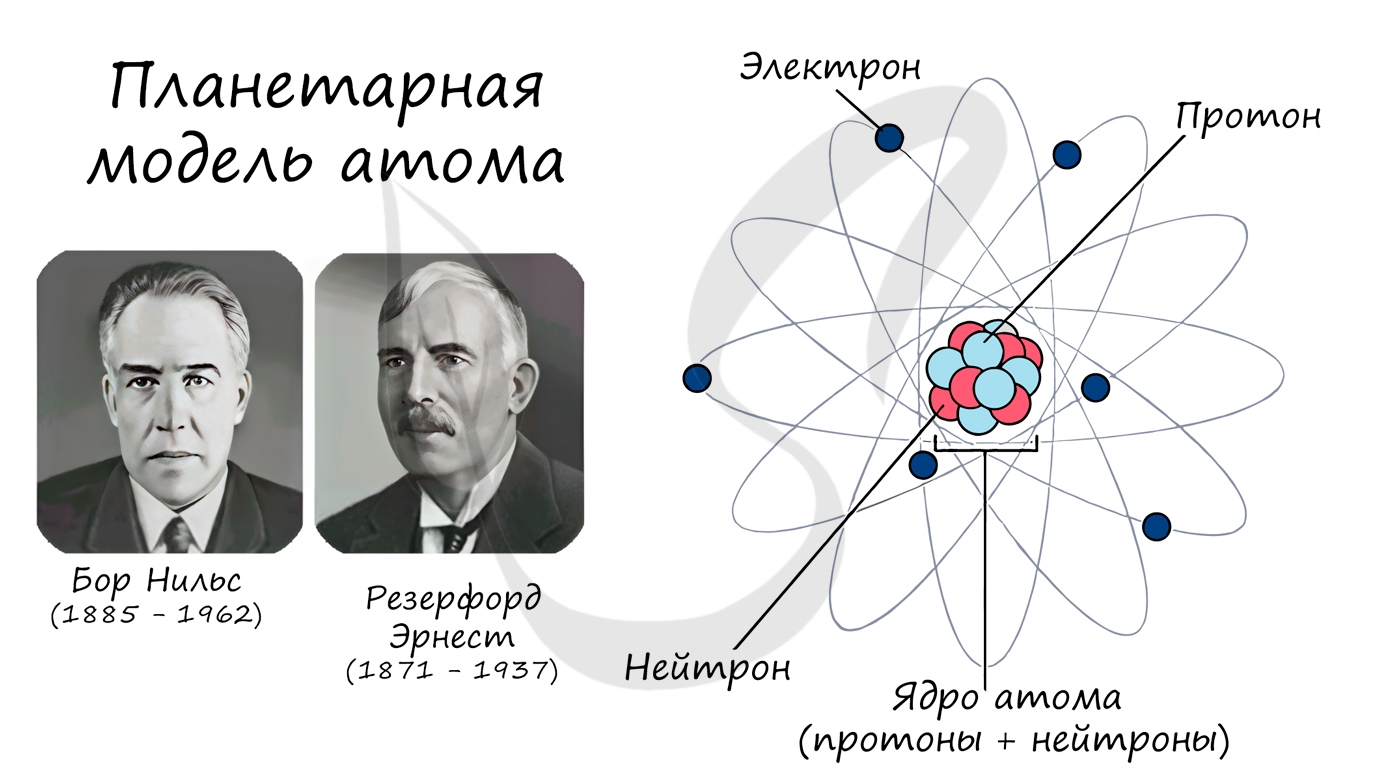
Описываемая модель атома называется «планетарной» и была предложена в 1913 году великими физиками: Нильсом Бором и Эрнестом Резерфордом
Запомните, что в невозбужденном состоянии атом содержит одинаковое число электронов и протонов. Так у кальция (порядковый номер 20) в ядре находится 20 протонов, а вокруг ядра на электронных орбиталях 20 электронов.
Я еще раз подчеркну эту важную деталь. На данном этапе будет отлично, если вы запомните простое правило: порядковый номер элемента = числу электронов. Это наиболее важно для практического применения и изучения следующей темы.
Электронная конфигурация атома
Электроны атома находятся в непрерывном движении вокруг ядра. Энергия электронов отличается друг от друга, в соответствии с этим электроны занимают различные энергетические уровни.
Состоит из s-подуровня: одной «s» ячейки (2s 2 ) и p-подуровня: трех «p» ячеек (2p 6 ), на которых помещается 6 электронов
Состоит из s-подуровня: одной «s» ячейки (3s 2 ), p-подуровня: трех «p» ячеек (3p 6 ) и d-подуровня: пяти «d» ячеек (3d 10 ), в которых помещается 10 электронов
Состоит из s-подуровня: одной «s» ячейки (4s 2 ), p-подуровня: трех «p» ячеек (4p 6 ), d-подуровня: пяти «d» ячеек (4d 10 ) и f-подуровня: семи «f» ячеек (4f 14 ), на которых помещается 14 электронов
Зная теорию об энергетических уровнях и порядковый номер элемента из таблицы Менделеева, вы должны расположить определенное число электронов, начиная от уровня с наименьшей энергией и заканчивая к уровнем с наибольшей. Чуть ниже вы увидите несколько примеров, а также узнаете об исключении, которое только подтверждает данные правила.
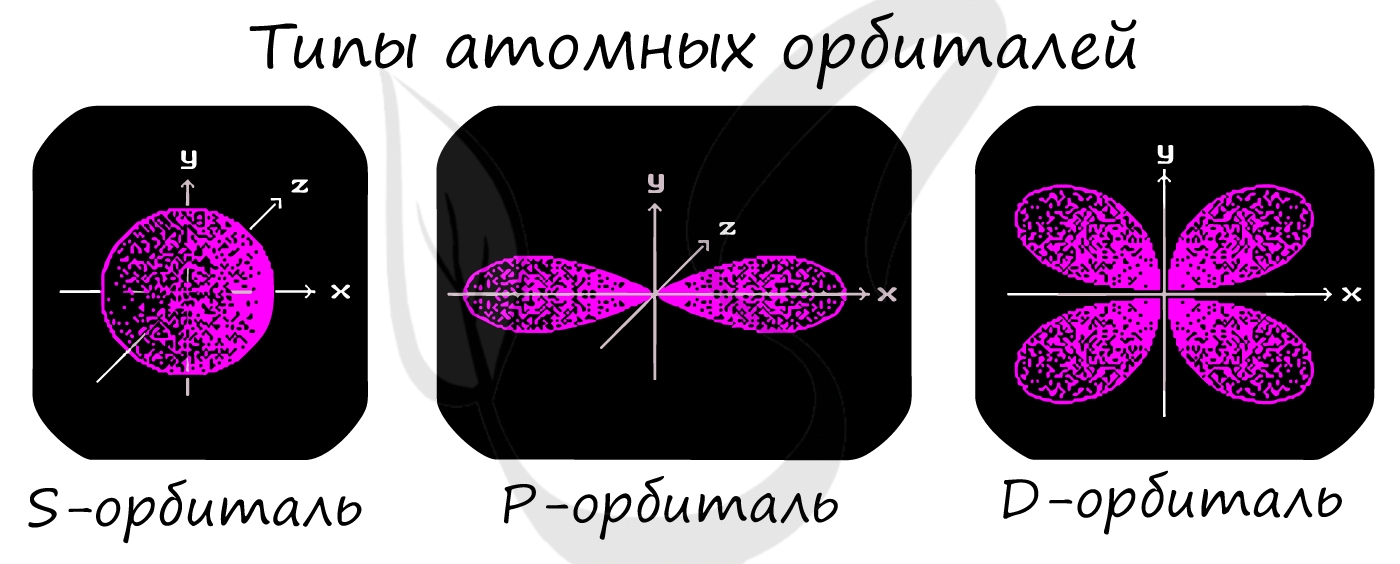
Подуровни: «s», «p» и «d», которые мы только что обсудили, имеют в определенную конфигурацию в пространстве. По этим подуровням, или атомным орбиталям, движутся электроны, создавая определенный «рисунок».
Правила заполнения электронных орбиталей и примеры
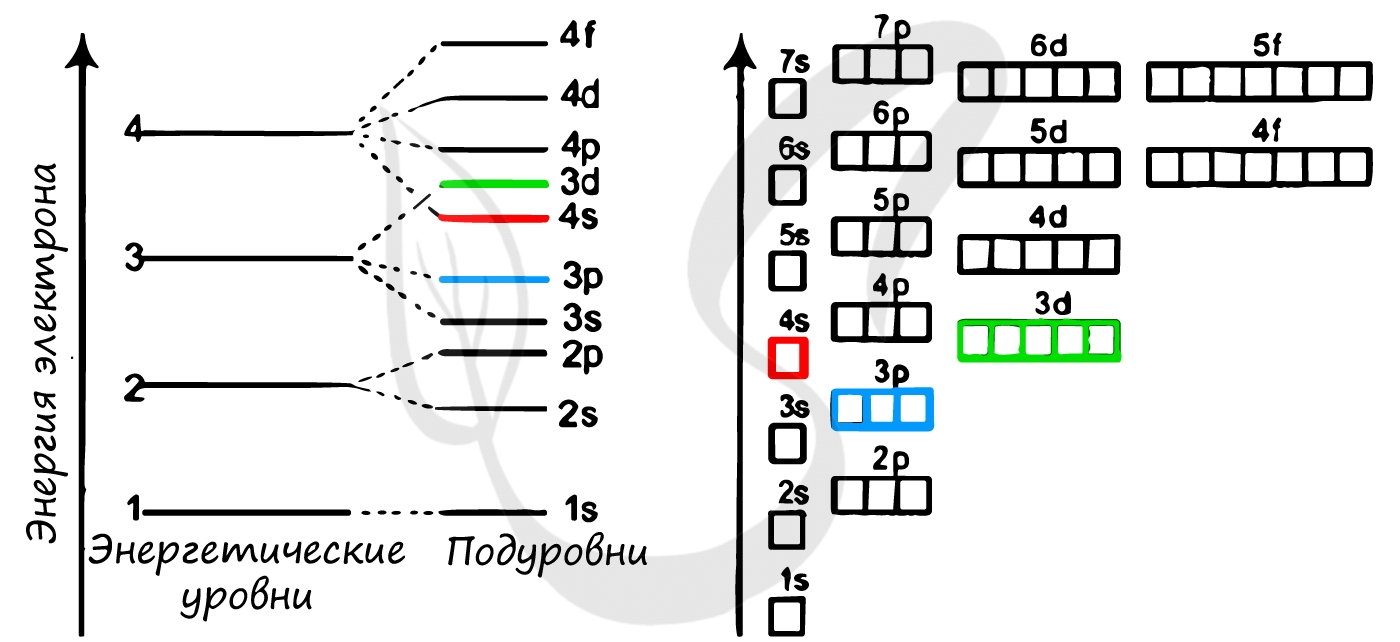
Должно быть, вы обратили внимание на некоторое несоответствие: после 3p подуровня следует переход к 4s, хотя логично было бы заполнить до конца 4s подуровень. Однако природа распорядилась иначе.
Запомните, что, только заполнив 4s подуровень двумя электронами, можно переходить к 3d подуровню.
Теперь мы располагаем указанное количество электронов на энергетических уровнях, руководствуясь правилами заполнения.
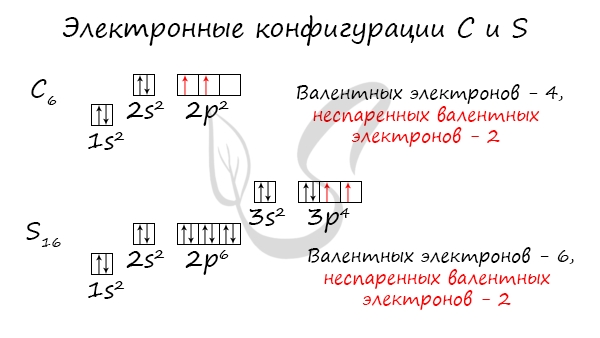
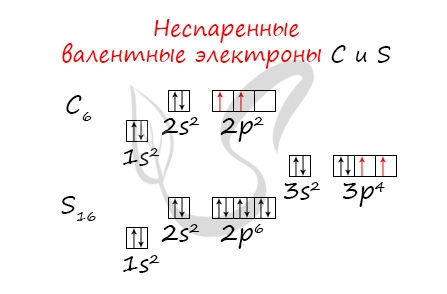
Обращаю ваше особе внимание: на 2p-подуровне углерода мы расположили 2 электрона в разные ячейки, следуя одному из правил. А на 3p-подуровне у серы электронов оказалось много, поэтому сначала мы расположили 3 электрона по отдельным ячейкам, а оставшимся одним электроном дополнили первую ячейку.
Внешний уровень и валентные электроны
Тренировка
Потренируйтесь и сами составьте электронную конфигурацию для магния и скандия. Определите число электронов на внешнем (валентном) уровне и число неспаренных электронов. Ниже будет дано наглядное объяснение этой задаче.
Что определяет энергетическое состояние электрона в атоме
Для лучшего понимания последнего утверждения рассмотрим упрощенную модель атома, «одномерный атом», в котором электрон может совершать лишь колебательные движения между крайними точками.
Будем считать также, что границы атома непроницаемы для электрона, так что он может находиться только внутри атома. Мы уже знаем, что состояние электрона в атоме характеризуется некоторой волной («волна де Бройля»). Но было бы неправильно представлять себе распространение этой волны как нечто подобное движению волны, образовавшейся на поверхности воды от брошенного камня: водяная волна неограниченно удаляется от места своего образования и постепенно расплывается, она не обладает устойчивостью во времени, тогда как электрон в атоме устойчив. Поэтому более правильной будет аналогия между состоянием электрона в атоме и состоянием звучащей струны, на которой образуются так называемые стоячие волны.
На рис. 6 схематически изображены стоячие волны, возникающие на колеблющейся струне, крайние точки которой закреплены. В точках, обозначенных буквой n, возникают пучности — здесь амплитуда колебания максимальна, в точках у струна не колеблется — это узлы, в которых амплитуда колебания равна нулю; в точках, расположенных между узлами и пучностями, амплитуда колебания имеет промежуточные значения. Поскольку конечные точки струны закреплены, здесь обязательно возникают узлы. В отличие от обычной «бегущей» волны, стоячая волна не перемещается в пространстве и не переносит энергии, которая лишь передается от одних точек струны к другим. Нетрудно видеть (рис. 6), что на струне с закрепленными концами длина стоячей волны может быть не любой, а только такой, чтобы на всей струне укладывалось целое число полуволн: одна (рис. 6, а), две (рис. 6,б), три (рис. 6, в) и т. д.
В рассматриваемой одномерной модели атома волна де Бройля тоже должна быть стоячей: это следует из того, что выйти за границы атома электрон не может и, следовательно, на границах атома волновая функция 
(т. е. амплитуда волны) должна обращаться в нуль. Поэтому рис. 6 может рассматриваться как модель одномерного атома со стоячими волнами де Бройля, которые могут в этом атоме образоваться.
Если длина одномерного атома равна l, то для случаев а, б и в на рис. 6 длина волны де Бройля будет выражаться следующим образом:
Следовательно, стоячая волна может образоваться только при условии
где 
, т. е. целое число.
Рис. 6. Стоячие волны на струне.
С другой стороны, согласно уравнению де Бройля
Приравнивая правые части двух последних уравнений, получим для скорости электрона 
выражение:
Теперь, зная скорость электрона 
, можно найти его кинетическую энергию Е:
Поскольку n — целое число, то последнее выражение показывает, что энергия электрона в одномерном атоме не может иметь произвольные значения: при n=1 она равна величине дроби 
, при n=2 она в 4 раза больше, при n=3 — в 9 раз больше и т. д. Таким образом, в случае одномерного атома волновые свойства электрона, выражаемые уравнением де Бройля, действительно имеют следствием квантованность энергетических состояний электрона. При этом допустимые уровни энергии электрона определяются значением целого числа n, получившего название квантового числа.
Разумеется, найденное выражение для энергии электрона относится к упрощенной модели атома. Но и для реального атома решение уравнения Шредингера также приводит к выводу о квантованности энергетических состояний электрона в атоме.
Модель одномерного атома позволяет понять, почему электрон, находящийся в атоме в стационарном состоянии, не излучает электромагнитной энергии (второй постулат теории Бора). Согласно модели Бора-Резерфорда, электрон в атоме совершал непрерывное движение с ускорением, т. е. все время менял свое состояние; в соответствии с требованиями электродинамики, он должен при этом излучать энергию. В одномерной модели атома стационарное состояние характеризуется образованием стоячей волны де Бройля; пока длина этой волны сохраняется постоянной, остается неизменным и состояние электрона, так что никакого излучения происходить не должно.
Становится ясным и вопрос о состоянии электрона при переходе из одного стационарного состояния в другое (в терминологии Бора — с одной стационарной орбиты на другую). Если, например, электрон из состояния, отвечающего рис. 6, а, переходит в состояние, соответствующее рис. 6,б, то во время этого перехода длина волны де Бройля будет иметь переменное значение, не отвечающее условию образования стоячей волны. Именно поэтому состояние электрона в этот промежуток времени будет неустойчивым; оно будет меняться до тех пор, пока длина волны де Бройля не будет вновь соответствовать условию образования стоячей волны, т. е. пока электрон не окажется в новом стационарном состоянии.
В упрощенной одномерной модели атома положение электрона относительно ядра определяется одной координатой, а его состояние— значением одного квантового числа. В двумерной (плоской) модели атома положение электрона определяется двумя координатами; в соответствии с этим, его состояние характеризуется значениями двух квантовых чисел. Аналогично в трехмерной (объемной) модели атома состояние электрона определяется значениями трех квантовых чисел. Наконец, изучение свойств электронов, входящих в состав реальных атомов, показало, что электрон обладает еще одной квантованной физической характеристикой (так называемый спин, см. § 30), не связанной с пространственным положением электрона. Таким образом, для полного описания состояния электрона в реальном атоме необходимо указать значения четырех квантовых чисел.
28. Главное квантовое число. Итак, в одномерной модели атома энергия электрона может принимать только определенные значения, иначе говоря — она квантована. Энергия электрона в реальном атоме также величина квантованная. Возможные энергетические состояния электрона в атоме определяются величиной главного квантового числа n, которое может принимать положительные целочисленные значения: 1, 2. и т. д. Наименьшей энергией электрон обладает при n=1 с увеличением n энергия электрона возрастает. Поэтому состояние электрона, характеризующееся определенным значением главного квантового числа, принято называть энергетическим уровнем электрона в атоме: при n=1 электрон находится на первом энергетическом уровне, при n=2 — на втором и т. д.
Главное квантовое число определяет и размеры электронного облака. Для того чтобы увеличить размеры электронного облака, нужно часть его удалить на большее расстояние от ядра. Этому препятствуют силы электростатического притяжения электрона к ядру, преодоление которых требует затраты энергии. Поэтому большим размерам электронного облака соответствует более высокая энергия электрона в атоме и, следовательно, большее значение главного квантового числа n. Электроны же, характеризующиеся одним и тем же значением главного квантового числа, образуют в атоме электронные облака приблизительно одинаковых размеров; поэтому можно говорить о существовании в атоме электронных слоев или электронных оболочек, отвечающих определенным значениям главного квантового числа.
Для энергетических уровней электрона в атоме (т. е. для электронных слоев, или оболочек), соответствующих различным значениям n, приняты следующие буквенные обозначения:
Что определяет энергетическое состояние электрона в атоме
Электронная оболочка атома и спектры
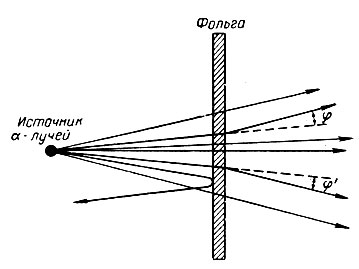
Рис. 2. Рассеивание α-лучей при прохождении через металлическую фольгу
Эрнест Резерфорд (1871-1937)
Так как, по мнению Резерфорда, атом является системой электронейтральной, то естественным оказалось утверждение, что положительное ядро окружено движущимися электронами, число которых равно заряду ядра или порядковому номеру. Совокупность всех электронов, окружающих данное ядро, получила название электронной оболочки атома.
Планетарная модель атома сыграла важную роль в начальной стадии изучения строения атома. Однако ряд вопросов оставался нерешенным. Например: Изменяется ли во времени энергия движущегося вокруг ядра электрона? На каких расстояниях от ядра движется электрон? Как объяснить линейный спектр атомов элементов?
Нильс Бор (1885-1962)
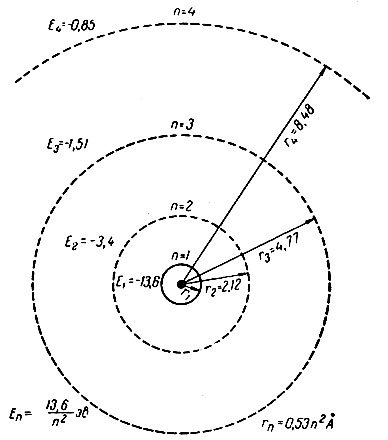
Рис. 3. Энергия электрона атома водорода в нормальном и возбужденном состояниях (по Бору)
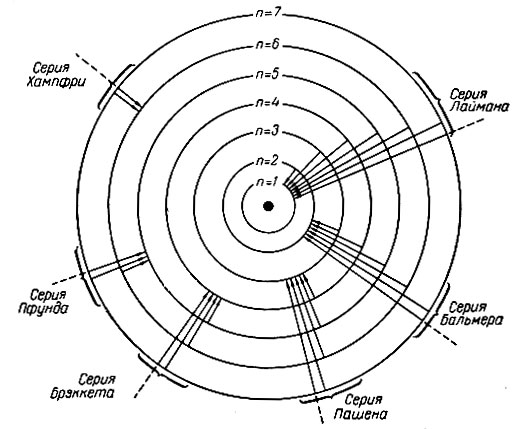
Рис. 4. Схема возникновения спектральных серий оптического спектра водорода
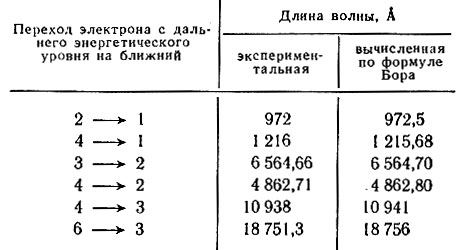
Таблица 19. Длины некоторых волн в оптическом спектре водорода
Впоследствии оказалось, что для характеристики электрона в атоме недостаточно знать только одно главное квантовое число n. Изучение тонкой структуры спектральных линий, расщепление их на составные компоненты под влиянием электрического и магнитного полей и наличие собственного момента движения электрона или спина (вращение вокруг собственной оси) показали, что для оценки состояния электрона в атоме необходимо пользоваться четырьмя квантовыми числами: n, l, m и s.
Зная порядковый номер элемента, т. е. заряд ядра его атома, а следовательно, и число электронов в атоме, можно проследить распределение этих электронов по энергетическим уровням и подуровням. Суммарная запись распределения максимального числа электронов в атоме по уровням 1, 2, 3 и 4 и возможным подуровням имеет вид:
Например, 12 электронов в оболочке атома магния (Z = 12) следующим образом распределятся по уровням и подуровням:
Из схемы и записи распределения видно, что в атоме магния три энергетических уровня и на внешнем из них содержится два s-электрона.
«В атоме не может быть двух электронов, обладающих одинаковыми значениями всех четырех квантовых чисел».
Следовательно, каждые два электрона, даже если у них одинаковые n, l и m, должны различаться значениями s. Например, со значениями n = 1, l = 0 и m = 0 может быть только два электрона, располагающиеся на одной орбитали и, следовательно, различающиеся спиновым квантовым числом s:
В атомной орбитали могут находиться:
либо одиночные (или непарные) электроны 
либо парные электроны с антипараллельными спинами 
В последнем случае суммарный спин электронов равен нулю 
Атомные орбитали, подуровни и уровни с суммарным значением спина, равным нулю, называются замкнутыми. Суммарный электронный спин атома в целом определяется лишь наличием одиночных, или непарных, электронов.
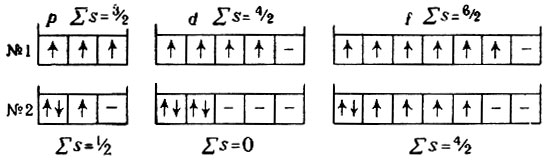
Как видно, в комбинации распределения № 1 занято большее число атомных орбиталей и суммарный спин электронов 
«В данном подуровне электроны должны занять по возможности все свободные орбитали, так как при этом суммарный спин электронов достигает наибольшего значения».
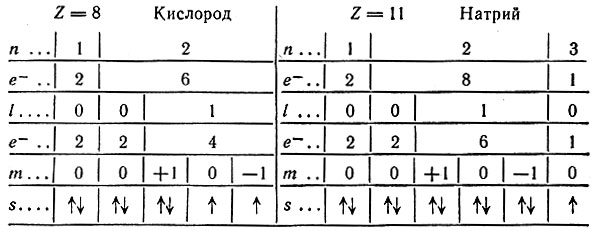
Этому правилу отвечает только комбинация № 1. В качестве примера рассмотрим строение атомов кислорода и натрия. На основании всего сказанного возможны только такие схемы распределения электронов в оболочке:
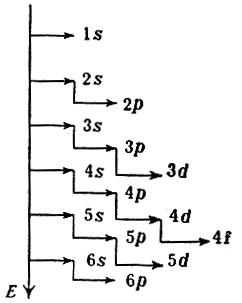
Таким образом, атомы имеют как бы слоистую структуру, и аналогичные внутренние уровни у атомов всех элементов построены одинаково. Однако чем больше Z, тем сложнее становится закономерность, определяющая последовательность заполнения электронами энергетических подуровней в атоме. Общим является только то, что электрон стремится занять подуровень энергетически более выгодный (наиболее низкий). Именно поэтому 19-й электрон атома калия располагается не на 3d-подуровне, а на 4s. Точно также подуровень 5s заполняется раньше, чем 4d, а подуровень 5р раньше подуровня 4f. Условно энергетические подуровни в атоме можно представить по их величине и порядку заполнения следующим образом:
Наиболее существенную роль в раскрытии тайн строения атома сыграл метод спектрального анализа. Следует различать оптические и рентгеновские спектры.
Оптический спектр является отображением всех возможных «незапрещенных» переходов электрона из возбужденных состояний в менее возбужденные или в основное состояния (внешний уровень). Оптические спектры очень сложны. Они состоят из десятков, сотен и тысяч спектральных линий.
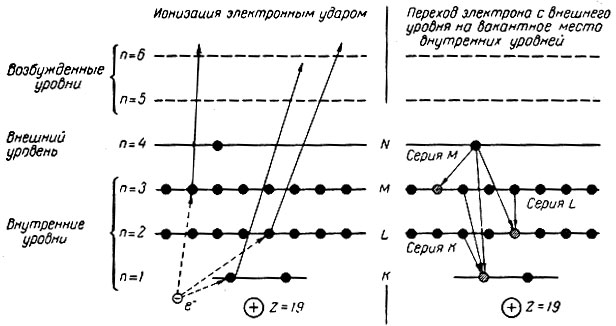
Рентгеновский спектр возникает при переходе электронов на вакантное место внутренних электронных уровней, образовавшееся в результате возбуждения атома вследствие соударения с электроном или фотоном (электронный или фотонный удар) при рентгеновском облучении. Если электроны перемещаются на самый близкий к ядру внутренний слой, то возникает серия К рентгеновского спектра; при переходах на иные внутренние слои появляются другие серии (рис. 5). Для самых сложных атомов известны семь серий рентгеновского спектра K, L, M, N, О, Р, и Q, отвечающих семи энергетическим уровням в электронной оболочке атома.
Рис. 5. Схема возникновения рентгеновского спектра калия (Z = 19; 1s 2 2s 2 2p 6 3s 2 3p 6 3d 0 4s 1
От оптических спектров рентгеновские спектры отличаются небольшим числом линий, например, в серии К всего пять линий.
В спектроскопии энергию электрона принято выражать определенным термом (T), который находят делением энергии (E), выраженной в эргах, на скорость света (с) и постоянную Планка (h), т. е. Т = E/ch.
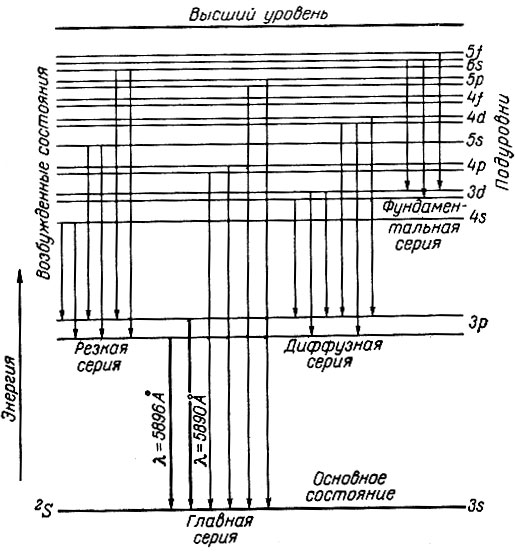
Аналогично рентгеновскому спектру важнейшие линии в оптическом спектре группируются в серии: главную, резкую, диффузную и фундаментальную (основную). Спектральные линии названных серий образуются при следующих переходах электронов:
Рис. 6. Схема возникновения оптического спектра натрия
* ( Объем этой книги не позволяет детально анализировать явление мультиплетности. Здесь рассматриваются лишь некоторые общие положения.)
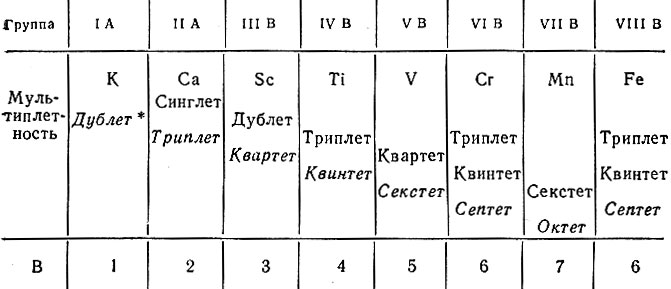
Периодичность в изменении свойств элементов получила объяснение не только на основе закономерного изменения структуры электронной оболочки атомов, но и на основе периодического изменения мультиплетности термов. При движении по периоду слева направо в системе элементов мультиплетность возрастает с попеременным чередованием четности (дублет, квартет, секстет, октет) и нечетности (синглет, триплет, квинтет, септет). В спектрах испускания, полученных в пламени электрической дуги (дуговые спектры), для элементов, атомы которых имеют нечетное число электронов, наблюдается четная мультиплетность, и наоборот (табл. 20).
Таблица 20. Изменение мультиплетности и характеристичной валентности у элементов начала четвертого периода
* ( Курсивом набраны термы, которые отвечают характеристичной валентности (В) элементов.)
Для основного состояния атомов элементов 2-го периода в зависимости от числа эквивалентных s- и p-электронов (эквивалентными называются электроны с одинаковыми значениями квантовых чисел n и l) термы обозначаются так:
Основной терм атомов d-элементов зависит от суммарного числа эквивалентных s- и d-электронов 
Причина многообразия валентности элементов объясняется различной мультиплетностью термов одного и того же элемента. Так как термы высокой мультиплетности (септеты, октеты, нонеты) проявляются редко, то и высшая валентность наблюдается относительно редко.