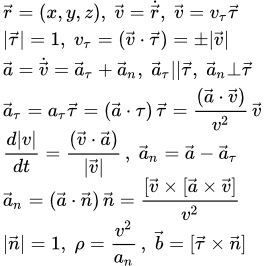Что необходимо знать при векторном способе задания движения точки
iSopromat.ru
Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.
Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.
В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.
Векторный
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
Координатный
При координатном способе задания движения задаются координаты точки как функции времени:
Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.
Естественный
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Теоретическая механика
16. Кинематика точки. Способы задания движения точки (векторный и координатный)
Кинематика изучает простейшую форму движения – механическое движение. Кинематически определить движение тела – это значит указать его положение относительно выбранной системы отсчета в каждый момент времени.
Движение материальной точки (в дальнейшем будем говорить просто точки) задано, если известен закон движения.
Закон движения. Закон движения – это уравнение, позволяющее определить положение точки относительно выбранной системы отсчета в любой момент времени.
Основная задача кинематики точки. По известному закону движения определить траекторию движения точки, ее положение на траектории, скорость и ускорение точки в ее положении на траектории.
Способы задания движения точки
В зависимости от выбора системы отсчета существуют три способа задания движения точки – векторный, координатный и естественный. Рассмотрим эти способы задания движения в отдельности.
Векторный способ задания движения точки
Таким образом, вектор 
определяет положение движущейся точки в любой момент времени. Следовательно, уравнение является законом движения при векторном способе задания движения.
Величина 
называется вектором скорости точки. Вектор скорости точки всегда направлен по касательной к годографу (траектории движения точки) в сторону перемещения точки.
Величина 
называется вектором ускорения точки.
Как показано на рис.К.10, вектор 
направлен в сторону вогнутости траектории движения точки, следовательно и вектор ускорения 
всегда направлен в ту же сторону, то есть в сторону вогнутости траектории движения точки.
Координатный способ задания движения точки
Компоненты скорости и ускорения движущейся точки в любой момент времени определяются по формулам
Модули скорости и ускорения 
Кинематика. Задание положения точки.
Положение точки в пространстве можно задать двумя способами: координатным и векторным.
При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:
Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).
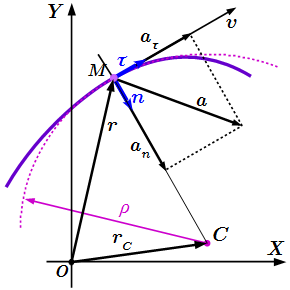
Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор 
Этот вектор называется радиус-вектором точки М.
Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.
Когда точка М движется, радиус-вектор 
непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени 
Зная эту функцию, для каждого времени t можно построить вектор 
и тем самым найти положение движущейся точки в данный момент. Функция 
называется векторным законом (векторным уравнением) движения точки М.
Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций rx, ry, rz на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:
Здесь за 
мы принимаем модуль радиус-вектора 
, а rx и ry являются его проекциями на оси координат, все три величины скалярны, x и y – координаты точки А.
Из этих уравнений видно, что между координатным и векторным способами задания положения точки существует связь.
Векторный способ задания движения точки
Введение
Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.
Основные формулы при векторном способе задания движения
Скорость точки
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.
Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.
Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.
Скорость и ускорение точки M при векторном способе задания движения
Единичный вектор в направлении касательной к траектории:
.
Ускорение точки
Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.
Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.
Тангенциальное ускорение
Нормальное ускорение
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Способы описания движения. Векторный способ. Координатный способ
По этой ссылке вы найдёте полный курс лекций по математике:
кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси. Рис. 1 Рис. 2 1.
Векторный способ. В этом способе положение материальной точки А задаётся с помощью так называемого радиус-вектора г, который представляет совой вектор, проведённый из точки О, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку А (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени г = r(t).
Геометрическое место концов радиус-вектора г (t) называют траекторией точки А. В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка А после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени At тело (точка А) переместилось из начального положения 1 с радиус-вектором Т\ в конечное положение 2 с радиус-вектором Т\ (рис. 2). Приращение А г радиус-вектора тела в таком случае равно: Вектор Аг, соединяющий начальное и конечное положения тела, называют перемещением тела. Отношение Аг/At называют средней скоростью (средним вектором скорости) vcp тела за время At: Способы описания движения.
Векторный способ. Координатный способ. Естественный (или траекторный) способ Вектор vcp колли неарен и сонаправлен с вектором Аг, так как отличается от последнего лишь скалярным неотрицательным множителем 1 / Аг. Предложенное определение средней скорости справедливо для любых значений At, кроме Д/ = 0. Однако ничто не мешает брать промежуток времени At сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени t или в конкретной точке траектории. С этой целью промежуток времени At устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение Аг. При этом отношение А/ / At стремится к определённому значению, не зависящему от At. Величина, к которой стремится отношение Аг / At при стремлении At к нулю, называется мгновенной скоростью v: Теперь заметим, что чем меньше At, тем ближе направление Аг к направлению касательной к траектории в данной точке.
Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела. В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости v тела (материальной точки). Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения.
Его определяют через отношение приращения вектора скорости Av тела к промежутку времени А/, в течение которого это приращение произошло.
Возможно вам будут полезны данные страницы:
Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (м/с) и метр на секунду в квадрате (м/с2 2. Координатный способ. В этом способе положение материальной точки А на плоскости в произвольный момент времени t определяется двумя координатами хну, которые представляют собой проекции радиус-вектора г тела на оси Ох и Оу соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями V= y(t).
| Если эти функции известны |
то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости v можно спроецировать на оси координат и определить таким образом скорости i\ и v.. изменения координат тела (рис. 4). В самом деле, vx и vy будут равны значениям, к которым стремятся соответственно отношения Ах/А t и Ay/At при стремлении к нулю промежутка времени At. Аналогично с помощью проецирования вектора а определяются ускорения ах и ах тела по направлениям координатных осей.
Само слово «средняя» означает усреднение по времени. Пример 1. Городской троллейбус утром вышел на маршрут, а через 8 часов, проехав в общей сложности 72 км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость vcp и средняя путевая скорость г>ср троллейбуса? Способы описания движения.
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.