Что измеряет палетка в физике

Математика. 4 класс

Конспект урока

Математика, 4 класс

Урок №14. Измерение площади фигуры с помощью палетки

Перечень вопросов, рассматриваемых в теме:

Площадь геометрической фигуры.

Вычисление площади фигур произвольной формы, используя палетку.

Основная и дополнительная литература по теме урока:

Теоретический материал для самостоятельного изучения

Вычислите площадь прямоугольника, если известно, что его длина равна 8см, а ширина 5см.

Вы уже знаете, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. S= 8 ∙ 5 = 40 см 2

А теперь попробуйте вычислить площадь данной фигуры:

-?

Чтобы найти площадь данной фигуры, нужно:

1) На данную фигуру наложить палетку. Не сдвигать!

3) Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.

4) Количество нецелых квадратных единиц разделить на 2, примерно столько целых квадратных единиц они образуют.

5) Сложить числа, полученные в пунктах 2 и 4.

6) В ответе записать, что площадь фигуры приблизительно равна найденной сумме.

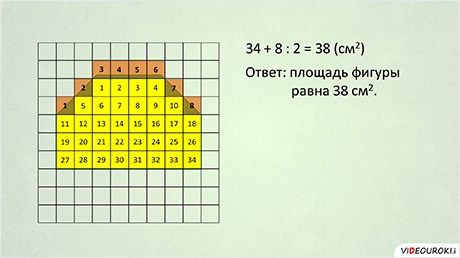
S = 34 + (8 : 2) = 38 см 2

Задания тренировочного модуля:

Правильный ответ: Прямоугольник – большую, круг – меньшую.

Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.

Источник

Измерение площади фигуры с помощью палетки

В школе дети знакомятся с большим количеством измерительных приборов и приспособлений.
Инна СЫЧЕВА, учитель школы № 1936 г. Москвы, показывает, как вычисляется площадь фигуры с помощью одного из таких приспособлений – палетки.

Тема. «Измерение площади фигуры с помощью палетки».

Цели. Научить выполнять приближенное вычисление площадей; познакомить с вычислением площади с помощью палетки по алгоритму; повторить единицы длины и единицы измерения площади; развивать мышление, внимание, память.

Оборудование. Учебник «Математика» (4-й класс, часть 1, авт. М.И. Моро и др.), таблица алгоритма, палетки, индивидуальные карточки, экран, эпидиаскоп, пленки с фигурами.

I. Организационный момент

II. Сообщение темы урока

Учитель. Сегодня на уроке вы научитесь выполнять приближенное вычисление площади и познакомитесь с приспособлением для этого.

III. Знакомство с новым материалом

У. Рассмотрите фигуру на экране.

– Сколько места занимает фигура А на плоскости? Другими словами, какова ее площадь?

Выслушиваются ответы детей.

– Ответ на этот вопрос мы можем дать лишь приблизительно, указав границы, в которых находится площадь фигуры А. Площадь фигуры больше 6 клеток, но меньше 16.

– Как мы будем рассуждать, чтобы вычислить площадь данной фигуры? Внутри фигуры А расположены 6 целых клеток, а остальные 10 клеток входят в нее частично: иногда меньшая часть клеток, а иногда – боRльшая. Поэтому всего в фигуре А содержится примерно.

6 + 10 : 2 = 6 + 5 = 11 ед.

Результат записывают на доске с помощью знака приближенного равенства ».

– Значит, площадь нашей фигуры приблизительно 11 квадратных единиц.

– Читать следует так: «Площадь приблизительно равна 11 квадратным единицам».

Все это мы смогли вычислить благодаря тому, что фигура А была разбита на клетки. Что делать, если таких клеток нет?

Дети. Самим расчертить фигуру на квадраты.

У. Правильно, но на это уйдет много времени. Чтобы ускорить работу, люди придумали приспособление для определения площади фигур.

Учитель раздает детям прозрачные пленки, расчерченные на квадратные сантиметры, и карточки с фигурами.

– Перед вами такое приспособление. Откройте учебники на странице 49 и прочитайте, как оно называется.

Д. Для приблизительного определения площади фигуры используется палетка.

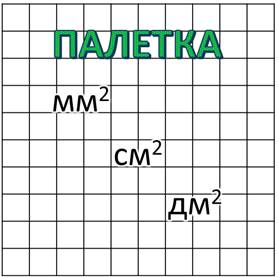
Палетка – прозрачная пленка, разделенная на одинаковые квадраты: это могут быть квадратные дециметры, квадратные сантиметры, квадратные миллиметры.

У. Посмотрите на ваши палетки. Как они разделены?

Д. На квадратные сантиметры.

У. В учебнике на странице 49 на цветные фигуры так же наложена палетка, разделенная на квадратные сантиметры. Прочитайте, как находили площадь фигуры голубого цвета.

Дети читают текст, отмеченный красной чертой.

– Чему равна площадь этой фигуры?

Д. Примерно 31 квадратный сантиметр.

У. Попробуем вывести формулу, по которой приблизительно считается площадь.

Дети вместе с учителем выводят и записывают формулу.

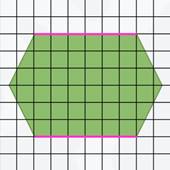
– Найдите площадь фигур зеленого и розового цветов.

Д. Площадь зеленой фигуры приблизительно равна 6 + 16 : 2 = 14 квадратных сантиметров.

– Площадь розовой фигуры приблизительно равна 5 + 16 : 2 = 13 квадратных сантиметров.

У. Возьмите в руки карточки с изображенными на них фигурами. С помощью палетки найдите их площадь.

Дети выполняют задание.

– Попробуем вывести алгоритм нахождения площади фигуры с помощью палетки.

Учитель записывает каждый шаг на доске.

1. Наложить палетку на фигуру.
2. Сосчитать число а целых клеток внутри фигуры.
3. Сосчитать число b клеток, входящих в фигуру частично.
4. Сосчитать приближенное значение площади.
S » a + в : 2 (если число b нечетное, то увеличить или уменьшить его на 1).

IV. Физкультминутка

V. Практическая работа

У. Нарисуйте на листе бумаги какую-нибудь замкнутую линию и найдите площадь фигуры, ограниченной этой линией.

Дети выполняют задание в тетради, находят площадь, называют свои ответы.

– Начертите циркулем окружность радиусом 4 сантиметра, найдите с помощью палетки площадь получившегося круга.

Дети находят площадь.

VI. Закрепление пройденного материала

У. Найдите задание 265 на странице 50. Задание выполняем по вариантам: вариант 1 – первая часть номера, вариант 2 – вторая часть.

Дети самостоятельно выполняют задание.

– Поменяйтесь тетрадями и проверьте работу ваших соседей.

Дети делают проверку.

– Вычислите периметр и площадь многоугольника.

Ученики выполняют задание по вариантам: вариант 1 – находят периметр, вариант 2 – находят площадь.

Р = 16 +15 +21 + 9 +7 + 36
Р = 104 дм
S =15 х 16 + 21 х 9
S = 429 дм 2

– Решите логическую задачу. Для каждой фигуры объясните, почему она лишняя.

Д. Сначала уберем фигуру В, так как среди четырехугольников – треугольник. Затем уберем фигуру С, так как останутся фигуры с попарно равными сторонами. Уберем фигуру D, так как в ней углы не прямые.

VII. Самостоятельная работа

У. Выполните упражнения 267 и 262.

Дети выполняют работу и сдают тетради.

VIII. Итог урока

У. С помощью какого инструмента вы научились находить приближенное значение площади фигуры?

Д. С помощью палетки.

У. Какой формулой вы пользовались?

У. Кто из вас научился выполнять приближенное вычисление площади фигуры?

Дети поднимают руки.

IХ. Домашнее задание

Учитель раздает карточки с цифрой 5:

У. Дома вычислите площадь цифры и решите задачи 261 и 263.

Источник

Палетка. Измерение площади фигуры с помощью палетки

Урок 7. Математика 4 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Палетка. Измерение площади фигуры с помощью палетки»

Вы знаете, я хотела узнать площадь нашей страны, но мне это не сразу удалось сделать. Дело в том, что её границы имеют неправильную форму – это не прямоугольник, не квадрат, и даже не круг.

Я обратилась за помощью к нашей царице, и она рассказала мне, как находить площадь любой, самой искривлённой фигуры. Царица дала мне вот такое простое приспособление. Это прозрачная пластина или плёнка с разлиновкой в клеточку. Называется она – палетка. В зависимости от размера фигуры, площадь которой надо узнать, палетка может быть разделена на квадратные миллиметры, квадратные сантиметры или квадратные дециметры.

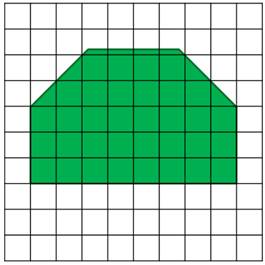
Представьте себе, что надо узнать площадь вот такой фигуры.

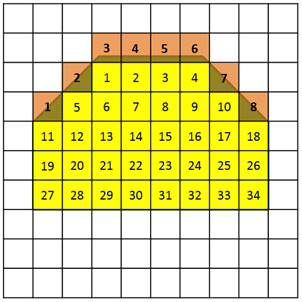
Накладываем на неё палетку.

Сначала считаем, сколько всего целых квадратиков. Их тридцать четыре. Теперь считаем все оставшиеся кусочки. Их восемь. Люди договорились, что каждые два кусочка засчитывают за один полный квадратик. Поэтому количество кусочков делим на два. Получилось четыре.

Складываем тридцать четыре и четыре. Это тридцать восемь. Значит, площадь этой фигуры – примерно тридцать восемь квадратиков.

Так как в школе чаще всего пользуются палетками, разделёнными на квадратные сантиметры, то вы бы сказали, что площадь данной фигуры примерно равна тридцати восьми квадратным сантиметрам. Почему примерно? Потому что площадь фигуры по палетке вряд ли возможно определить абсолютно точно, ведь редко два кусочка могут идеально заменить целый квадратик.

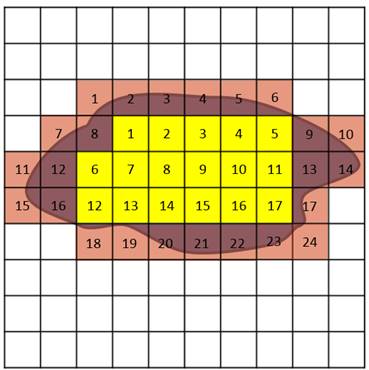
А теперь попробуем найти площадь вот такой, совершенно бесформенной фигуры.

Опять накладываем на неё палетку. Считаем целые квадратики.

Их семнадцать. Теперь считаем кусочки. Их двадцать четыре. Количество кусочков делим на два и полученное число прибавляем к семнадцати. Получилось примерно двадцать девять квадратных сантиметров.

Иногда случается и так, что количество кусочков – нечётное число, например, тринадцать или двадцать пять. Тогда делим на два ближайшее чётное число, больше данного на один. Ведь всё равно при помощи палетки точно площадь фигуры измерить невозможно. А вот почему берём чётное число больше данного, вы узнаете в пятом классе.

Запомнили, ребята, как мы определяем площадь фигур с помощью палетки?

̶ Накладываем палетку на фигуру.

̶ Считаем количество целых квадратов.

̶ Считаем количество кусочков.

̶ Количество кусочков делим на два…

̶ Складываем полученное число с количеством целых квадратов….

̶ Записываем ответ.

Кстати, именно так, используя план местности и палетку, можно найти площадь участка земли, или озера, или целого города, и даже страны. Вот этим я сейчас и займусь. Пока, ребята!

Источник

Палетка

См. также

Список значений слова или словосочетания со ссылками на соответствующие статьи. Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью.

Смотреть что такое «Палетка» в других словарях:

палетка — и, ж. palette f. пластинка, планка. 1. иск. В искусстве Древнего Египта каменная пластина для растирания красок. П. обтекаемой формы нередко вытачивались в виде гиппопотама, страуса, рыбы либо украшались высоким рельефом. В форме П. создавались… … Исторический словарь галлицизмов русского языка

палетка — пластинка, сетка, пленка Словарь русских синонимов. палетка сущ., кол во синонимов: 3 • пластинка (47) • … Словарь синонимов

ПАЛЕТКА — (от франц. palette пластинка планка), 1) прозрачная пластинка с нанесенной на нее сеткой линий (реже точек), предназначенная для вычисления площадей на планах и картах, отсчета координат и т. д.2) Тонкая каменная плитка с рельефными изображениями … Большой Энциклопедический словарь

ПАЛЕТКА — ПАЛЕТКА, палетки, жен. (франц. palette) (спец.). Прозрачная пластинка с нанесенной на нее сеткой квадратов, служащая для вычисления площадей на планах и картах, а также для вычерчивания по ним копий и схем. Толковый словарь Ушакова. Д.Н. Ушаков.… … Толковый словарь Ушакова

палетка — Нанесённая на прозрачной основе сетка квадратов определённых размеров, посредством которой определяется площадь участков на плане или карте; при помощи палетки осуществляется простейший графический способ численного интегрирования… … Справочник технического переводчика

палетка — Сетка параллельных или радиальных линий, квадратов, шестиугольников и других геометрических ячеек, нанесенная на прозрачный материал и используемая для измерений по географическим картам, планам, снимкам … Словарь по географии

палетка — и; мн. род. ток, дат. ткам; ж. [от франц. palette] 1. Спец. Сетка квадратов на прозрачной пластинке, бумаге, стекле и т.п. для определения площадей участков на планах и картах. Пользоваться палеткой. 2. Иск. Тонкая каменная плитка с рельефными… … Энциклопедический словарь

Палетка — (от франц. palette пластинка, планка) начерченная на прозрачной бумаге, стекле или целлулоидной пластинке сетка линий, образующих квадраты известных размеров, при помощи которых определяется площадь участков на плане или карте.… … Большая советская энциклопедия

Палетка — ж. Прозрачная пластинка с нанесенной на нее сеткой квадратов, служащая для вычисления площадей на планах и картах. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

Источник

Измерение площади фигуры с помощью палетки

Урок 20. Математика и игры 3–4 классы

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Измерение площади фигуры с помощью палетки»

В повседневной жизни людям часто приходится находить площадь комнаты, площадь окна в комнате, площадь садового участка, площадь поля.

Так, например, площадь комнаты надо знать, чтобы купить необходимое количество краски для покраски пола в этой комнате. Чтобы найти площадь комнаты, надо её длину умножить на ширину. Ведь пол комнаты обычно имеет форму прямоугольника.

Таким же образом можно найти площадь грядки в огороде, так как она представляет собой прямоугольник.

А вот как, например, найти площадь лужи? Ведь её границы имеют неправильную форму – это не прямоугольник, не квадрат и даже не круг.

Сейчас мы поговорим о том, как найти площадь любой, даже самой искривлённой фигуры.

Посмотрите на эту прозрачную пластинку или плёнку с разлиновкой в клеточку, которая называется палеткой. В зависимости от размера фигуры, площадь которой надо узнать, палетка может быть разделена на квадратные миллиметры, квадратные сантиметры, квадратные дециметры.

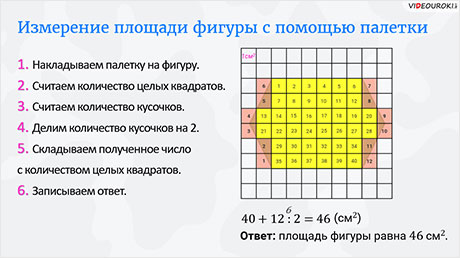
Давайте найдём площадь вот такой фигуры.

Итак, возьмём палетку, которая разделена на квадратные сантиметры. Следует отметить, что в школе чаще всего пользуются именно такими палетками.

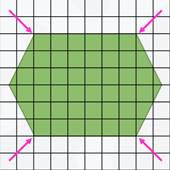
Накладываем эту палетку на нашу фигуру так, чтобы, если это возможно, хотя бы одна сторона совместилась с линией разлиновки палетки. У нашей фигуры удалось совместить даже не одну, а две стороны. И уголки верхней и нижней сторон фигуры совпадают с уголками клеточек палетки.

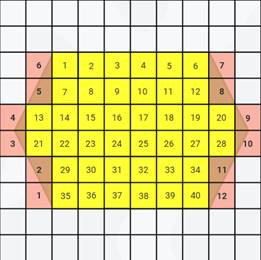
Сначала считаем, сколько всего целых квадратов, то есть квадратных сантиметров, укладывается в данной фигуре. Их 40.

Теперь считаем все оставшиеся кусочки. Их 12.

Каждые 2 таких кусочка принято засчитывать за 1 полный квадратик. Поэтому количество таких кусочков надо разделить на 2.

Далее к 40 прибавляем частное 12 и 2. Получаем 46. Так как палетка разделена на квадратные сантиметры, то площадь фигуры примерно равна 46 квадратным сантиметрам.

40 + 12 : 2 = 46 (см 2 )

Примерно, потому что с помощью палетки площадь фигуры вряд ли можно точно определить. Ведь 2 кусочка редко могут идеально заменить целый квадратик.

А сейчас давайте найдём с помощью палетки площадь вот такой фигуры.

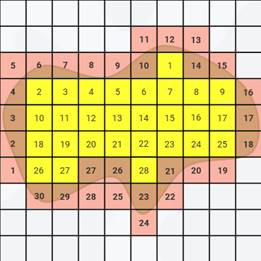
Эта фигура напоминает лужу и здесь уже совместить линии фигуры с разметкой палетки не получится. Снова воспользуемся палеткой, которая разделена на квадратные сантиметры. Накладываем её на данную фигуру и считаем целые квадратики. Их 28.

Теперь считаем кусочки. Их 30.

Снова повторим, что 2 таких кусочка принято засчитывать за один полный квадратик, поэтому их количество надо разделить на 2.

К 28 прибавим частное 30 и 2. Получим, что площадь рассматриваемой фигуры примерно равна 43 квадратным сантиметрам.

28 + 30 : 2 = 43 (см 2 )

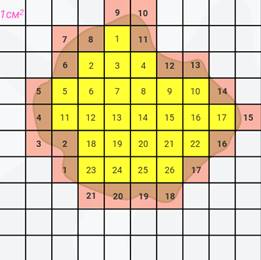
Далее найдём площадь вот такой фигуры.

Накладываем на неё палетку. В первую очередь считаем, сколько целых квадратиков укладывается в этой фигуре. Их 26. Теперь считаем кусочки. Их 21.

Обратите внимание, что в данном случае количество кусочков – нечётное число. В таком случае на 2 надо делить ближайшее чётное число, которое больше данного на один, ведь всё равно с помощью палетки точно найти площадь фигуры невозможно. А вот почему берём чётное число, которое больше данного, вы узнаете в пятом классе. То есть надо 22 разделить на 2.

Таким образом, чтобы найти площадь фигуры, к 26 прибавим частное 22 и 2. Получим, что площадь примерно равна 37 квадратным сантиметрам.

26 + 22 : 2 = 37 (см 2 )

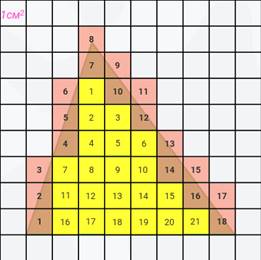
И найдём площадь ещё одной фигуры – треугольника.

Накладываем на него палетку. Здесь удаётся с разметкой палетки совместить одну из сторон. Я думаю, вы уже догадались, что если удастся совместить одну из сторон фигуры с разметкой палетки, и углы фигуры совместятся с уголками квадратиков, то останется меньше кусочков, и измерение будет более точным.

Сначала считаем целые квадратики. Их 21. Затем считаем кусочки. Их 18.

Прибавим к 21 частное 18 и 2 и получим, что площадь треугольника примерно равна 30 квадратным сантиметрам.

21 + 18 : 2 = 30 (см 2 )

Итак, повторим, как мы определяем площадь фигуры с помощью палетки.

Источник