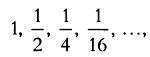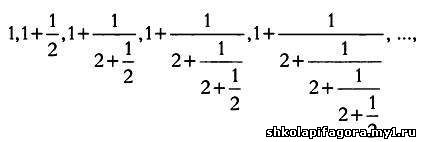Что значит эпсилон в математике
Что значит эпсилон в математике
Когда говорят об эпсилонах или о языке эпсилон-дельта, речь идет вовсе не о секретных кодах Министерства обороны, а о сложном математическом аппарате, который напрямую связан с понятием предела. Первое определение понятию предела сформулировал Бернард Больцано (1781–1848), не получивший, к сожалению, при жизни должного признания. Первым, кто использовал это понятие на практике, был Огюстен Луи Коши (1789–1857), однако окончательное строгое определение предела дал Карл Вейерштрасс. Определение предела на языке эпсилон-дельта является чрезвычайно точным в той части, которая касается делимости на бесконечное множество частей. Хотя это определение очень сложно понять тому, кто не владеет некоторыми математическими знаниями, оно тем не менее долгое время использовалось в учебниках для средней школы. Мы не хотим сказать, что старшеклассники недостаточно умны, чтобы понять его, но не стоит ожидать, что все поймут его с одинаковой легкостью. Во многих учебниках оно приводится мелким шрифтом, и преподаватели обходят его молчанием.
Карл Вейерштрасс на литографии 1895 года. Этот немецкий математик был первым, кто использовал на практике язык эпсилон-дельта.
Переписка, несомненно, является древнейшей формой общения между учеными. С ее помощью формулируется и решается множество задач. По сравнению с другими формами общения письма обладают преимуществом — конфиденциальностью: они адресуются конкретному человеку или группе людей. В виде переписки проходили многие научные дискуссии.
Одной из самых известных стало жаркое противостояние между Ньютоном и Лейбницем об авторстве математического анализа. Абсолютно независимо друг от друга они получили аналогичные результаты, однако Ньютон опубликовал свои работы первым, что дало ему основания обвинить Лейбница в плагиате. Это привело к ожесточенному и абсурдному спору, не имевшему аналогов в истории науки.
Попробуем сделать понятие предела более ясным, несколько упростив его.
По сути оно имеет много общего с понятием накопления. Представим, что перед входом в помещение образовалась очередь. Можно заметить, что люди постепенно становятся ближе ко входу и друг к другу. Это совершенно естественно: изначально, когда в очереди немного людей, они стараются сохранять комфортное расстояние между собой, но по мере того как число людей растет, расстояние между ними уменьшается. Интересно, что мы говорим о двух разных расстояниях, которые, однако, тесно связаны между собой: о расстоянии между началом очереди и входом и о расстоянии между людьми в очереди, которое по мере того как мы приближаемся к концу, увеличивается. Это логично, так как те, кто становится в очередь, стараются сохранять комфортное расстояние между собой, но по мере того как очередь движется вперед, люди чувствуют давление тех, кто находится позади. Можно сказать, что люди скапливаются у входа.
Можно определить степень скопления людей с помощью параметра, который будет описывать, например, изменение расстояния между людьми в очереди по мере приближения к ее началу. Как правило, этот параметр будет постепенно уменьшаться.
В очереди, например у входа в кинотеатр, люди собираются у дверей, где расстояние между ними будет минимальным. По мере отдаления от входа расстояние между людьми увеличивается.
Степень скопления людей можно определить, выбрав в качестве единицы измерения конкретное расстояние, например 50 см. Если в 50 см от входа находятся люди, это будет соответствовать определенной степени скопления. В зависимости от величины этой единицы измерения число людей будет изменяться. Аналогично можно измерить степень скопления людей, оценив расстояние между ними.
Здесь возникает первый интересный вопрос: когда мы видим скопление людей, логично предположить, что они собрались по какой-то причине, то есть это скопление возникает вокруг определенного места, где происходит что-то важное. Когда мы видим на дороге скопление муравьев, то сразу же понимаем, что где-то поблизости находится еда или вход в муравейник. Еще один пример — скопление машин на автомагистрали, которое служит признаком того, что поблизости находится пункт оплаты проезда или произошла авария. Эти примеры помогут нам понять одно из самых интересных открытий в истории математики. Оно касается существования определенных чисел, которые в течение веков скрывались в мире бесконечно малых.
В предыдущих примерах речь шла о дискретных множествах. Рассмотрим непрерывные величины, так как они допускают возможность бесконечного деления.
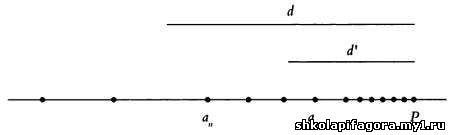
Оставим скопления людей и автомашин и рассмотрим возможные множества точек на прямой. Допустим, что дана последовательность точек а 1, a 2, а 3, а n…, которые обладают одним свойством: соседние члены последовательности располагаются все ближе и ближе друг к другу. Очевидно, что они скапливаются вокруг некоторой точки — обозначим ее Р. Допустим, что выбранной нами основной мерой длины является отрезок длиной d. Если мы поместим один конец этого отрезка в точку Р, то увидим, что некоторые точки последовательности окажутся внутри этого отрезка длиной d.
Более того, мы сможем найти точку а n, после которой все точки будут располагаться внутри отрезка d. Если мы уменьшим длину отрезка и сделаем ее равной d’ d, то все точки, начиная с более удаленной, а m, будут располагаться внутри этого нового отрезка. Именно такое значение имеет эпсилон в математическом анализе.
Мы можем гарантировать, что для любой величины d всегда найдется такое n, начиная с которого все элементы последовательности будут находиться внутри отрезка d. В этом случае говорят, что последовательность сходится в точке Р. Это означает следующее: во-первых, эта последовательность бесконечна, во-вторых, расстояние между точкой Р и произвольным членом последовательности может быть сколь угодно малым.
Когда мы работаем с дискретными множествами, все изложенное выше практически неприменимо. Рассмотрим последовательность чисел 100, 50, 25, 12, 6, 3, 1 (можно представить эту последовательность как очередь из семи чисел у входа, которым, например, является ноль). Очевидно, что разница между произвольным членом последовательности и нулем постепенно уменьшается, равно как и разница между двумя соседними членами последовательности. Например, между 100 и 50 находится 49 чисел, между 6 и 3 — всего два. Тем не менее нельзя сказать, что члены последовательности скапливаются в окрестности точки 0. Очевидно, что если мы возьмем отрезок длиной 1/2 и поместим один из его концов в точку 0, на этом отрезке не будет находиться ни один член последовательности. А если мы рассмотрим последовательность
то вблизи нуля всегда будет находиться какой-либо ее член, сколь бы малым ни было расстояние до нуля.
На языке математики эти расстояния называются окрестностями. Окрестность подобна скобкам, в которые заключена точка Р. Основная идея заключается в том, что сколь малыми ни были бы эти скобки (то есть радиус окрестности), в них всегда будут находиться элементы последовательности. В языке эпсилон-дельта основную роль играет соотношение между двумя числами: шириной скобок (радиусом окрестности, который обычно обозначают ε — эпсилон) и числом n, определяющим элемент а n, начиная с которого все элементы последовательности будут располагаться внутри заданной окрестности. На языке математики это звучит так: «Для любого эпсилон существует n, такое что…»
Именно так определяется понятие бесконечного деления, очень близкое к понятию предела. Когда в одном из парадоксов Зенона интервал делится пополам бесконечное число раз, мы формируем последовательность, подобную описанной в предыдущем примере. Теперь мы можем воспользоваться строгим определением перехода к пределу и подтвердить, что последним членом последовательности будет 0. Это не помогает разрешить парадокс, так как ситуация, по сути, не изменилась: точки образуют бесконечную последовательность и скапливаются вблизи нуля, и мы считаем, что существует последняя точка последовательности, 0, но в действительности 0 не является членом этой последовательности. Это утверждение не является оправданным, но четко определено на языке математики. Как говорил Бертран Рассел, «математика может быть определена как доктрина, в которой мы никогда не знаем ни о чем говорим, ни того, верно ли то, что мы говорим».
В действительности Коши в своем определении предела использовал не точки, которые скапливаются вокруг некоторой данной точки, а точки, которые скапливаются рядом друг с другом. Иными словами, скопление точек, которое рассматривал Коши, подобно скоплениям автомобилей на разных участках дороги, вызванным множеством аварий в разных местах. Ситуация значительно осложняется тем, что если мы рассматриваем исключительно рациональные числа, то прямая, на которой они располагаются, не будет заполнена — на ней останутся промежутки. Например: дана последовательность точек (теперь мы связываем точки на прямой с рациональными числами), которые скапливаются все плотнее и плотнее. Эту ситуацию можно четко определить на языке математики, что сделал Коши. Однако проблема заключается в том, что эти точки могут скапливаться вокруг пустого места на прямой, точнее вокруг точки, которой не соответствует никакое рациональное число.
Так происходит, например, в случае с последовательностью
о которой мы говорили в главе 2 и которая сходится к числу √2, а оно не является рациональным. Разумеется, мы можем построить прямоугольный треугольник, гипотенуза которого будет равна √2, но так мы определим это число геометрически, а во времена Коши математики пытались дать определение числам чисто арифметическими или аналитическими методами. Рациональные числа, по сути, вообще не были определены как числа, пока Дедекинд и, позднее, Кантор не сформулировали для них точной дефиниции. Последний сделал не только это, но и устранил промежутки на числовой прямой, которых в действительности существует бесконечное множество, так как иррациональных чисел, равно как и рациональных, бесконечно много.
Однако Кантор заслуживает отдельной главы, ведь он не только заполнил числовую прямую, устранив эти промежутки, но и первый встретился с бесконечностью лицом к лицу.
Что такое предел? Что такое |Xn-A| Математика Наука
Для начала успокойтесь, я понимаю на носу экзамен, но для математики нужна «холодная голова». Сейчас мы во всем разберемся, все очень просто на самом деле 🙂
Начнем с того, что вы немного запутались в обозначениях. Последовательность принято записывать в фигурных скобках:
Я допускаю, что иногда лектор (учитель) опускает фигурные скобки и обзывает последовательность просто Xn, и тут уже надо понимать из контекста, где речь идет о целой последовательности, а где о ее конкретном элементе (это не сложно, как правило).
Теперь, собственно, предел. Говорим о числовых последовательностях (для нечисловых все тоже самое, только слова другие). Так как нельзя брать предел от числа — это бессмыслица, то нет нужды писать фигурные скобки в пределе : lim
Запись, lim Xn = A, значит, что при стремлении n к бесконечности, то есть вы берете все больше и больше членов последовательности
Вот собственно и все! Теперь вы можете попробовать посмотреть, как работает это определение на простых последовательностях, например:
2)
Обратите внимание, в первом случае предел не принадлежит последовательности, а во втором — принадлежит.
что какой эпсилон
Ε, ε (название: э́псилон, греч. έψιλον) — 5-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 5. Происходит от финикийской буквы hé — hé. От буквы «эпсилон» произошли латинская E и кириллическая Е. Название «эпсилон» (греч. Ε ψιλόν — «е простое» ) было введено для того, чтобы отличать эту букву от созвучного сочетания αι.
Использование
Заглавная буква эпсилон в основном не используется как символ, поскольку пишется так же, как и заглавная латинская буква E.
В различных дисциплинах при помощи строчной буквы ε обозначаются:
в математическом анализе — положительное сколь угодно малое вещественное число; см. примеры в статье Предел последовательности;
в алгебре — предельное порядковое число последовательности \omega,\omega^<\omega>,\omega^<\omega^<\omega>>,\dots.
в теории множеств — отношение принадлежности элемента множеству (такое обозначение является устаревшим, сейчас для той же цели используется символ ∈);
в тензорном исчислении — символ Леви-Чивиты;
в теории автоматов — эпсилон-переход;
в физике — угловое ускорение; коэффициент экстинкции оптического поглощения; проводимость среды; электронный захват; относительное удлинение; диэлектрическая проницаемость среды; энергия активации; ЭДС; ε0 — универсальная электрическая постоянная.
в астрономии — пятая (как правило) по яркости звезда в созвездии;
в программировании — точность численного типа данных;
в информатике — пустая строка;
в фонетике — неогубленный гласный переднего ряда средне-нижнего подъёма.
в теории метаболического контроля — эластичность фермента
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Определение предела и число эпсилон
 |
1. Предел последовательности.
Цитирую:
2. Геометрический смысл того же предела последовательности:
Заранее благодарен за ответ.
| Заслуженный участник |
 |
| Заслуженный участник |
 |
Последний раз редактировалось ИСН 16.02.2013, 20:14, всего редактировалось 1 раз.
| Заслуженный участник |
 |
| Заслуженный участник |
|
| Заслуженный участник |
|
|
Последний раз редактировалось henehen 16.02.2013, 22:34, всего редактировалось 3 раз(а).
PS. Причём, что самое интересное, такая привычка «объяснять» через левые переменные навроде эпсилонов и дельт сохраняется практически во всех учебниках и методичках, что весьма здорово способствует механическому использованию математики (не вникая ни во что) и убивает напрочь желание учиться.
И вообще, если кто-то мне объяснит человеческим языком на пальцах всю эту эпсилон-дельту технику, то я буду нечеловечески ему благодарен =)
| Заслуженный участник |
|
|
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Что такое точность epsilon?
Напишите программу, которая оценивает значение математической константы e по формуле e*=*1*+*1/1!*+*1/2!*+*1/3!*+*. с заданной введенной точностью epsilon.
ну вот написал я прогу, Е у меня высчитывается, а что за ЭПСИЛОН? какона работает как ее задать? зачем она ваще нужна и где могла бы пригодиться?
Что такое файловый буфер? Что такое режим (модификатор) доступа, при работе с файлами?
Что такое файловый буфер? Что такое режим (модификатор) доступа, при работе с файлами?
Что такое IIS и что такое PWS? Почему одно без другого не работает?
вот уже второй день пытаюсь немного разобраться в АСП. накидал небольшую тестовую страничку. но с.
Что такое рекурсивный тип данных? Что такое конструкция рекурсивного типа?
Что такое рекурсивный тип данных? Что такое конструкция рекурсивного типа?
Что такое напряжение и что такое сила тока с позиции заряженных частиц
Объясните пожалуйста, что такое напряжение и что такое сила тока с позиции заряженных частиц.
пошарил значит на википедии, и вот что там нашел:
Упоминания о чем-то схожем попадаются в книжке Подбельского В. В. » Введение в программирование на языке си » 2004 года, которую можно откопать, например тут, в ней, на странице 83 приведен алгоритм «оценки машинного нуля», и сдается мне, что этот мышиный ноль именно то, что вам нужно. Если описать эту зверушку в коде, получится примерно так:
результат вывода странный, что я делаю не так?
Добавлено через 17 минут
например при EPSILON = 0.5 а X = 2 выдает INF в выводе
Добавлено через 36 минут
Только что заменил глупую ошибку в функции подсчета, вроде заработало, но прошу экспертной оценки
— очень плохой код. Прежде, чем программировать, нужно вывести рекуррентную формулу, которая связывает следующий член ряда с предыдущим:
Если что, мой пост был не с целью критики а анализ библиотечной реализации, вашей и SadiQ228‘а. Как ни странно, по эффективности методы не так уж сильно отличались. ну за исключением того, что вычисление факториала и степени с нуля давало громадную ошибку. Но это я еще перепроверю
Добавлено через 1 час 16 минут
Итак, результаты
библиотечный exp(): 0.040448 мкс
функция SadiQ228’а: 1.07945 мкс
функция Catstail’а: 0.142243 мкс
То есть способ с использованием предыдущего значения в 7,5 раз быстрее «лобового», но в 3,5 раза медленнее библиотечного (наверняка там пошаманили с оптимизациями). Если поставить epsilon = 1e-5 то результаты ближе:
exp(): 0.040998
SadiQ228’а: 0.814409
Catstail’а: 0.0630968
ребят, продолжая тему точности, пытаюсь высчитать E по другому ряду.
1/e = (-1)^n/n!; n=2
пытаюсь сделать но ответы удивляют, подскажите где ошибаюсь?
Решение
Легко. Просто надо вспомнить, что n! = n*(n-1)!
Добавлено через 8 минут
Типа того. А где ты здесь видишь факториалы? Хотя они, конечно, есть