Что необходимо знать чтобы правильно выполнить сложение или вычитание чисел
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
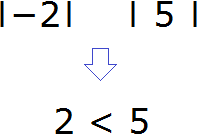
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Математика. 2 класс
Конспект урока
Математика, 2 класс. Урок №27
Проверка сложения. Проверка вычитания.
Перечень вопросов, рассматриваемых в теме:
— Что такое обратные математические действия?
— Как проверить сложение?
— Как проверить вычитание?
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых).
Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Обратные действия – действия, приводящие к прежнему, исходному состоянию.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
Теоретический материал для самостоятельного изучения
Используя числа 7, 5, 12 составим все возможные равенства.
Назовём компоненты и результат действия сложения.
Слагаемое + слагаемое = сумма
Назовём компоненты и результат действия вычитания.
Уменьшаемое – вычитаемое = разность
Действия сложение и вычитание связаны друг с другом, являются взаимно обратными действиями.
Как проверить, верно ли выполнено сложение. Воспользуемся знанием того, как связаны слагаемые и сумма. Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое. Это позволяет сложение проверить вычитанием.
Например, надо проверить, верно ли вычислили сумму чисел 28 и 5. Для этого из суммы 33 вычтем одно из слагаемых. Например, 5. Должно получиться другое слагаемое. Получилось 28. Значит, сумма чисел 28 и 5 найдена правильно. Можно вычесть из суммы другое слагаемое.
Сумма чисел 36 и 9 найдена неверно, т.к. после вычитания из суммы 47 слагаемого 9, другое слагаемое, 36 не получается.
Вычислим ещё раз сумму чисел 36 и 9 и проверим результат.
36 – первое слагаемое
Сформулируем правило проверки сложения: «Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно».
Как проверить вычитание? Воспользуемся знанием того, как связаны между собой уменьшаемое, вычитаемое, разность. Если к разности прибавить вычитаемое, то получится уменьшаемое. Значит, вычитание можно проверить сложением.
Вычислим разность чисел 48 и 30. Она равна 18. Проверим вычитание сложением. К разности 18 прибавим вычитаемое 30, получим 48. Это уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Значит, вычитание можно проверить и вычитанием. Рассмотрим это на примере.
Из уменьшаемого 48 вычтем разность 18, получим 30, т.е. вычитаемое. Значит, разность чисел 48 и 30 вычислена верно.
Сформулируем правила проверки вычитания: «Для проверки вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно», или «Для проверки вычитания, надо из уменьшаемого вычесть разность. Если в результате получается вычитаемое, значит, вычитание выполнено верно».
Вывод: Сложение и вычитание – это обратные действия. Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно. Для того, чтобы выполнить проверку вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно.
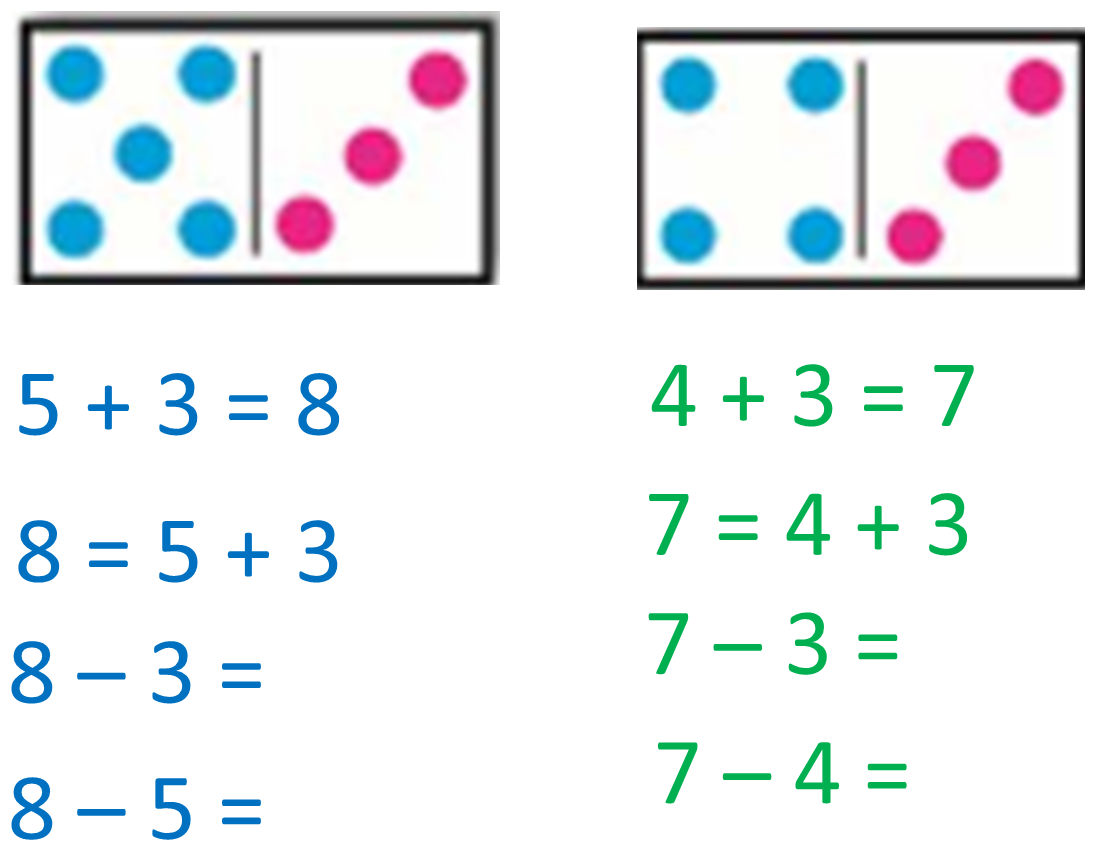
1. Найдите значение первого выражения в каждой рамке, а затем выполни проверку полученного результата двумя способами.
Сложение и вычитание целых чисел
В данном уроке мы изýчим сложение и вычитание целых чисел.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Рассмотрим следующее простейшее выражение
Значение данного выражения равно 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3
Значение данного выражения равно −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.
Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Можно воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками, потому что −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа, модуль которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3. Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:
После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) в ычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
Заменим вычитание сложением:
Дальнейшее вычисление не составляет труда:
Пример 7. Найти значение выражения −4 − 5
Приведём выражение к понятному виду:
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
Вычесть одно число из другого означает, прибавить к уменьшаемому такое число, которое противоположно вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Быстрое обучение детей счету примеров в пределах 10 и 20
Обучение будущего школьника счету в пределах 10 – это первый шаг к устному счету. Важно, чтобы ребенок запомнил процессы всех вычислений, как делают это старшие. Второй этап состоит из осваивания основных методов вычисления. Преимуществом здесь уже становится не произвольное получение из воспоминаний готовых ответов, а осознание и заучивание способов сложения и вычитания в цифрах. Как научить ребенка считать примеры в пределах 10, какие игровые приемы можно использовать для лучшего усвоения?
Учимся решать примеры до 10
Для того чтобы выучиться верно и мгновенно считать, нужно постоянно решать примеры. Для высчитывания и запоминания на начальных этапах следует сделать акцент на мышлении ребенка на основе наглядных образов. Здесь возникает проблема: дети часто не воспринимают математические понятия. Решением станут практические действия с жизненными примерами.
Учителя используют три основных метода для обучения счету:
Рассмотрим все методики по порядку.
Примеры на вычитание с картинками
Принцип знания состава
Подготовка должна начинаться с изучения азов математики. Рассказывая ребенку, нужно объяснять, что каждое число это группа с заданным количеством элементов.
Состав числа для запоминания
Важно! Мало сосчитать до пяти. Убедитесь, что вы предлагаете показать пять пальцев, положить на стол пять конфет или изобразить на листке пять кругов.
Необходимо связать число и сказочных героев или другие знакомые для ученика предметы:
Ребенка важно приучать к картинке, соединенной со всеми элементами. Необходимо играть в математическое домино. Для этого нужно взять десять кубиков с размером ребра 1,5-2 см, стоящих в коробке. Подойдут и детали конструктора Лего. Если нет подходящих предметов, то можно распечатать другие пособия.
Исходя из знания состава, ребенок может решить, складывать ему или вычитать. Например, чтобы ответить, сколько будет «шесть плюс три», он должен знать, что 6 и 3 равняются 9. А «семь минус два» получится пять, потому что 7 это 2 и 5.
Пособие для изучения состава
Запоминания таблиц наизусть
Есть большое количество приемов приучить ребенка сразу запомнить таблицы. Почти половина примеров на сложение и вычитание бессознательно заучиваются детьми по окончании ознакомления с законом перемещения.
Можно брать стихи, подпевки. Самым популярным образцом служит строка песни «Дважды два четыре, это всем известно в целом мире». Отличную информацию находят, познакомившись с методикой Николая Зайцева, программой «Песнезнайка».
Для закрепления знания табличных данных, можно предложить детям работать с:
Умение прибавлять в тестах со звездочкой поможет потом учить сложный материал.
Использование вычислительных приемов
Наивысший уровень результата устного счета – это способность нахождения самого быстрого и удобного метода для подсчета итога. Так, например, одним из легких способов обучить школьника считать на занятиях является техника присчитывания и «перепрыгивания». Дети быстро усваивают, что при добавлении 1 получается последующее значение, а при уменьшении на 1 получается предыдущее. После этого можно узнать о лучшем напарнике числа 2 – кузнечике, который умеет перескочить цифру и вызвать результат сложения или вычитания 2.
Как объяснить связь сложения и вычитания
Для лучшего восприятия следует научить малыша составу. Методика заключается в трех шагах:
Теперь нужно приложить усилия к запоминанию. Ребенок должен наизусть, не считая, запомнить все возможные комбинации слагаемых, дающих одну сумму. Не нужны длинные занятия. Успех придет быстрее, когда урок на запоминание будет быстрым, как перерыв между лепкой или рисованием.
Связь между сложением и вычитанием
Если ребенок все запомнил и не пытается «посчитать», можно приступать к следующему шагу. При замене знакомых карточек новыми, малыш должен писать сразу ответы. Приступаем к самому сложному – вычитать, используя знание составляющих. Вначале необходимо повторить карточки с действиями. Потом нужно спросить у ребенка, что будет с результатом, если убрать одно из слагаемых.
Данная цепочка поможет оценить связь сложения с вычитанием методом запоминания. Ученик должен понять, что вспомнить знакомое сочетание легче, чем считать в уме. В дальнейшем принцип поможет легче освоить решение линейных уравнений.
Когда можно решать примеры в пределах 20
При полном усвоении навыков счета до 10 рекомендуют приступить к действиям на втором десятке. Здесь необходимо только понимание, без подсказки и списывания у соседа. Как научить считать и разъяснять примеры ребенку в пределах 20? Следует придерживаться пошаговой методики:
Пазлы для счета до 20
Примеры с переходом через десяток требуют развивать навыки устного счета. Знание состава числа при равной сумме облегчают запоминание алгоритма расчета по действиям на сложение и вычитание в пределах 100.
Как научить решать примеры в уме?
Для облегчения устного счета эффективны упражнения для ежедневной тренировки. К шести годам детвора может самостоятельно сосчитать количество конфет, кубиков или мячиков. Им не нужно использовать свои пальчики. Родителям необходимо вовремя подсказать, направить малыша для формирования навыков решения примеров в уме. Ребенок должен освоить:
Визуальное восприятие счета – решение в столбик поможет быстрее научиться считать устно. Педагоги начального обучения рекомендуют начинать с простого. Сосчитать количество фруктов, от ребенка нужно услышать итоговый ответ, без проговаривания последовательных цифр числового ряда.
Несколько уроков, и малыш поймет, что можно сразу называть сумму. Для усложнения спрашивают, а если добавить еще три груши, сколько всего будет фруктов. «Добавки» не должно быть перед глазами. Юному счетоводу придется представить в уме и дать правильный ответ.
Следует устно повторять примеры на состав, учитывая все возможные двузначные пары. Для облегчения задачи можно применить карточки, затем полностью отказаться от них, перейдя целиком на устный счет. Все задания легче выполнять в течение дня, чтобы освоить быстрее счет:
Важно! Каждый ребенок имеет особенности развития, одному будет легче усвоить материал, другой может схватывать на лету. Нужно грамотно направлять и помогать изучать азы математики.
Дети тренируются в устном счете
Интересные способы научить прибавлять и отнимать
Ребенок должен запомнить многие числовые комбинации. Чтобы помочь лучше понять этот материал, рекомендуется предложить ему следующие задачи:
Поможет усвоить устный счет игра в интервал между значениями. Мама говорит, что загадала определенное число в промежутке от 5 до 18. Ребенок должен угадать, если он ошибается, взрослый определяет место в ряду, регулируя поиски словами «больше», «меньше», «добавь один», «отними два».
Ребенку будет сложно понять на уроках математику в первом классе, если он не усвоил технику счета. Терпение, игровые методы, непринужденность и регулярность упражнений это необходимые условия для успешного обучения. Даже одна десятая материала, усвоенного ребенком самостоятельно, поможет освоить школьную программу.