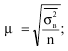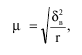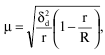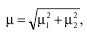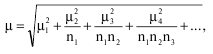Что нельзя отнести к формам представления выборки
Математическая статистика
Описательная статистика
Способы представления выборки
Результаты наблюдений x1,…,xn генеральной совокупности X, записанные в порядке их регистрации, обычно труднообозримы и неудобны для дальнейшего анализа. Одной из задач описательной статистики является получение такого представления выборки, которое позволит выявить характерные особенности совокупности исходных данных.
Одним из самых простых преобразований статистических данных является их упорядочивание по величине. Вариационным рядом выборки x1,…,xn называется способ её записи, при котором элементы упорядочиваются по возрастанию, т.е. вариационный ряд выборки – это последовательность чисел
Можно показать, что функции распределения экстремальных порядковых статистик имеют вид:
При большом числе вариантов (например, при наблюдении случайной величины непрерывного типа с высокой точностью измерений) выборка может быть представлена в виде группированного статистического ряда. Для этого отрезок [x(1); x(n)], содержащий все элементы выборки, разбивается на k непересекающихся интервалов J1 = [α0 = x(1); α1), J2 = [α1; α2),…, Jk = [αk-1; αk = x(n)], как правило, одинаковой ширины h. Правые границы всех интервалов, за исключением последнего, задаются открытыми, чтобы исключить попадание граничных точек в соседний интервал.
Число интервалов k выбирают, как правило, в зависимости от объёма выборки. Для ориентировочной оценки числа k можно воспользоваться формулой Стерджесса (Herbert Sturges, 1926):
Например, при n = 100 оценка числа интервалов по формуле Стерджесса даёт k ≈ 7, при n = 1000: k ≈ 10.
Ширина группировочных интервалов и число групп связаны формулой
Более теоретически обоснованный подход к выбору ширины группировочных интервалов дают формула Скотта (David Scott, 1979):
и формула Фридмана (David Freedman, 1981):
где s – среднеквадратичное отклонение выборки, Δ – интерквартильный размах выборки. Число группировочных интервалов k определяется из (3).
В случае если распределение генеральной совокупности существенно отличается от нормального, число интервалов может быть увеличено. С уменьшением числа интервалов k происходит потеря статистической информации, содержащейся в исходной выборке.
Наряду с частотами ni, i = 1,…,k, попадания выборочных значений в группировочные интервалы рассматриваются также:
– относительные накопленные частоты mi / n.
Полученные результаты сводятся в таблицу, называемую таблицей частот группированной выборки (табл. 1.2).
Что нельзя отнести к формам представления выборки
1. Задачи математической статистики.
4. Статистическое распределение выборки.
5. Эмпирическая функция распределения.
6. Полигон и гистограмма.
7. Числовые характеристики вариационного ряда.
8. Статистические оценки параметров распределения.
9. Интервальные оценки параметров распределения.
1. Задачи и методы математической статистики
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным- контролируемый размер детали.
Иногда проводят сплошное исследование, т.е. обследуют каждый объект относительно нужного признака. На практике сплошное обследование применяется редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов (выборочную совокупность) и подвергают их изучению.
Основная задача математической статистики заключается в исследовании всей совокупности по выборочным данным в зависимости от поставленной цели, т.е. изучение вероятностных свойств совокупности: закона распределения, числовых характеристик и т.д. для принятия управленческих решений в условиях неопределенности.
Генеральная совокупность – это совокупность объектов, из которой производится выборка.
Выборочная совокупность (выборка) – это совокупность случайно отобранных объектов.
Если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n = 100.
При составлении выборки можно поступить двумя способами: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки делятся на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Выборка должна правильно представлять пропорции генеральной совокупности. Выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществлять случайно.
Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается; в предельном случае, когда рассматривается бесконечная генеральная совокупность, а выборка имеет конечный объем, это различие исчезает.
В американском журнале «Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов относительно исхода предстоящих выборов президента США в 1936 году. Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве источника для генеральной совокупности исследуемых американцев были взяты справочники телефонных абонентов. Из них случайным образом были выбраны 4 миллиона адресов., по которым редакция журнала разослала открытки с просьбой высказать свое отношение к кандидатам на пост президента. Обработав результаты опроса, журнал опубликовал социологический прогноз о том, что на предстоящих выборах с большим перевесом победит Ландон. И … ошибся: победу одержал Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная часть населения, которые поддерживали взгляды Ландона.
На практике применяются различные способы отбора, которые можно разделить на 2 вида:
1. Отбор не требует расчленения генеральной совокупности на части (а) простой случайный бесповторный; б) простой случайный повторный).
2. Отбор, при котором генеральная совокупность разбивается на части. (а) типичный отбор; б) механический отбор; в) серийный отбор).
Простым случайным называют такой отбор, при котором объекты извлекаются по одному из всей генеральной совокупности (случайно).
Типичным называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типичной» части. Например, если деталь изготавливают на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных «типичных» частях генеральной совокупности.
Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой отбор может не обеспечивать репрезентативность выборки (если отбирают каждый 20-ый обтачиваемый валик, причем сразу же после отбора производится замена резца, то отобранными окажутся все валики, обточенные затупленными резцами).
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергают сплошному обследованию. Например, если изделия изготавливаются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.
На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы.
4. Статистическое распределение выборки
Если количество вариант велико или выборка производится из непрерывной генеральной совокупности, то вариационный ряд составляется не по отдельным точечным значениям, а по интервалам значений генеральной совокупности. Такой вариационный ряд называется интервальным. Длины интервалов при этом должны быть равны.
Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (суммы частот, попавших в этот интервал значений)
Точечный вариационный ряд частот может быть представлен таблицей:
4. Способы отбора и виды выборки
4. Способы отбора и виды выборки
В теории выборочного метода разработаны различные способы отбора и виды выборки, обеспечивающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. Этот способ отбора построен по схеме «возвращенного шара». При таком способе отбора вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется независимо от числа отбираемых единиц. При бесповторном отборе каждая единица, отобранная в случайном порядке, после ее обследования в генеральную совокупность не возвращается. Этот способ отбора построен по схеме «невозвращенного шара». Вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора.
В зависимости от методики формирования выборочной совокупности различают следующие основные виды выборки: собственно случайную, механическую, типическую (стратифицированную, районированную), серийную (гнездовую), комбинированную, многоступенчатую, многофазную, взаимопроникающую.
Собственно случайная выборка формируется в строгом соответствии с научными принципами и правилами случайного отбора. Для получения собственно-случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц. Случайный порядок – это порядок, равносильный жеребьевке. На практике такой порядок лучшим образом обеспечивается при использовании специальных таблиц случайных чисел. Если, например, из совокупности, содержащей 1587 единиц, следует отобрать 40 единиц, то из таблицы отбирают 40 четырехзначных чисел, которые меньше 1587.
При бесповторном способе отбора расчета стандартной ошибки осуществляется с помощью формулы:
– доля единиц генеральной совокупности, не попавших в выборку.
Так как эта доля всегда меньше единицы, то ошибка при бесповторном отборе при прочих равных условиях всегда меньше, чем при повторном. Бесповторный отбор практически организовать всегда легче, чем повторный, и он применяется чаще.
Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно, а иногда невозможно, так как при использовании таблиц случайных чисел необходимо пронумеровать все единицы генеральной совокупности. Довольно часто генеральная совокупность такая большая, что провести подобную предварительную работу чрезвычайно сложно и нецелесообразно. Поэтому на практике применяют другие виды выборок, каждая из которых не является строго случайной. Однако организуются они так, чтобы было обеспечено максимальное приближение к условиям случайного отбора.
При чисто механической выборке вся генеральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, составленного в каком-то нейтральном по отношению к изучаемому признаку порядке, например по алфавиту. Затем список единиц отбора разбивается на столько равных частей, сколько необходимо отобрать единиц. Далее по заранее установленному правилу, не связанному с вариацией исследуемого признака, из каждой части списка отбирается одна единица. Этот вид выборки не всегда может обеспечить случайный характер отбора, и полученная выборка может оказаться смещенной. Объясняется это тем, что, во-первых, упорядочение единиц генеральной совокупности может иметь элемент неслучайного характера. Во-вторых, отбор из каждой части генеральной совокупности при неправильном установлении начала отсчета может также привести к ошибке смещения. Однако практически легче организовать механическую выборку, чем собственно случайную, и при проведении выборочных обследований чаще всего пользуются этим видом выборки. Типическая (районированная, стратифицированная) выборка преследует две цели:
1) обеспечить представительство в выборке соответствующих типических групп генеральной совокупности по интересующим исследователя признакам;
2) увеличить точность результатов выборочного обследования.
Поскольку средняя из групповых дисперсий всегда меньше общей дисперсии, постольку при прочих равных условиях стандартная ошибка типической выборки будет меньше стандартной ошибки собственно-случайной выборки.
При определении стандартных ошибок типической выборки применяются следующие формулы:
1) при повторном способе отбора:
2) при бесповторном способе отбора:
где ? в 2 – средняя из групповых дисперсий в выборочной совокупности.
Серийная (гнездовая) выборка – это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Серийную выборку практически организовать и провести легче, чем отбор отдельных единиц. Однако при этом виде выборки, во-первых, не обеспечивается представительство каждой из серий, и, во-вторых, не устраняется влияние межсерийной вариации изучаемого признака на результаты обследования. В том случае, когда эта вариация значительна, она приведет к увеличению случайной ошибки репрезентативности. При выборе вида выборки исследователю необходимо учитывать это обстоятельство.
Стандартная ошибка серийной выборки определяется по формулам:
1) при повторном способе отбора:
где ? в 2 – межсерийная дисперсия выборочной совокупности;
г – число отобранных серий;
2) при бесповторном способе отбора:
где R – число серий в генеральной совокупности.
В практике те или иные способы и виды выборок применяются в зависимости от цели и задач выборочных обследований, а также возможностей их организации и проведения. Чаще всего применяется комбинирование способов отбора и видов выборки. Такие выборки получили название комбинированных. Комбинирование возможно в разных сочетаниях: механической и серийной выборки, типической и механической, серийной и собственно-случайной и т. д. К комбинированной выборке прибегают с целью обеспечить наибольшую репрезентативность с наименьшими трудовыми и денежными затратами на организацию и проведение обследования.
При комбинированной выборке величина стандартной ошибки выборки состоит из ошибок на каждой ее ступени и может быть определена как корень квадратный из суммы квадратов ошибок соответствующих выборок. Так, если при комбинированной выборке в сочетании использовались механическая и типическая выборки, то стандартную ошибку можно определить по формуле:
где ? 1 и ? 2– стандартные ошибки соответственно механической и типической выборок.
Особенность многоступенчатой выборки состоит в том, что выборочная совокупность формируется постепенно, по ступеням отбора. На первой ступени с помощью заранее определенного способа и вида отбора отбираются единицы первой ступени. На второй ступени из каждой единицы первой ступени, попавшей в выборку, отбираются единицы второй ступени и т. д. Число ступеней может быть и больше двух. На последней ступени формируется выборочная совокупность, единицы которой подлежат обследованию. Так, например, для выборочного обследования бюджетов домашних хозяйств на первой ступени отбираются территориальные субъекты страны, на второй – районы в отобранных регионах, на третьей в каждом муниципальном образовании отбираются предприятия или организации и, наконец, на четвертой ступени в отобранных предприятиях отбираются семьи.
Таким образом, выборочная совокупность формируется на последней ступени. Многоступенчатая выборка более гибкая, чем другие виды, хотя в общем она дает менее точные результаты, чем выборка того же объема, но сформированная в одну ступень. Однако при этом она имеет одно важное преимущество, которое заключается в том, что основу выборки при многоступенчатом отборе нужно строить на каждой из ступеней только для тех единиц, которые попали в выборку, а это очень важно, так как нередко готовой основы выборки нет.
Стандартную ошибку выборки при многоступенчатом отборе при группах разных объемов определяют по формуле:
n 1, n 2, n 3,… – численность выборок на соответствующих ступенях отбора.
В том случае, если группы неодинаковы по объему, теоретически этой формулой пользоваться нельзя. Но если общая доля отбора на всех ступенях постоянна, то практически расчет по этой формуле не приведет к искажению величины ошибки.
Сущность многофазной выборки состоит в том, что на основе первоначально сформированной выборочной совокупности образуют подвыборку, из этой подвыборки – следующую подвы-борку и т. д. Первоначальная выборочная совокупность представляет собой первую фазу, подвыборка из нее – вторую и т. д. Многофазную выборку целесообразно применять в нескольких случаях:
1) если для изучения различных признаков требуется неодинаковый объем выборки;
2) если колеблемость изучаемых признаков неодинакова и требуемая точность различна;
3) если в отношении всех единиц первоначальной выборочной совокупности (первая фаза) необходимо собрать одни – менее подробные сведения, а в отношении единиц каждой последующей фазы другие – более подробные. Одним из несомненных достоинств многофазной выборки является то обстоятельство, что сведениями, полученными на первой фазе, можно пользоваться как дополнительной информацией на последующих фазах, информацией второй фазы – как дополнительной информацией на следующих фазах и т. д. Такое использование сведений повышает точность результатов выборочного обследования.
При организации многофазной выборки можно применять сочетание различных способов и видов отбора (типическую выборку с механической и т. д.). Многофазный отбор можно сочетать с многоступенчатым. На каждой ступени выборка может быть многофазной.
Стандартная ошибка при многофазной выборке рассчитывается на каждой фазе в отдельности в соответствии с формулами того способа отбора и вида выборки, при помощи которых формировалась ее выборочная совокупность.
Взаимопроникающие выборки – это две или более независимые выборки из одной и той же генеральной совокупности, образованные одним и тем же способом и видом. К взаимопроникающим выборкам целесообразно прибегать, если необходимо за короткий срок получить предварительные итоги выборочных обследований. Взаимопроникающие выборки эффективны для оценки результатов обследования. Если в независимых выборках результаты одинаковы, то это свидетельствует о надежности данных выборочного обследования. Взаимопроникающие выборки иногда можно применять для проверки работы различных исследователей, поручив каждому из них провести обследование разных выборок.
Стандартная ошибка при взаимопроникающих выборках определяется так же, как при типической пропорциональной выборке. Взаимопроникающие выборки по сравнению с другими видами требуют больших трудовых затрат и денежных расходов, поэтому исследователь должен учитывать это обстоятельство при проектировании выборочного обследования.
Предельные ошибки при различных способах отбора и видах выборки определяются по формуле:
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
3.4. Способы и виды инвестирования за рубежом для российского инвестора
3.4. Способы и виды инвестирования за рубежом для российского инвестора Человеческая природа является дико эмоциональной, а значит, люди склонны к беспорядочному накоплению критической массы, что приводит к бумам и разорениям. Бартон Биггс Вначале поговорим о способах
3.4. Способы и виды инвестирования за рубежом для российского инвестора
3.4. Способы и виды инвестирования за рубежом для российского инвестора Человеческая природа является дико эмоциональной, а значит, люди склонны к беспорядочному накоплению критической массы, что приводит к бумам и разорениям. Бартон Биггс Вначале поговорим о способах
Формирование выборки
Формирование выборки Процедура выборки является неотъемлемым этапом проекта внутреннего аудита. Она подробно описана в различных источниках, посвященных теме аудита. Однако во многом такие описания носят академичный характер. Предлагаю заострить внимание на тех
7. Виды и способы статистического наблюдения
7. Виды и способы статистического наблюдения Статистическое наблюдение представляет собой процесс, который с точки зрения его организации может иметь разнообразные способы, формы и виды проведения. Задачей общей теории статистики явля–ется определение сущности
30. Способы отбора и виды выборки. Собственно случайная выборка
30. Способы отбора и виды выборки. Собственно случайная выборка В теории выборочного метода разработаны раз–личные способы отбора и виды выборки, обеспечи–вающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной со–вокупности.
31. Механическая и типическая выборки
31. Механическая и типическая выборки При чисто механической выборке вся ге–неральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, со–ставленного в каком-то нейтральном по отношению к изучаемому признаку порядке. Затем список
2. Виды и способы статистического наблюдения
2. Виды и способы статистического наблюдения Статистическое наблюдение представляет собой процесс, который с точки зрения его организации может иметь разнообразные способы, формы и виды проведения. Задачей общей теории статистики является определение сущности
8. Виды и способы статистического наблюдения
8. Виды и способы статистического наблюдения Рассмотрим следующие виды статистического наблюдения:1) если обследованию подвергается абсолютно все единицы изучаемой совокупности явлений и процессов, то это сплошное статистическое наблюдение;2) если обследованию
35. Виды и схемы отбора
35. Виды и схемы отбора Размер ошибки выборки и методы ее определения зависят от вида и схемы отбора.Различают четыре вида отбора совокупности единиц наблюдения.1. Случайный отбор – наиболее распространенный способ отбора в случайной выборке, его еще называют методом
36. Ошибки выборки
36. Ошибки выборки Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом. Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор,
Важность размера выборки
Важность размера выборки Как я уже говорил, люди склонны уделять слишком много внимания редким случаям возникновения какого-то феномена, несмотря на то что со статистической точки зрения из нескольких случаев невозможно извлечь много информации. Это – основная причина
Репрезентативные выборки
Репрезентативные выборки Репрезентативность наших тестов для целей предсказания будущего определяется двумя факторами:– Количество рынков: тесты, проводимые на различных рынках, будут, скорее всего, включать рынки с разной степенью волатильности типов
Размер выборки
Размер выборки Концепция размера выборки проста: для того чтобы делать статистически достоверные заключения, нужно иметь достаточно большую выборку. Чем меньше выборка, тем грубее выводы, которые можно сделать; чем выборка больше, тем выводы качественнее. Нет никакого
2. Формы, виды и способы статистического наблюдения
2. Формы, виды и способы статистического наблюдения К основным организационным формам статистического наблюдения относят: отчетность и специально организованное наблюдение.Важнейшей формой статистического наблюдения является отчетность.Отчетность – это форма
2. Виды и схемы отбора
2. Виды и схемы отбора Размер ошибки выборки и методы ее определения зависят от вида и схемы отбора.Различают четыре вида отбора совокупности единиц наблюдения:1) случайный;2) механический;3) типический;4) серийный (гнездовой).Случайный отбор – наиболее распространенный
3. Ошибки выборки
3. Ошибки выборки Каждая единица при выборочном наблюдении должна иметь равную с другими возможность быть отобранной – это является основой собственнослучайной выборки.Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством