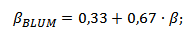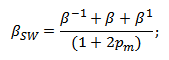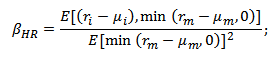Что не влияет на коэффициент бета

Коэффициенты альфа и бета. Выбираем акции в портфель «по науке»

Основы современной портфельной теории заложил в 1964 г. Г. Марковиц, а ее дальнейшему развитию поспособствовал его ученик У. Шарп. Основная идея была в том, чтобы предложить количественные характеристики, отражающие доходность и риск для каждой ценной бумаги. Тогда для формирования портфеля нужно будет всего лишь выбирать бумаги так, чтобы показатель доходности был как можно выше, а показатель риска — как можно ниже. В первую очередь необходимо было каким-то образом измерить риск.

Коэффициент Бета

Доходность рынка акций обычно оценивают по рыночным индексам. Индекс формируется из корзины бумаг — ее динамика наиболее точно будет отражать притоки или оттоки денег. Для российского рынка основным индикатором выступает индекс МосБиржи, для рынка США — S&P500.

Именно волатильность доходности актива (или рынка в целом) была взята за основу для количественной характеристики риска. Чем больше доходность актива может отклоняться от ожидаемого значения, тем выше риск, связанный с инвестиции в него.

Марковиц и его последователи считали, что в среднем доходность каждой акции стремится к доходности всего рынка. Но на коротких временных промежутках она может существенно отличаться. Одни акции оказываются менее волатильными, чем рынок, другие напротив — более волатильные. Эти отклонения от динамики рынка стали мерой риска инвестиций в конкретную акцию. Шарп назвал этот показатель «бета» (β) и предложил следующую формулу для ее определения:

Если Бета равна единице, это значит, что акция колеблется вместе с рынком и ее риск эквивалентен общерыночному. Значение беты больше единицы говорит о повышенном риске, меньше единицы — о пониженном.

Например, если бета коэффициент акции равен 2, это значит, что при росте рынка на 1% цена акции вырастет на 2%. И наоборот, если рынок снизится на 1%, то цена акции снизится на 2%.

Достаточно редко, но все-таки встречается отрицательное значение беты, которое означает, что в рассматриваемый промежуток времени между акцией и индексом наблюдалась обратная зависимость: когда индекс рос, акция снижалась, и наоборот.

На рынке США можно встретить термин high-beta stock. Этим термином обозначают высоковолатильные акции, стоимость которых колеблется существенно сильнее, чем рыночный индекс. Эти бумаги пользуются популярностью среди опытных внутридневных трейдеров, которые охотятся за широкими направленными движениями. Для более долгосрочных инвесторов такие акции несут в себе повышенные риски, и инвесторы предпочитают относиться к ним с особой осторожностью.

Марковиц и Шарп придерживались мнения, что рынок эффективен, то есть вся общедоступная информация быстро закладывается в цену и отдельный инвестор не может получить преимущество перед другими участниками. Это значит, что нарастить доходность инвестиций можно исключительно за счет увеличения риска.

Соответственно формирование портфеля сводится к подбору такой беты, которая обеспечивала бы инвестору допустимый уровень риска, который соответствовал бы его целям. Консервативные инвесторы стремятся, чтобы бета была меньше или равна 1. Участники рынка, рассчитывающие на рост рынка, стараются увеличить бету портфеля так, чтобы получить повышенную доходность.

Бета портфеля определяется, как сумма бет входящих в него акций, умноженных на вес каждой акции.

Ожидаемая доходность портфеля в таком случае выражается формулой:

Такой подход является основой так называемого пассивного инвестирования, когда управляющий не пытается искать способы, чтобы обыграть рынок, а просто формирует портфель с оптимальной бетой и с какой-то периодичностью проводит ребалансировку, ожидая получить доходность, соответствующую риску на долгосрочной дистанции.

Коэффициент Альфа

Однако не все в то время разделяли гипотезу эффективного рынка. Это подтверждалось тем, что многим управляющим удавалось опережать рынок. Из доходности портфеля вычитали доходность рынка и полученное значение считалось эффектом мастерства управляющего.

Но в таком случае никак не учитывалось то, что повышенная доходность могла стать следствием банального принятия на себя повышенного риска. Поэтому результата управляющего нужно было как-то отделить от премии за риск портфеля.

В 1968 г. Майкл Дженсен поставил задачу измерить реальную эффективность управляющих активами с учетом рисков. Так в формуле доходности портфеля появилась еще одна переменная, которая получила название коэффициента альфа (α), и приняла следующий вид:

Соответственно, коэффициент альфа можно было рассчитать через бету и ожидаемую доходность:

Альфа позволила учесть в формуле мастерство управляющего. В случае пассивного инвестирования α считается равной нулю, так как управляющий не принимает активных действия. В случае активного управления α может принимать положительные значения в случае успеха, или отрицательные значения в случае неэффективного управления.

Сегодня коэффициент альфа, помимо анализа деятельности управляющих, получил более широкое применение. В частности, показатель рассчитывается применительно к отдельной акции. Здесь альфа обозначает доходность акции, которая считается независимой от рынка.

Положительная альфа указывает на то, что на рассматриваемом промежутке времени акция стабильно опережает рынок. Например, если α=1, значит акция стабильно опережает рынок на 1%.

Согласно портфельной теории, построение портфеля с максимальной альфой при минимальной бете является способом сформировать наиболее доходный портфель при минимальном риске.

Недостатки классической портфельной теории

Основным недостатком моделей Марковица и Шарпа является предположение об эффективности рынка, при котором доходность всегда строго коррелирует с риском. Однако на практике даже при современном уровне развития ни один рынок не может в полной мере считаться эффективным в силу неравномерности распространения информации.

Кроме того, эффективный рынок предполагает, что участники действую рационально, то есть трезво оценивают риски и ориентируются исключительно на выгоду. Однако в 2000-х это предположение было развеяно несколькими учеными, лауреатами нобелевской премии, занимавшимися поведенческой экономикой. Подробнее о поведенческой экономике можно прочесть в материале: Уроки Талера: нобелевский лауреат о правилах инвестирования

Другим математическим изъяном в формуле расчета коэффициента β является предположение о нормальном распределении доходности портфеля, которое также является идеализированным и на практике в чистом виде встречается довольно редко. Кроме того, нет однозначного мнения, какая выборка исторических данных для расчета коэффициента будет достаточной, чтобы ожидать аналогичной динамики портфеля в будущем.

Тем не менее работы Шарпа и Марковица широко применяются в построении диверсифицированных портфелей и дают возможность снизить волатильность стоимости портфеля. Подробнее о построении портфеля по методу Марковица читайте в материалах: Составление инвестиционного портфеля по Марковицу для чайников и Составление инвестиционного портфеля по Марковицу — 2. Российский рынок

БКС Брокер

Последние новости

Рекомендованные новости

Главное за неделю. Скок-отскок

Итоги торгов. Еще одна неделя в минусе

Рынок нефти 2022. Сколько будет стоить баррель в новом году

Как зарабатывать на облигациях в период изменения ставок

Главное за неделю. Скок-отскок

Банк России повысил ключевую ставку до 8,5%

Акции, которые обеспечат будущее вашим детям

В погоне за трендами. Роскосмос тянется к IPO?

Адрес для вопросов и предложений по сайту: bcs-express@bcs.ru

* Материалы, представленные в данном разделе, не являются индивидуальными инвестиционными рекомендациями. Финансовые инструменты либо операции, упомянутые в данном разделе, могут не подходить Вам, не соответствовать Вашему инвестиционному профилю, финансовому положению, опыту инвестиций, знаниям, инвестиционным целям, отношению к риску и доходности. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «Компания БКС» не несет ответственности за возможные убытки инвестора в случае совершения операций, либо инвестирования в финансовые инструменты, упомянутые в данном разделе.

Информация не может рассматриваться как публичная оферта, предложение или приглашение приобрести, или продать какие-либо ценные бумаги, иные финансовые инструменты, совершить с ними сделки. Информация не может рассматриваться в качестве гарантий или обещаний в будущем доходности вложений, уровня риска, размера издержек, безубыточности инвестиций. Результат инвестирования в прошлом не определяет дохода в будущем. Не является рекламой ценных бумаг. Перед принятием инвестиционного решения Инвестору необходимо самостоятельно оценить экономические риски и выгоды, налоговые, юридические, бухгалтерские последствия заключения сделки, свою готовность и возможность принять такие риски. Клиент также несет расходы на оплату брокерских и депозитарных услуг, подачи поручений по телефону, иные расходы, подлежащие оплате клиентом. Полный список тарифов ООО «Компания БКС» приведен в приложении № 11 к Регламенту оказания услуг на рынке ценных бумаг ООО «Компания БКС». Перед совершением сделок вам также необходимо ознакомиться с: уведомлением о рисках, связанных с осуществлением операций на рынке ценных бумаг; информацией о рисках клиента, связанных с совершением сделок с неполным покрытием, возникновением непокрытых позиций, временно непокрытых позиций; заявлением, раскрывающим риски, связанные с проведением операций на рынке фьючерсных контрактов, форвардных контрактов и опционов; декларацией о рисках, связанных с приобретением иностранных ценных бумаг.

Приведенная информация и мнения составлены на основе публичных источников, которые признаны надежными, однако за достоверность предоставленной информации ООО «Компания БКС» ответственности не несёт. Приведенная информация и мнения формируются различными экспертами, в том числе независимыми, и мнение по одной и той же ситуации может кардинально различаться даже среди экспертов БКС. Принимая во внимание вышесказанное, не следует полагаться исключительно на представленные материалы в ущерб проведению независимого анализа. ООО «Компания БКС» и её аффилированные лица и сотрудники не несут ответственности за использование данной информации, за прямой или косвенный ущерб, наступивший вследствие использования данной информации, а также за ее достоверность.

Источник

Коэффициент бета. Формула. Расчет в Excel для ОАО «Газпром». Современные модификации

Разберем такой инвестиционный показатель как – коэффициент бета, рассчитаем его на реальном пример с помощью Excel и рассмотрим различные современные модификации.

Инфографика: Коэффициент бета

Оценка стоимости бизнеса	Финансовый анализ по МСФО	Финансовый анализ по РСБУ
Расчет NPV, IRR в Excel	Оценка акций и облигаций

Коэффициент бета. Определение

Коэффициент бета (англ. Beta, β, beta coefficient) – определяет меру риска акции (актива) по отношению к рынку и показывает чувствительность изменения доходности акции по отношению к изменению доходности рынка. Коэффициент бета может быть рассчитан не только для отдельной акции, но также и для инвестиционного портфеля. Коэффициент используется как мера систематического риска, и применяется в модели У.Шарпа – оценки капитальных активов CAPM (Capital Assets Price Model). В первые, коэффициент бета рассмотрел Г. Марковиц для оценки систематического риска акций, который получил называние индекс недиверсифицируемого риска. Коэффициент бета позволяет сравнивать между собой акции различных компаний по степени их риска.

Формула расчета коэффициента бета

где:

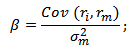
β – коэффициент бета, мера систематического риска (рыночного риска);

r_i – доходность i-й акации (инвестиционного портфеля);

r_m – рыночная доходность;

σ 2 _m – дисперсия рыночной доходности.

★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности

★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Анализ уровня риска по значению коэффициента бета (β)

Коэффициент бета показывает рыночный риск акции и отражает чувствительность изменения акции по отношению к изменению доходности рынка. В таблице ниже показана оценка уровня риска по коэффициенту бета. Коэффициент бета может иметь как положительный, так и отрицательный знак, который показывает положительную или отрицательную корреляцию между акцией и рынком. Положительный знак отражает, что доходность акций и рынка изменяются в одном направлении, отрицательный ­– разнонаправленное движение.

Значение показателя

Уровень риска акции

Направление изменения доходности акции

Данные для построения коэффициента бета информационными компаниями

Информационные компании

Можно заметить, что Bloomberg проводит краткосрочную оценку показателя, тогда как Barra и Value Line используют месячные данные доходностей акций и рынка за последние пять лет. Долгосрочная оценка может сильно быть искажена вследствие влияния на акции компании различных кризисов и негативных факторов.

Коэффициент бета в модели оценки капитальных активов – CAPM

Формула расчета доходности акций по модели капитальных активов CAPM (Capital Assets Price Model, модель У.Шарпа) имеет следующий вид:

где:

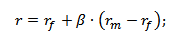
r – будущая ожидаемая доходность акций компании;

r_f – доходность по безрисковому активу;

r_m – доходность рынка;

β – коэффициент бета (мера рыночного риска), отражает чувствительность изменения стоимости акций компании в зависимости от изменения доходности рынка (индекса);

Модель CAPM была создана У.Шарпом (1964) и Дж. Линтером (1965) и позволяет спрогнозировать будущее значение доходности акции (актива) на основании линейной регрессии. Модель отражает линейную взаимосвязь планируемой доходности с уровнем рыночного риска, выраженного коэффициентом бета.

Доходность по безрисковому активу, на практике, берется как доходность по государственным ценным бумагам ГКО, ОФЗ. Доходность по ним в России составляет около 12%. Доходность можно посмотреть на сайте ЦБ в разделе «Ставки рынка ГКО-ОФЗ».

Для расчета рыночной доходности используют доходность индекса или фьючерса на индекс (индекс ММВБ, РТС ­– для России, S&P500 – США).

Пример расчета коэффициента бета в Excel

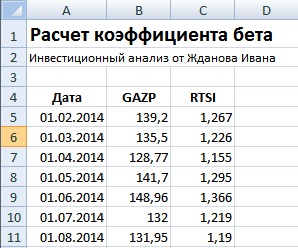
Рассчитаем коэффициент бета в Excel для отечественной компании ОАО «Газпром». Данная компания имеет обыкновенные акции, котировки которых можно посмотреть на сайте finam.ru в разделе «Экспорт данных». Для расчета были взяты месячные котировки акции ОАО «Газпром» (GAZP) и индекса РТС (RTSI) за период с 31.01.2014 по 31.01.2015 г.

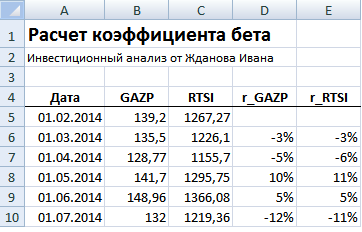
Далее необходимо рассчитать доходности по акции и индексу, для этого воспользуемся формулами:

Для расчета коэффициента бета необходимо рассчитать коэффициент линейной регрессии между доходностью акций ОАО «Газпром» и индекса РТС. Рассмотрим два варианта расчета коэффициента бета средствами Excel.

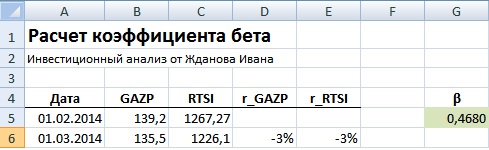
Вариант №1. Расчет через формулу Excel

Расчет через формулы Excel выглядит следующим образом:

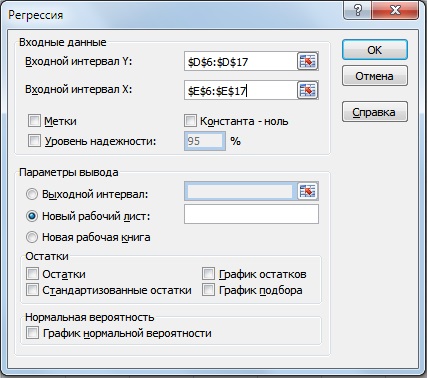
Вариант №2. Расчет через надстройку «Анализ данных»

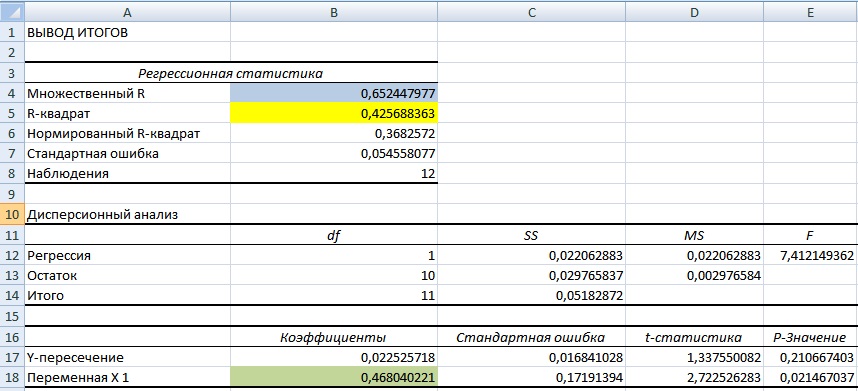
Второй вариант расчета коэффициента бета использует надстройку Excel «Анализ данных». Для этого необходимо перейти в главном меню программы в раздел «Данные», выбрать опцию «Анализ данных» (если данная надстройка включена) и в инструментах анализа выделить «Регрессия». В поле «Входной интервал Y» выбрать доходности акции ОАО «Газпром», а в поле «Выходные интервал X» выбрать доходности индекса РТС.

Далее мы получим отчет по регрессии на отдельном листе. В ячейке В18 показано значение коэффициента линейной регрессии, который равен коэффициенту бета = 0,46. Также проанализируем другие параметры модели, так показатель R-квадрат (коэффициент детерминированности) показывает силу взаимосвязи между доходностью акции ОАО «Газпром» и индекса РТС. Коэффициент детерминированности равен 0,4, что является довольно мало для точного прогнозирования будущей доходности по модели CAPM. Множественный R – коэффициент корреляции (0,6), который показывает наличие зависимости между акцией и рынком.

Значение 0,46 коэффициента бета для акции свидетельствует о умеренном риске и в тоже время сонаправленность изменения доходностей.

★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Недостатки использования коэффициента бета в модели CAPM

Рассмотрим ряд недостатков присущих данному коэффициенту:

Модификация коэффициента бета

Так как коэффициент, предложенный У. Шарпов не имел должной устойчивости и не мог использоваться для прогнозирования будущей доходности в модели CAPM, различными учеными были предложены модификации и корректировки данного показателя (англ. adjusted beta, modified beta).Рассмотрим скорректированные коэффициенты бета:

Модификация коэффициента бета от М.Блюма (1971)

Маршал Блюм показал, что со временем коэффициенты бета компаний стремятся к 1. Формула расчета скорректированного показателя следующая:

Использование данных весовых значений позволяет более точно спрогнозировать будущий систематический риск. Так данную модификацию используют многие информационные агентства, такие как: Bloomberg, Value Line и Merrill Lynch.

Модификация коэффициента бета от Бава-Линдсберга (1977)

В своей корректировке Линдсберг предложил рассчитывать односторонний коэффициент бета. Главный постулат заключался в том, что изменение доходности выше определенного уровня большинство инвесторов не рассматривают как риск, а риском считается только то, что ниже уровня. За минимальный уровень риска в данной модели был доходность безрискового актива.

где:

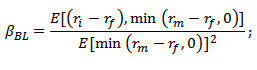
r_i – доходность акции; r_m – доходность рынка; r_f – доходность безрискового актива.

Модификация коэффициента бета от Шоулза-Виллимса

β_-1, β, β₁ – коэффициенты беты для предыдущего (-1) текущего и следующего (1) периода;

ρ_m – коэффициент автокорреляции рыночной доходности.

Модификация коэффициента бета от Харлоу-Рао (1989)

Формула отражает одностороннюю бету, с предположением, что инвесторы рассматривают риск только как отклонение от среднерыночной доходности вниз. В отличие от модели Бава-Линдсберга за минимальный уровень риска брался уровень среднерыночной доходности.

где: μ_i – средняя доходность акции; μ_m – средняя доходность рынка;

Помимо коэффициента бета на практике используют другие показатели риска-доходности инвестиционного портфеля, ПИФа, более подробно узнать про современные показатели оценки инвестиций вы можете в моей статье: «Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel«. О практике оценке риска инвестиции читайте в статье: «Методы оценки риска VaR (Value at Risk). Рыночный риск. Пример расчета в Excel «.

Коэффициент бета для акций США

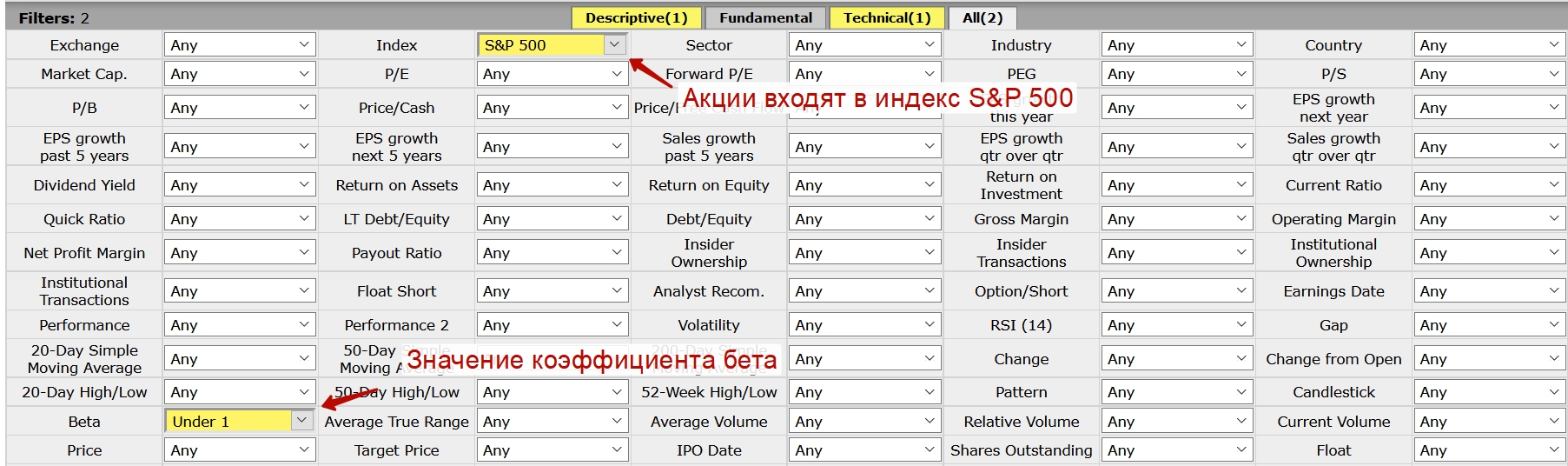
Существуют сервисы позволяющие оценить коэффициент бета для множества компаний и выделить наиболее интересные. Будем применять сервис Finviz. Чтобы найти акции менее чувствительные чем колебания фондового рынка необходимо установить коэффициент бета меньше 1.

Фильтрация акций США по бета меньше «1» позволяет найти акции для консервативного инвестора, изменчивость которых ниже изменения индекса S&P 500

Где посмотреть коэффициент бета для российских акций

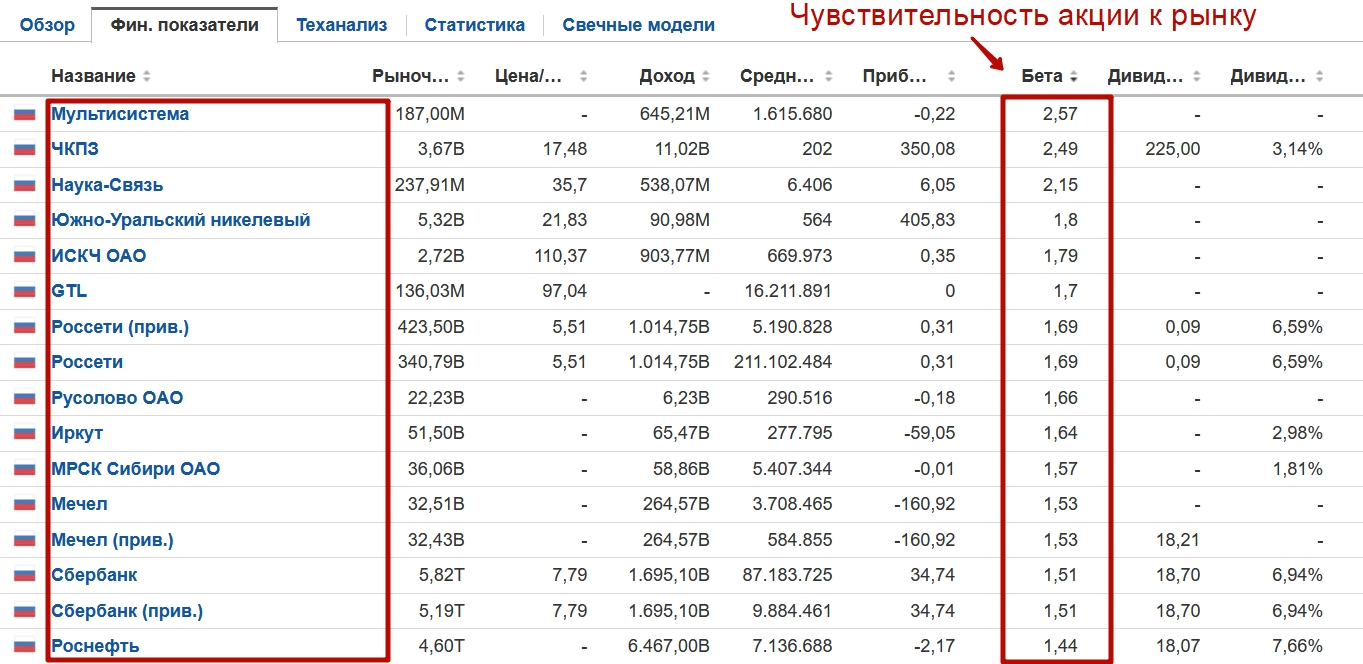
Если цель узнать коэффициент бета для российских акций, то для этого можно воспользоваться сервисом investing.com. Помимо отечественных компаний коэффициент бета можно определить для иностранных. Как мы видим для акции Мультисистемы коэффициент равен 2,57 – это значит, что она в 2,5 раза более изменчивая по отношению к рыночному изменению (индексу ММВБ).

Проанализировать акции на бета можно по ссылке.

Сортировка отечественных акций по коэффициента бета. Чем выше значение тем более изменчива акция по отношению к индексу ММВБ

Высокие значения коэффициента бета при растущем рынке будут обеспечивать дополнительную прибыль, при коррекциях такие акции как правило имеют больше убытков.

Резюме

Коэффициент бета является одним из классических мер рыночного риска для оценки доходности акций, инвестиционных портфелей и ПИФов. Несмотря на сложность использования данного инструмента для оценки отечественных низколиквидных акций и неустойчивость его изменения во времени, коэффициент бета является ключевым показателем оценки инвестиционных рисков. Рассмотренные модификации коэффициента позволяют скорректировать и дать более оценку систематическому риску. С вами был Иван Жданов, спасибо за внимание.

Автор: к.э.н. Жданов Иван Юрьевич

Источник