Что называют значением числового выражения 7 класс
Значение числового, буквенного выражения и выражения с переменными
В процессе разбора тем о числовых, буквенных выражениях и выражениях с переменными следует обратить внимание на понятие значение выражения. Ниже дадим определение этому термину, рассмотрим примеры.
Что такое значение числового выражения
Мы знакомимся с числовыми выражениями с самого начала школьного обучения. Да и почти сразу начинает использоваться понятие «значение числового выражения». Так обозначают выражения, составляющие которого – числа, соединяемые знаками арифметических действий: плюс, минус, умножить, разделить.
Значение числового выражения – это конечное число, получаемое в результате выполнения заданных действий в исходном числовом выражении.
Зачастую в словосочетании «значение числового выражения» слово «числовое» не употребляют, поскольку в любом случае понятно, значение какого выражения рассматривается.
В основном интерес вызывает не само числовое выражение, а его значение. Практически всегда существует задача по нахождению значения заданного выражения, которая так и обозначается: «найти значение выражения». В соответствующей статье можно детально изучить сам процесс нахождения значения числовых выражения разного рода с примерами.
Значение буквенного выражения и выражения с переменными
Кроме числовых, интерес представляют и буквенные выражения – те выражения, составляющими которого являются, в том числе, одна или несколько букв. Буквы в буквенном выражении обозначают разные числа, и при замене букв на числа получается числовое выражение.
Значения букв – числа, которые заменяют эти буквы в буквенном выражении. Тогда значение буквенного выражения при заданных значениях букв – это значение полученного числового выражения.
Таким образом, речь идет не о значении буквенного выражения, как такового, а о его значении, когда заданы (определены) конкретные значения букв.
В программе алгебры буквы в буквенном выражении могут принимать разнообразные значения, тогда буквы называют переменными, а буквенные выражения – выражениями с переменными. Логично следует введение понятия значения выражений при выбранных значениях переменных.
Значение выражения с переменными при выбранных значениях переменных – это значение числового выражения, полученное при подстановке конкретных выбранных значений переменных в заданное выражение.
Возможен вариант, когда выбранные переменные –различны, а значение исходного выражения при этих переменных одинаково.
Значения переменных возможно задать из областей допустимых значений, которые им соответствуют, поскольку в ином случае, подставив значения, не принадлежащие области допустимых значений, можно получить числовое выражение, не имеющее смысла.
Алгебра. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Числовое выражение – это выражение, состоящее из чисел, знаков математических действий и скобок.
Значение числового выражения – результат выполненных арифметических действий в числовом выражении.
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
«Числа не управляют миром, но показывают, как управляется мир» – однажды сказал немецкий писатель Иоганн Гёте. Сегодня пойдёт речь именно о числах и арифметических операциях с ними.
Мы уже неоднократно решали задачи, в которых над заданными числовыми значениями приходится выполнять арифметические действия, такие как сложение, вычитание, умножение и деление. Иногда в том или ином задании все перечисленные действия встречаются одновременно, поэтому чтобы верно вычислить значение того или иного выражения или решить задачу, нужно сначала задать правильный порядок действий.
Порядок арифметических действий.
Арифметические действия выполняются слева направо:
1) действие в скобках;
2) операции умножения или деления;
3) сложения или вычитания.
Таким образом, мы подошли к определению понятия числового выражения.
Числовое выражение – это выражение, состоящее из чисел, знаков математических действий и скобок.
Например, числовые выражения могут выглядеть так:
Если в данных выражениях выполнить все действия, т.е. получить ответ в виде действительного числа, то говорят, что получено значение числового выражения. Например, в этих числовых выражениях значения соответственно равны 8,5 и 195.
Но всегда ли можно получить значение числового выражения?
Рассмотрим следующее выражение:
В данном случае выражение не имеет смысла, т.к. на некотором этапе вычисления требуется делить на ноль, но на ноль делить нельзя. Таким образом, числовое выражение имеет смысл при условии что делитель (если таковой есть) не равен нулю.
Стоит отметить, что числовое выражение может состоять только из числа.
Например, 45 и 1/2 – тоже числовые выражения.
Как уже отмечалось ранее, числовые выражения иногда используют и для решения задач.
Решим такую задачу:
Автомобиль двигался по трассе 20 км со скоростью 100 км/ч, а затем ещё 30 км со скоростью 90 км/ч. Какова средняя скорость автомобиля на всём участке?
Для решения задачи нужно вспомнить, что средняя скорость – это отношение всего пути, пройденного телом ко времени прохождения всего пути.
Исходя из этого, составим числовые выражения, необходимые для решения задачи.
Сначала найдём путь, который преодолел автомобиль.
20 +30 = 50 (км) – весь путь автомобиля.
Далее найдём все потраченное автомобилем время на прохождение трассы.
+ = (ч) – время движения автомобиля по всей трассе.
Остаётся определить среднюю скорость автомобиля при движении по трассе:
50: = 93,75 (км/ч) – средняя скорость движения автомобиля по трассе.
Это и есть искомый ответ к данной задаче.
Эту же задачу можно решить, используя следующую таблицу.
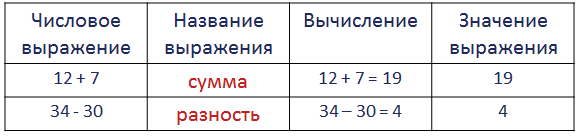
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
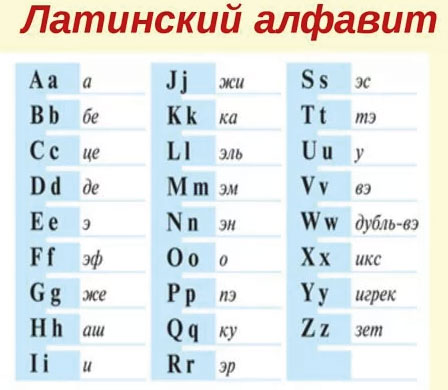
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Алгебра. 7 класс
Конспект урока
Числовое значение целого выражения. Тождественное равенство целых выражений
Перечень рассматриваемых вопросов:
Равенство между буквенными выражениями, называют тождество, если оно превращается в верное числовое равенство, при подстановке в него вместо букв любых чисел.
Для доказательств тождеств используются свойства одночленов, многочленов и правила действия над ними.
Нулевые многочлены, равные 0, тождественны.
Ненулевые многочлены, равные 0, не тождественны.
Для любого целого выражения при любых числовых значениях входящих в него букв, соответствующее числовое выражение имеет смысл.
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Перед нами несколько выражений, можно ли из них составить числовое выражение?
Можно, если вместо букв подставим числа.
(16а – 15х)(3 + 4а) + (х + у)
Сегодня мы узнаем, как это сделать.
Как было сказано ранее, если в целое выражение подставить вместо букв числа, то получим числовое выражение.
Подставим его в выражение (17 + с) и получим:
Пусть а = 1; х = 3; у = –1.
Подставим его в выражение: (16а – 15х)(3 + 4а) + (х + у) и получим:
Результаты вычислений числовых выражений называют числовым значением целого выражения.
Стоит отметить, что для любого целого выражения, при любых числовых значениях входящих в него букв, соответствующее числовое выражение имеет смысл, т. к. не содержит деления на ноль, исходя из определения целого выражения.
Рассмотрим теперь равенство одночленов.
Оно превращается в верное числовое равенство, если в нём заменить буквы числами, т. к. в левой и в правой части будет стоять произведение чисел, но с переставленными множителями, а произведение чисел не зависит от порядка множителей.
3 · 4 · 5 · 5 · 4 · 5 · 5 = 3 · 4 · 4 · 5 · 5 · 5 · 5.
Когда говорят, что в равенстве буквы заменяют числами, то имеют ввиду, что одна и та же буква, где бы она не находилась в равенстве, заменяется одним и тем же числом.
Рассмотрим равенство многочленов.
Равенство между буквенными выражениями называют тождество, если оно превращается в верное числовое равенство при подстановке в него вместо букв любых чисел.
( а + 3) · (а + 3) = (а + 3) 2
Тождество, так как при a = 2 равенство сохраняется:
(2 + 3) · (2 + 3) = (2 + 3) 2
В математике тождества очень часто приходится доказывать. Поэтому, для доказательства тождества используются ранее изученные нами свойства одночленов, многочленов и правила действия над ними.
Стоит отметить, что нулевые многочлены, равны нулю тождественно, т. е при любых числовых значениях букв, числовое значение целого выражения будет равно нулю.
Ненулевые многочлены, равные 0, не тождественны.
Ненулевые многочлены могут обращаться в ноль при определённых числовых значениях букв, а при других значениях букв, многочлен не обратиться в ноль.
а + с, обратится в ноль, только при а = –с,
k – х, обратится в ноль, только при k = х.
х 2 + у 2 + 1, не обратится в ноль ни при каких числовых значениях х и у.
А теперь рассмотрим, как доказывать тождество.
Рассмотрим задание. Докажите тождество:
(7а + с)(16а – 5с) = 112а 2 – 19ас – 5с 2
(7а + с)(16а – 5с) = 7а·16а + 7а·(-5)с + 16ас + с(-5)с = 112а 2 – 35ас + 16ас – 5с 2 = 112а 2 – 19ас – 5с 2
Для доказательства, преобразуем левую часть равенства, применив правило умножения многочленов, затем приведём подобные члены.
В результате преобразования левая и правая часть равенства оказались равны, что и требовалось доказать.
А теперь рассмотрим, как можно доказывать неравенства. Рассмотрим следующее задание.
Докажите, что для любых чисел а и с верно следующее неравенство:
Для любого числа а число а 4 ≥ 0.
Для любого числа с число с 4 ≥ 0.
Итак, сегодня мы получили представление о том, что такое тождество и как найти числовое значение целого выражения.
Для углублённого изучения материала.
Докажем следующее тождество.
у(2х + у)(2х – у) + 5у 2 = 4х 2 у – у 2 (у – 5)
Для доказательства тождества будем преобразовывать как правую, так и левую часть равенства.
Для этого раскроем скобки, используя правила умножения многочлена на многочлен и одночлена на многочлен, затем приведем к стандартному виду полученные выражения.
у(2х + у)(2х – у) + 5у 2 = у(2х2х + 2х(-у) + 2ху – уу) + 5у 2 = у(4х 2 – у 2 ) + 5 у 2 = 4х 2 у – у 3 + 5у 2
4х 2 у – у 2 (у – 5) = 4х 2 у – у 2 у + 5 у 2 = 4х 2 у – у 3 + 5у 2
В результате преобразования левая и правая часть равенства оказались равны, что и требовалось доказать.
Разбор заданий тренировочного модуля.
1. Вычислите числовое значение выражения при а = х = 1
(3ааааа + 2х) (3а 5 – 2х) + 4х 2
Для решения задания, нужно упростить выражение, используя правило умножения многочлена на многочлен, затем привести полученный многочлен в стандартный вид и привести подобные члены.
(3ааааа + 2х) (3а 5 – 2х) + 9х 2 = (3а 5 + 2х) (3а 5 – 2х) +9х 2 = 3а 5 · 3а 5 + (–2х) · 3а 5 + 2х · 3а 5 – 2х · 2х + 9х 2 = 9а 10 – 6а 5 х + 6а 5 х – 4х 2 + 4х 2 = 9а 10 = 9 · 1 = 9.
2. Найдите периметр закрашенного прямоугольника при а = 40 см, c = 0,8 м, k = 50 см.
Для выполнения задания, нужно вспомнить, что такое периметр – это сумма всех сторон многоугольника. Периметр прямоугольника, это сумма его четырёх сторон а + а + (с + k) + (с + k). Но стоит обратить внимание на сторону с, она выражена в метрах и требует перевода в см, т. е. с = 0,8 м = 8 (см).
Периметр прямоугольника равен:
40 см + 40 см + 80 см + 80 см + 50 см + 50 см = 340 (см).