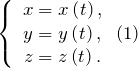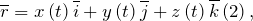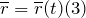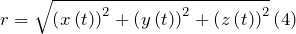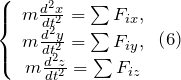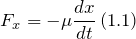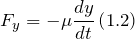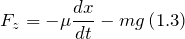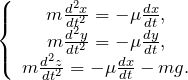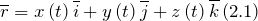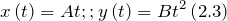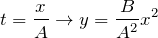Что называют законом движения
Закон движения
Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.
В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида
Закон движения может быть найден, в зависимости от задачи, либо из дифференциальных законов механики (см. Законы Ньютона), либо из интегральных (см. Закон сохранения энергии, Закон сохранения импульса), либо из так называемых вариационных принципов.
Смотреть что такое «Закон движения» в других словарях:
закон движения — judėjimo dėsnis statusas T sritis fizika atitikmenys: angl. law of motion vok. Bewegungsgesetz, n rus. закон движения, m pranc. loi de mouvement, f … Fizikos terminų žodynas
закон движения механики Ньютона — Niutono mechanikos dėsnis statusas T sritis fizika atitikmenys: angl. law of Newtonian mechanics vok. Newtonsches Bewegungsgesetz, n rus. закон движения механики Ньютона, m pranc. loi du mouvement de Newton, f … Fizikos terminų žodynas
закон движения центра масс — masių centro judėjimo dėsnis statusas T sritis fizika atitikmenys: angl. center of mass law vok. Satz vom Massenmittelpunkt, m; Schwerpunktsatz, m rus. закон движения центра масс, m pranc. loi de mouvement du centre de masse, f … Fizikos terminų žodynas
ЗАКОН — необходимое, существенное, устойчивое, повторяющееся отношение между явлениями. 3. выражает связь между предметами, составными элементами данного предмета, между свойствами вещей, а также между свойствами внутри вещи. Существуют 3.… … Философская энциклопедия
Закон о возвращении — (ивр. Хок hа Швут חוק השבות ), закон, провозглашающий право каждого еврея репатриироваться в Государство Израиль. Принят Кнессетом 5 июля 1950 года. Этот закон юридически выражает идеологическую доктрину сионизма, лежащую в основе возникновения… … Википедия
Закон Бернулли — является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости: Здесь плотность жидкости, скорость потока, высота, на которой находится рассматриваемый… … Википедия
Закон Видемана — Франца — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм … Википедия
Закон толерантности Шелфорда — Закон максима Шелфорда закон, согласно которому существование вида определяется лимитирующими факторами, находящимися не только в минимуме, но и в максимуме. Закон толерантности расширяет закон минимума Либиха. Формулировка «Лимитирующим… … Википедия
закон — ЗАКОН (nomos греч.) понятие и термин, исторически возникшие применительно к регуляции общественных отношений и в дальнейшем перенесенные на понимание природы. Генезис понятия 3. в древнегреческой философии был связан с такими… … Энциклопедия эпистемологии и философии науки
Законы движения материальной точки
Кинематические законы движения
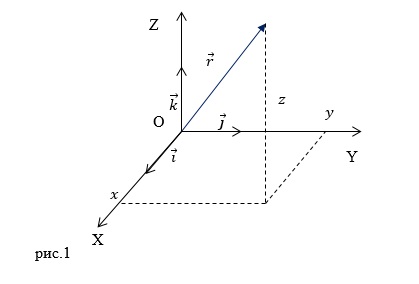
Механическим движением называют изменение положения тела относительно тел, составляющих систему отсчета. Для того чтобы описать движение тела следует выбрать систему отсчета в которую ходят: тело отсчёта, система координат, которая связана с телом отсчета и часы (отсчет времени). Движение можно описать при помощи трех способов: координатного (скалярного), векторного, траекторного (натурального).
В декартовой системе координат (рис.1) положение материальной точки (M) определяют три координаты (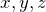
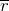
Если точка перемещается, то в любой следующий момент времени координаты изменяются:
Уравнения (1) называют скалярными кинематическими уравнениями движения материальной точки (параметрическими уравнениями). Данные уравнения определяют перемещение точки координатным способом.
Радиус- вектор можно определить как:
где 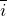
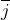
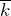
является векторным кинематическим уравнением движения материальной точки. Выражения 1-3 называют кинематическими законами движения материальной точки. Данные законы полностью описывают движение точки.
Модуль (длина) радиус- вектора 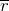
Динамические законы движения материальной точки
Динамика рассматривает движение материальной точки в зависимости от сил, которые к ней приложены. Основные законы классической динамики сформулированы Ньютоном.
Первый закон Ньютона:
Материальная точка не изменяет своего состояния покоя или движется равномерно и прямолинейно, если внешние силы на нее не действуют или действие их взаимно скомпенсированы.
Второй закон Ньютона:
В инерциальных системах отсчета результирующая сил (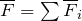
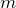
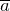
Дифференциальные уравнения движения материальной точки записываю как:
где 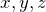
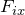
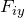
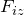
С помощью дифференциальных уравнений перемещения материальной точки при известной массе находят силы, которые действуют на точку.
Примеры решения задач
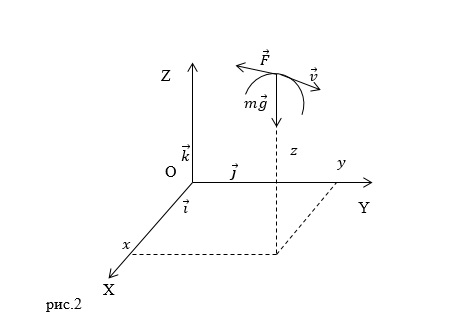
| Задание | На материальную точку действуют сила тяжести (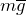 ) и сила сопротивления, пропорциональная скорости ( ) и сила сопротивления, пропорциональная скорости (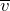 ) движения точки ( ) движения точки (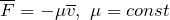 ) (рис.2). Составьте динамические уравнения движения материальной точки. ) (рис.2). Составьте динамические уравнения движения материальной точки. |
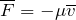 являются выражения:
являются выражения:Применяя второй закон Ньютона выражения (1.1) — (1.3) преобразуем к виду:
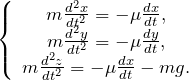
В условии задачи радиус 0 вектор задан как:
Следовательно, сравнивая выражения (2.1) и (2.2) имеем:
Выразим из первого уравнения (2.3) время и подставим его во второе уравнение, получим:
Уравнение траектории — это парабола (рис.3).
Закон движения тела: определение, формулы
Каждый обращал внимание на все многообразие видов движения, с которыми он сталкивается в своей жизни. Однако любое механическое движение тела сводится к одному из двух типов: линейное или вращательное. Рассмотрим в статье основные законы движения тел.
О каких типах движения пойдет речь?
Как было отмечено во введении, все виды движения тела, которые рассматриваются в классической физике, связаны либо с прямолинейной траекторией, либо с круговой. Любые другие траектории можно получить благодаря комбинации этих двух. Далее в статье будут рассмотрены следующие законы движения тела:
Равномерное движение, или состояние покоя

Впоследствии Исаак Ньютон сформулировал свой первый закон движения тела, согласно которому скорость последнего является постоянной величиной всегда, когда нет внешних сил, изменяющих характеристики движения.
Равномерное прямолинейное перемещение тела в пространстве описывается следующей формулой:
Перемещение по прямой с ускорением
Согласно второму закону Ньютона, наличие внешней силы, действующей на тело, неминуемо приводит к появлению ускорения у последнего. Из определения ускорения (быстрота изменения скорости) следует выражение:

a = v / t или v = a * t
Если действующая на тело внешняя сила будет оставаться постоянной (не будет изменять модуля и направления), то ускорение также не изменится. Такой тип движения называется равноускоренным, где ускорение выступает коэффициентом пропорциональности между скоростью и временем (скорость растет линейно).
Для этого движения пройденный путь рассчитывается с помощью интегрирования скорости по времени. Закон движения тела для пути при равноускоренном перемещении приобретает форму:
Самым распространенным примером этого движения является падение любого предмета с высоты, при котором сила тяжести сообщает ему ускорение g = 9,81 м/с2.
Прямолинейное ускоренное (замедленное) движение с наличием начальной скорости
По сути, речь идет о комбинации двух видов перемещения, рассмотренных в предыдущих пунктах. Представим простую ситуацию: автомобиль ехал с некоторой скоростью v0, затем водитель нажал на тормоза, и транспортное средство через некоторое время остановилось. Как описать движение в этом случае? Для функции скорости от времени справедливо выражение:
Как и в предыдущем пункте, если взять интеграл по времени от v(t), то получаем формулу для пути:
Отметим, что по этой формуле вычисляется только путь торможения. Чтобы узнать расстояние, пройденное автомобилем за все время его движения, следует найти сумму двух путей: для равномерного и для равнозамедленного движения.
В примере описанном выше, если бы водитель нажал не на педаль тормоза, а на педаль газа, тогда в представленных формулах поменялся бы знак «-» на «+».
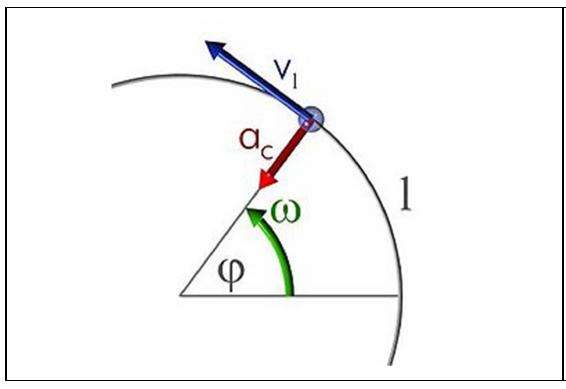
Движение по окружности
Любое движение по окружности не может происходить без ускорения, поскольку даже при сохранении модуля скорости изменяется ее направление. Ускорение, которое связано с этим изменением, называется центростремительным (именно оно искривляет траекторию тела, превращая ее в окружность). Модуль этого ускорения вычисляют так:
В этом выражении скорость может зависеть от времени, как это происходит в случае равноускоренного движения по окружности. В последнем случае ac будет быстро расти (квадратичная зависимость).
Вращение вокруг оси с постоянной скоростью
Этот вид движения идентичен предыдущему, только описывать его принято не с использованием линейных физических величин, а с применением угловых характеристик. Закон вращательного движения тела, когда угловая скорость не изменяется, в скалярной форме записывается так:
Величина ω показывает, на сколько радиан повернется тело за секунду. Величины L и I имеют такой же смысл, как импульс и масса для прямолинейного движения. Соответственно, угол θ, на который повернется тело за время t, вычисляется так:
Вращение вокруг оси с ускорением
Если к системе, которая способна вращаться, прикладывать внешнюю силу, то она начнет увеличивать свою угловую скорость. Такая ситуация описывается следующим законом движения тела вокруг оси вращения:
Для равноускоренного движения по окружности получаем, что ω зависит от времени следующим образом:
В этом случае угол поворота за время t можно определить, проинтегрировав ω по времени, то есть:
Если же тело уже вращалось с некоторой скоростью ω0, а затем начал действовать внешний момент силы F*d, то по аналогии с линейным случаем можно записать такие выражения:
θ = ω0 * t + α * t2 / 2
Таким образом, появление внешнего момента сил является причиной наличия ускорения в системе с осью вращения.
Для полноты информации отметим, что изменить скорость вращения ω можно не только с помощью внешнего момента сил, но и благодаря изменению внутренних характеристик системы, в частности ее момента инерции. Эту ситуацию видел каждый человек, который наблюдал за вращением фигуристов на льду. Группируясь, спортсмены увеличивают ω за счет уменьшения I, согласно простому закону движения тела:
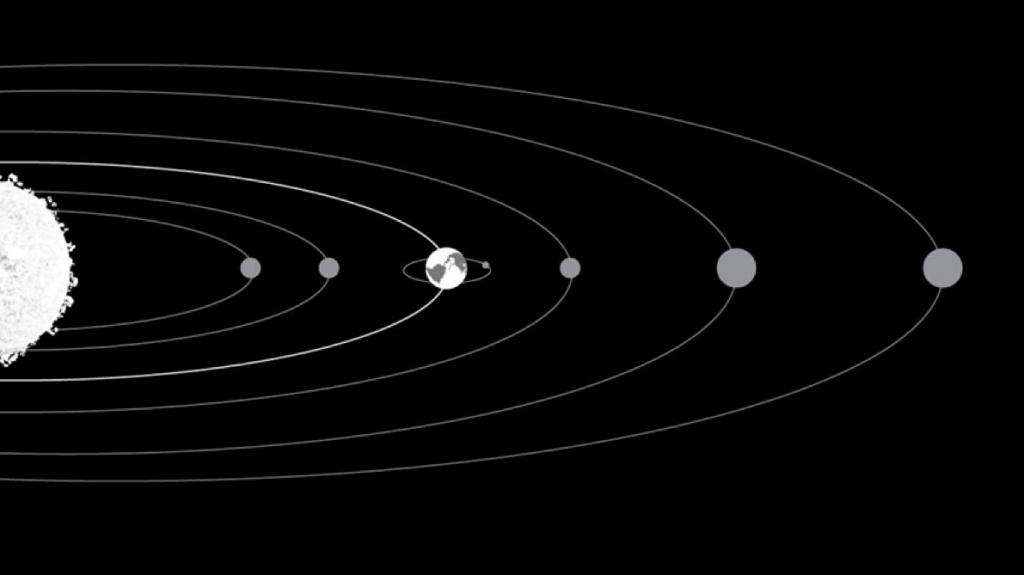
Движение по эллиптической траектории на примере планет Солнечной системы
Как известно, наша Земля и другие планеты Солнечной системы вращаются вокруг своей звезды не по окружности, а по эллиптической траектории. Впервые математические законы для описания этого вращения сформулировал знаменитый немецкий ученый Иоганн Кеплер в начале XVII века. Используя результаты наблюдений своего учителя Тихо Браге за движением планет, Кеплер пришел к формулировке своих трех законов. Они формулируются следующим образом:
Впоследствии Исаак Ньютон, используя эти законы движения тел (планет), сформулировал свой знаменитый закон всемирной гравитации, или тяготения. Применяя его, можно показать, что константа C в 3-м законе Кеплера равна:
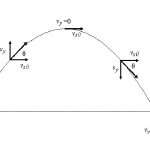
Отметим, что движение по эллиптической орбите в случае действия центральной силы (тяготения) приводит к тому, что линейная скорость v постоянно меняется. Она максимальна, когда планета находится ближе всего к звезде, и минимальна вдали от нее.
Механическое движение и его характеристики
теория по физике 🧲 кинематика
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
По типу линии, вдоль которой движется тело, выделяют два вида движения:
По скорости выделяют два вида движения:
По ускорению выделяют три вида движения:
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
Способы описания механического движения
Описать механическое движение можно двумя способами:
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
Перемещение
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).
Математическое определение модуля скорости:

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид :
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить