Что называют высотой трапеции

Высота трапеции

Что такое трапеция

Трапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.

Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.

Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как найти высоту трапеции

Через стороны

Если нам известны стороны фигуры, мы можем найти ее высоту по формуле:

Где h — высота, a — большее основание, b — меньшее основание, c и d — боковые стороны.

Через среднюю линию и площадь

Если в условии есть данные о величине средней линии и площади, можем использовать формулу:

Где m — средняя линия трапеции.

Через боковую сторону и угол

Когда нам известна величина одной из боковых сторон и угол между этой стороной и большим основанием, используем формулу:

Где \alpha — это угол между стороной c и большим основанием a.

Через диагонали, угол между ними и основания

Если нам известны длины обоих диагоналей трапеции, а также угол между ними, можем найти высоту следующим образом:

Где \(d_1\) и \(d_2\) — диагонали трапеции, а \(\gamma\) — угол между ними.

Через диагонали, угол и среднюю линию

В том случае, если нам известны сразу длины диагоналей, угол между ними и величина средней линии, мы можем узнать высоту трапеции по формуле:

Через радиус вписанной окружности

Если в трапецию можно вписать окружность, то ее высота будет равна диаметру этой окружности, то есть d=h. Другими словами, высота фигуры будет равна удвоенному радиусу вписанной в нее окружности:

Где r — радиус выписанной окружности.

Примеры вычисления

Дана трапеция, в которой известны основания a и b. Они равны 4,5 см и 2,5 см. Также известны ее боковые стороны d и c, равные 2 см и \(2\sqrt2\) см соответственно. Найти высоту.

Чтобы решить эту задачу, используем формулу \(h=\sqrt^2+d^2+c^2><2\cdot(a-b)>>)^2.\)

Подставляем известные значения:

Чтобы найти высоту, нужно знать величину средней линии m. Определим ее следующим образом:

Теперь используем формулу \(h=\frac Sm\) и подставим известные значения:

Мы знаем, что сторона c трапеции равна \(\sqrt2\) см, а угол \(\alpha\) между известной стороной и основанием равен 45 градусов. Найти значение высоты.

Используем формулу \(h=c\cdot\sin\left(\alpha\right)\) и подставим значения:

Для решения задачи использует формулу \(h=\frac\cdot\sin\left(\gamma\right).\)

Источник

Трапеция. Определение, виды, свойства

Определения

Определение 1. Трапецией называется четырехугольник, у которого две стороны параллельны а две другие − нет.

На Рис.1 четырехугольники ABCD и EFGH являются трапециями.

Параллельные стороны трапеции называются основаниями трапеции, а непараллельные стороны − боковыми сторонами (Рис.2).

В трапеции ABCD (Рис.1) углы A и B называют углами при основании AB, а углы C и D называют углами при основании CD.

Определение 2. Высотой трапеции называется перпендикуляр, отпущенный из любой точки прямой, проходящей через один из оснований трапеции, на прямую, проходящую через другое основание.

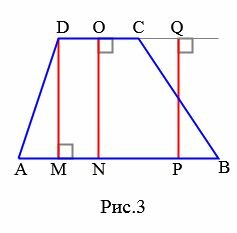На Рис.3 отрезки DM, ON, QP являются вершинами трапеции ABCD. Поскольку величина каждой из этих отрезков является расстоянием между параллельными прямыми, проходящими через основания трапеции, то они равны друг другу.

Определение 3. Средней линией трапеции называется отрезок, соединяющий средние точки боковых сторон.

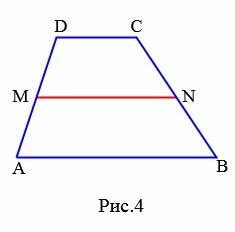На рисунке Рис.4 \( \small MN \) является средней линией трапеции \( \small ABCD, \) причем \( \small AM=MD,\;\; BN=NC. \)

Виды трапеций

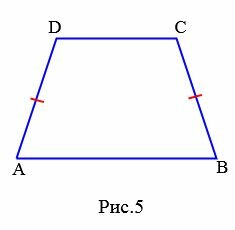
Если боковые стороны трапеции равны, то трапеция называется равнобокой или равнобедренной (Рис.5).

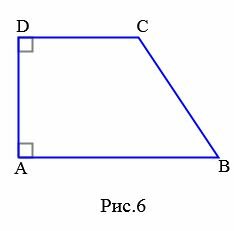
Трапеция называется прямоугольной, если одна из боковых сторон перпендикуляна основаниям трапеции (Рис.6).

Трапеция называется разносторонней, если длина всех сторон разные (т.е. если трапеция не прямоульная и не равнобедренная)(Рис.7).

Свойства трапеции

Свойство 1. Средняя линия трапеции параллельна основаниям и равна половине их суммы.

Доказательство. Пусть MN средняя линия трапеции ABCD (Рис.8). Докажем, что \( \small MN || AB, \) \( \small MN=\frac12 (AB+CD). \)

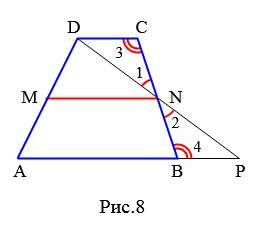Проведем прямую DN и обозначим точку ее пересечения с прямой AB точкой P. Так как MN является средней линией трапеции ABCD, то

Углы 3 и 4 являются накрест лежащими, при рассмотрении параллельных прямых BP и CD пересеченные секущей CB, тогда (теорема 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей).

Исходя из равенств (1),(2) и (3) получим, что треугольники CND и NPC равны, по второму признаку равенства треугольников. Тогда BP = DC, DN = NP. Из равенств AM = MD и DN = NP следует, что MN является средней линией треугольника ADP. Тогда \( \small MN \ || \ AP \) ( или \( \small MN \ || \ AB \)) и \( \small MN =\frac 12 AP \). Но \( \small AP=AB +BP=AB+CD \). Тогда \( \small MN =\frac 12 (AB+CD).\)

Свойство 2. Сумма углов трапеции, прилежащих к одной боковой стороне равна 180°.

Доказательство. Рассмотрим трапецию ABCD (Рис.9).

Углы A и D являутся односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Тогда \( \small \angle A+ \angle D=180°.\)

Свойство 3. Отрезок, слединяющий середины диагоналей трапеции лежит на средней линии трапеции и равен половине разности оснований.

Доказательство. Рассмотрим трапецию ABCD (Рис.10).

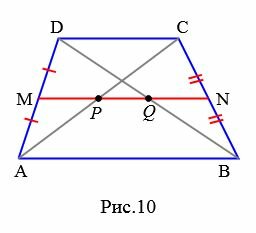Поскольку точки P и Q являются средними точками диагоналей AC и BD, соответственно, то:

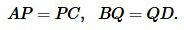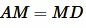
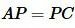
MP − является средней линией треугольника ADC, так как , . Тогда

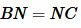
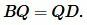
QN − является средней линией треугольника BCD, так как , Тогда

Из и следует, что P находится на прямой, проходящей через среднюю линию MN, поскольку из точки M можно провести только одну прямую, параллельно CD (Аксиома 1 статьи Аксиома параллельных прямых).

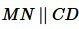
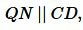
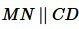
Аналогично, из и следует, что Q находится на прямой, проходящей через среднюю линию MN, поскольку из точки N можно провести только одну прямую, параллельно CD.

Далее, учитывая (4) и (5), получим:

Далее, учитывая свойство 1, получим:

Свойства равнобокой (равнобедренной) трапеции

Свойсво 1′. В равнобокой трапеции углы при каждом основании равны.

Доказательство. Рассмотрим равнобедренную (равнобокую) трапецию ABCD, где AD = BC (Рис.11).

Проведем высоты DM и CN. Поскольку DM = CN и AD = BC, то прямоугольники ADM и NCB равны гипотенузе и катету (см. статью Прямоугольный треугольник. Свойства, признаки равенства). Тогда \( \small \angle A=\angle B. \) Докажем, далее, что \( \small \angle ADC=\angle DCB. \) \( \small \angle A +\angle ADC=180° \) поскольку углы A и ADC являются односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle B +\angle DCB=180°. \) Учитывая, что \( \small \angle A=\angle B \), получим \( \small \angle ADC=\angle DCB. \)

Свойсво 2′. В равнобокой трапеции диагонали равны.

Доказательство. Рассмотрим треугольники ADC и DCB (Рис.12). Имеем CD общая сторона для обеих треугольников, AD = CB, \( \small \angle ADC=\angle DCB. \) Тогда треугольники равны по двум сторонам и углу между ними. Следовательно диагонали AC и DB трапеции ABCD равны.

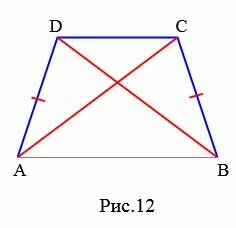Свойсво 3′. В равнобокой трапеции высота, приведенная из вершины тупого угла на основание, делит основание трапеции на отрезки, больший из которых равен половине суммы оснований, а меньший равен половине разности оснований.

Доказательство. Рассмотрим четырехугольник DMNC (Рис.11). Имеем:

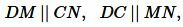Тогда четырехугольник DMNC является прямоугольником. Следовательно DC = MN. Поскольку треугольники ADM и NCB равны (см. доказательство следствия 1), то AM = NB. Следовательно:

Источник

Трапеция, ее свойства, формулы площади, высоты, сторон

Трапеция, ее свойства, формулы площади, высоты, сторон.

Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.

Трапеция (понятие, определение):

Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.

Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.

Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Виды трапеций:

Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.

Рис. 2. Равнобедренная трапеция

Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.

Прямоугольная трапеция – это трапеция, имеющая прямые углы при боковой стороне.

Рис. 3. Прямоугольная трапеция

Элементы трапеции: основания, боковые стороны, средняя линия и высота:

Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.

AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.

AD – большее основание трапеции, BC – меньшее основание трапеции.

Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.

Рис. 5. Трапеция и срединная линия

Расстояние между основаниями трапеции называется высотой трапеции.

Высота трапеции (h) определяется формулой:

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.

Свойства трапеции:

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Рис. 7. Трапеция и срединная линия

2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.

4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

Рис. 10. Трапеция

6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.

В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).

8. Диагонали трапеции делят ее на 4 треугольника.

Два из них, прилежащие к основаниям, подобны.

Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.

Треугольники ABO и CDO имеют одинаковую площадь.

9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.

BC : AD = OC : AO = OB : DO

10. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.

11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.

AK = KB, AM = MC, BN = ND, CL = LD,

KL – средняя линия, UV – отрезок, который соединяет основания трапеции

12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:

где b – большее основание трапеции, a – меньшее основание трапеции, S₁ и S₂ – площади образованных трапеций, в результате разделения средней линией.

Свойства равнобедренной трапеции:

1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.

2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.

3. Углы при любом основании равнобедренной трапеции равны.

4. Сумма противоположных углов равнобедренной трапеции равна 180°.

5. Длины диагоналей равнобедренной трапеции равны.

6. Вокруг равнобедренной трапеции можно описать окружность.

7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.

Формулы трапеции:

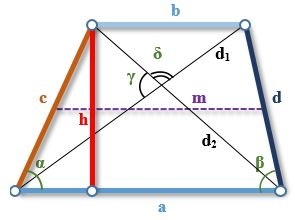
Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d₁ и d₂ – диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.

Формулы для определения сторон трапеции:

Через среднюю линию и одно из оснований трапеции:

Через высоту и углы при нижнем основании трапеции:

a = b + h · (ctg α + ctg β)

b = a – h · (ctg α + ctg β)

Через боковые стороны и углы при нижнем основании:

a = b + c· cos α + d· cos β

b = a – c· cos α – d· cos β

Через высоту и углы при нижнем основании трапеции:

Формулы для определения средней линии трапеции:

Через длины оснований трапеции:

Через площадь и высоту трапеции:

Формулы для определения высоты трапеции:

Через сторону и прилегающий угол при нижнем основании трапеции:

h = c· sin α = d· sin β

Через диагонали трапеции и углы между ними:

Через диагонали трапеции, углы между ними и среднюю линию трапеции:

Через площадь и длины оснований трапеции:

Через площадь и длину средней линии трапеции:

Формула для определения периметра трапеции:

Формулы для определения площади трапеции:

Через основания и высоту трапеции:

Через среднюю линию и высоту трапеции:

Через диагонали трапеции и угол между ними:

Через все стороны трапеции:

С помощью формулы Герона для трапеции:

Как называется объемная трапеция?

Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.

В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Мировая экономика

Справочники

Востребованные технологии

Поиск технологий

О чём данный сайт?

Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.

Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.

Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!

Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.

О Второй индустриализации

Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.

Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.

Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.

Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.

Источник