Что называют выражением каковы основные правила записи выражений

Числовые и буквенные выражения

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Числовые выражения: что это

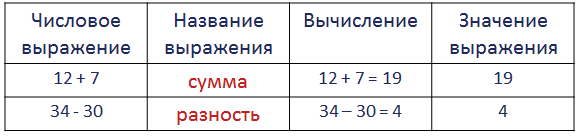
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

Это простые числовые выражения.

Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

Это сложные числовые выражения.

Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

14 больше 4
14 > 4
6 + 8 > 2 * 2

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

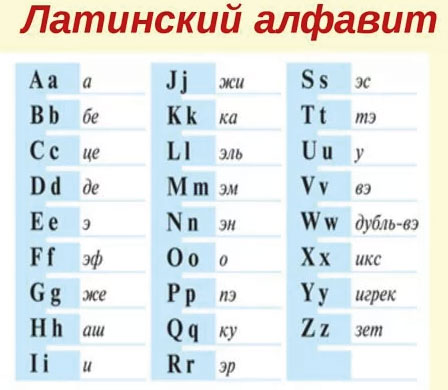
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

Пример 1. Найдите значение выражения: 5 + x.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

Выражения с переменными

Переменная — это значение буквы в буквенном выражении.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a

Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Задание раз.

Задание два.

Составьте буквенное выражение:

Сумма разности b и 345 и суммы 180 и x.

Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.

Ответ: Маша и Лена посмотрели всего 313 видео.

Источник

Числовые и буквенные выражения

Числовые выражения

В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.

Значение выражения — это результат выполненных действий.

Чтение числовых выражений

Решение числовых выражений

45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13

Сравнение значений числовых выражений

Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.

Для этого найдем значения каждого из них:

Буквенные выражения

Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.

Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.

Чаще всего используются буквы:

a, b, c, d, x, y, k, m, n

Алгоритм решения буквенного выражения

1. Прочитать буквенное выражение

2. Записать буквенное выражение

3. Подставить значение неизвестного в выражении

4. Вычислить результат

Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с

Подставим вместо неизвестного «с» число 4.

У нас получается выражение: 28 – 4

Переменные

Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.

Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства

Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:

Теперь мы можем найти значение этого выражения:

с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7

Поделись с друзьями в социальных сетях:

Источник

Что называют выражением каковы основные правила записи выражений

Во всех языках программирования под выражением подразумева­ется конструкция, составленная из констант, переменных, знаков операций, функций, скобок. Выражение определяет порядок вычис­ления некоторого значения. Если это числовое значение, то такое выражение называют арифметическим. Вот несколько примеров ариф­метических выражений, записанных по правилам языка Си:

Три первых выражения имеют традиционную форму для язы­ков программирования высокого уровня, поэтому их смысл оче­виден. Следующие четыре выражения специфичны для языка Си.

Опишем набор операций, используемых в Си, а также правила записи и вычисления выражений. Напомним, что операция, при­меняемая к одному операнду, называется унарной, а операция с двумя операндами — бинарной.

— вычитание или унарный минус;

+ сложение или унарный плюс;

++ унарная операция увеличения на единицу (инкремент);

Все операции, кроме деления по модулю, применимы к лю­бым числовым типам данных. Операция % применима только к целым числам.

Если хотя бы один из операндов имеет вещественный тип, то и ре­зультат будет вещественным. Например, операции 5./3, 5./3., 5/3. дадут вещественный результат 1.6666.

Различие проявляется при использовании префиксной и пост­фиксной форм в выражениях. Проиллюстрируем это на примерах. Первый пример:

В результате выполнения переменные получат следующие зна­чения: а = 4, b = 3, с= 6. Второй пример:

Результаты будут такими: а = 4, b = 3, с=12.

По убыванию старшинства арифметические операции распо­ложены в следующем порядке:

Одинаковые по старшинству операции выполняются в порядке слева направо. Д ля изменения порядка выполне­ния операций в выражениях могут применяться круглые скобки.

>= больше или равно, равно,

Как уже говорилось раньше, в стандарте Си нет логического типа данных. Поэтому результатом операции отношения является целое число: если отношение истинно — то 1, если ложно — то 0.

Результатом второго и третьего отношений будет 0 — ложь; результат четвертого отношения равен 1 — истина; результат пер­вого отношения зависит от значения переменной а.

! операция отрицания (НЕ),

&& конъюнкция, логическое умножение (И),

| | дизъюнкция, логическое сложение (ИЛИ).

Например, логическое выражение, соответствующее системе неравенств 0 x

Обратите внимание на то обстоятельство, что здесь не понадо­бились круглые скобки для выделения операций отношения. В Си операции отношения старше конъюнкции и дизъ­юнкции. По убыванию приоритета логические операции и опера­ции отношения расположены в следующем порядке:

Помимо рассмотренных в Си имеются поразрядные логические операции. Эти операции выполняются над каждой парой соответ­ствующих двоичных разрядов внутреннего представления операн­дов. Их еще называют битовыми логическими операциями. Знаки битовых логических операций:

& поразрядная конъюнкция (И),

| поразрядная дизъюнкция (ИЛИ),

^ поразрядное исключающее ИЛИ,

поразрядное отрицание (НЕ).

Битовые логические операции вместе с операциями поразряд­ного сдвига влево ( >) позволяют добраться до каждого бита внутреннего кода. Чаще всего такие действия прихо­дится выполнять в системных программах.

Операция присваивания. Знак операции присваивания =. Следствием отме­ченного факта является то, что присваивание, как любой другой знак операции, может несколько раз входить в выражение. На­пример:

Присваивание имеет самый низкий приоритет (ниже только у операции «запятая»). Кроме того, операция присваивания — правоассоциативная. Это значит, что несколько подряд расположен­ных присваиваний выполняются справа налево. Поэтому в приве­денном выше выражении первой выполнится операция сложе­ния, затем переменной с присвоится значение суммы, затем это значение присвоится переменной b и в конце — переменной а.

а+=2 эквивалентно а=а+2,

х-=а+ b эквивалентно х=х-(а+ b ),

р/=10 эквивалентно р=р/10,

m*=n эквивалентно m=m*n,

г%=5 эквивалентно г=г%5.

Заметим, что вместо выражения а=а+2 предпочтительнее пи­сать в программе а+=2, поскольку второе выражение будет вы­числяться быстрее.

Операция явного преобразования типа (операция «тип»). Приме­нение этой операции имеет следующий формат:

Операндом могут быть константа, переменная, выражение. В результате значение операнда преобразуется к указанному типу. Примеры использования преобразования типа:

По поводу последнего выражения заметим, что приоритет опе­рации «тип» выше деления (и других бинарных арифметических операций), поэтому сначала значение переменной х приведется к целому типу (отбросится дробная часть), а затем выполнится де­ление по модулю.

Следующий фрагмент программы иллюстрирует одну из прак­тических ситуаций, в которой потребовалось использовать преоб­разование типа:

В результате переменная с получит значение 0,5. Без преобразо­вания типа ее значение стало бы равно 0.

sizeof (тип) и sizeof (выражение)

Результатом операции является целое число, равное количе­ству байтов, которое занимает в памяти величина явно указан­ного типа или величина, полученная в результате вычисления выражения. Последняя определяется также по типу результата выражения. Хотя по форме записи это похоже на функцию, од­нако sizeof является именно операцией. Ее приоритет выше, чем у бинарных арифметических операций, логических опера­ций и отношений. Примеры использования операции:

sizeof (int) результат — 2

sizeof (1) результат — 2

sizeof (0.1) результат — 8

sizeof (1L) результат — 4

sizeof (char) результат — 1

sizeof (‘ a’) результат — 2

Операция «запятая». Эта необычная операция используется для связывания нескольких выражений в одно. Несколько выражений, разделенных запятыми, вычисляются последовательно слева на­право. В качестве результата такого совмещенного выражения при­нимается значение самого правого выражения. Например, если переменная х имеет тип int, то значение выражения (х=3, 5*х) будет равно 15, а переменная х примет значение 3.

Данная операция реализует алгоритмическую структуру ветв­ления. Алгоритм ее выполнения следующий: первым вычисляется значение выражения 1, которое обычно представляет собой некоторое условие. Если оно истинно, т.е. не равно 0, то вычисляется выражение 2 и полученный результат становится результатом опе­рации. В противном случае в качестве результата берется значение выражения 3.

Пример 1. Вычисление абсолютной величины переменной X можно организовать с помощью одной операции:

Пример 2. Выбор большего значения из двух переменных аи Ь:

Пример 3. Заменить большее значение из двух переменных аи b на единицу:

Правила языка в данном случае позволяют ставить условную операцию слева от знака присваивания.

Операции ( ) и [ ]. В языке Си круглые и квадратные скобки рассматриваются как операции, причем эти операции имеют наи­высший приоритет. Их смысл будет раскрыт позже.

Подведем итог всему разговору об операциях Си/Си++, сведя их в общую табл. 2 и расположив по рангам. Ранг операции — это порядковый помер в ряду приоритетов. Чем больше ранг, тем ниже приоритет. В таблице отражено еще одно свойство опера­ций — ассоциативность. Если одна и та же операция, повторя­ющаяся в выражении несколько раз, выполняется в порядке расположения слева направо, то она называется левоассоциа-тивной; если выполняется справа налево, то операция правоассоциативная. В таблице эти свойства отображены стрелками влево и вправо. Некоторые операции, присутствующие в таблице, пока не обсуждались.

Источник

Числовые и буквенные выражения. Формулы

Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:

Буквы и цифры в математике служат для обозначения чисел.

Цифрами обозначается конкретное, какое-то определённое число.

Буквами – любое или неизвестное число, в зависимости от задачи.

МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:

При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.

Примеры математических выражений:

ВНИМАНИЕ!

НЕ ЯВЛЯЕТСЯ математическим выражением:

Например, это НЕ математические выражения:

Случаи опускания знака умножения в выражениях

В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.

В остальных случаях знак умножения опускают, например:

Как читать математические выражения

Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:

Более сложные выражения, называют по последнему выполняемому действию:

Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:

Алгоритм чтения математических выражений

Чтобы прочитать математическое выражение, нужно:

При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.

Формулы

Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.

Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:

а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);

б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_

= v_<1>-15\).

Иначе это называется выразить одну величину через другую.

Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.

Запись такого равенства называется формулой.

ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.3 / 5. Количество оценок: 8

Источник

Порядок действий в математике

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные операции в математике

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо.

Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11- 2 + 5.

В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.

Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.

Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.

Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Подставляем полученные значения в исходное выражение:

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.

Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.

И, как всегда, рассмотрим, как это работает на примере.

В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.

Подставляем полученное значение в исходное выражение:

Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:

Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!

Источник