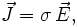Что называют удельным сопротивлением удельной электропроводностью проводника кратко ответ

Зависимость удельного сопротивления от температуры объясняется, зависимостью средней длинны свободного пробега носителя заряда от температуры. Это свойство используют в разного рода измерительных приборах и автоматических устройствах.

Удельная электропроводность вещества

Исходя из постоянства градиента температуры вдоль оси проводника, запишем, что:

Найдем интеграл от (1.2), получим:

Для вычисления сопротивления используем формулу:

Вместо k в выражение (1.7) подставим то, что получили в (1.5), имеем:

За основу решения задачи примем формулу:

Если проводник считать цилиндром длины l, то массу стержня можно найти как:

Площадь поперечного сечения проводника найдем в соответствии с формулой:

Подставим (2.3) и (2.4) в (2.1) получим:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 01 2021

Источник

Удельная проводимость

Удельная проводимость

Уде́льная проводи́мость (уде́льная электропрово́дность) — мера способности вещества проводить электрический ток. (Точнее следует говорить об электропроводности среды, т.к. не имеется в виду обязательно химически чистое вещество; эта величина различна для разных веществ или смесей, сплавов и т.п.). В линейном изотропном веществе плотность возникающего тока прямо пропорциональна электрическому полю (см. Закон Ома) Удельной проводимостью называют величину, обратную удельному сопротивлению.

В неоднородной среде σ может зависеть (и в общем случае зависит) от координат, т.е. не совпадает в различных точках проводника.

В анизотропных средах формула остаётся той же, но σ является тензором 2 ранга, и векторы плотности тока и напряжённости поля, вообще говоря, не коллинеарны.

Величина, обратная удельной проводимости, называется удельным сопротивлением.

Удельная проводимость некоторых веществ

Удельной проводимостью называют величину, обратную удельному сопротивлению. (см. удельное сопротивление).

Удельная проводимость при температуре 20 °C:

Источник данных: Кухлинг Х. Справочник по физике. Пер. с нем., М.: Мир, 1982, стр. 475 (табл. 39); значения удельной проводимости вычислены из удельного сопротивления и округлены до 3 значащих цифр.

Источник

СОДЕРЖАНИЕ

Определение

Идеальный случай

В идеальном случае поперечное сечение и физический состав исследуемого материала однородны по всему образцу, а электрическое поле и плотность тока везде параллельны и постоянны. Многие резисторы и проводники действительно имеют однородное поперечное сечение с равномерным потоком электрического тока и сделаны из одного материала, так что это хорошая модель. (См. Диаграмму рядом.) В этом случае удельное электрическое сопротивление ρ (по-гречески: rho ) можно рассчитать следующим образом:

Вышеприведенное уравнение можно транспонировать, чтобы получить закон Пуйе (названный в честь Клода Пуйе ):

Общие скалярные величины

Для менее идеальных случаев, таких как более сложная геометрия, или когда ток и электрическое поле изменяются в разных частях материала, необходимо использовать более общее выражение, в котором удельное сопротивление в конкретной точке определяется как отношение электрическое поле до плотности тока, который он создает в этой точке:

Как показано ниже, это выражение упрощается до одного числа, когда электрическое поле и плотность тока в материале постоянны.

Если электрическое поле является постоянным, электрическое поле определяется общим напряжением V на проводнике, деленным на длину ℓ проводника:

Если плотность тока постоянна, она равна полному току, деленному на площадь поперечного сечения:

Подставляя значения E и J в первое выражение, получаем:

Тензорное сопротивление

Здесь анизотропия означает, что материал имеет разные свойства в разных направлениях. Например, кристалл графита микроскопически состоит из стопки листов, и ток очень легко течет через каждый лист, но гораздо труднее от одного листа к соседнему. В таких случаях ток не течет точно в том же направлении, что и электрическое поле. Таким образом, соответствующие уравнения обобщаются до трехмерной тензорной формы:

Точно так же удельное сопротивление можно выразить в более компактной записи Эйнштейна :

В любом случае результирующее выражение для каждой компоненты электрического поля:

Аналогично определяется электропроводность:

Оба результата приводят к:

Проводимость и носители тока

Связь между плотностью тока и скоростью электрического тока

j → знак равно q п υ → а <\ displaystyle <\ vec > = qn <\ vec <\ upsilon>> _ > ,

j → знак равно ∑ j j я <\ displaystyle <\ vec > = \ sum _ j_ > .

Причины проводимости

Теория лент упрощена

Электрический ток состоит из потока электронов. В металлах существует много уровней энергии электронов вблизи уровня Ферми, поэтому существует много электронов, которые могут двигаться. Это причина высокой электронной проводимости металлов.

В металлах

В полупроводниках и изоляторах

В ионных жидкостях / электролитах

N знак равно α N 0 <\ Displaystyle N = \ альфа N_ <0>> .

Сверхпроводимость

Плазма

Дифференциация этого соотношения позволяет рассчитать электрическое поле по плотности:

Возможно получение не квазинейтральной плазмы. Электронный луч, например, имеет только отрицательные заряды. Плотность ненейтральной плазмы обычно должна быть очень низкой или очень маленькой. В противном случае отталкивающая электростатическая сила рассеивает его.

Удельное сопротивление и проводимость различных материалов

10 −13Твердая резина10 1310 −14Воздух10 9 к 10 15

От 10 −15 до 10 −9Древесина (сушка в духовке)10 14 к 10 16От 10 −16 до 10 −14Сера10 1510 −16Плавленый кварц7,5 × 10 171,3 × 10 −18ДОМАШНИЙ ПИТОМЕЦ10 2110 −21Тефлон10 23 к 10 25От 10 −25 до 10 −23

Металлические вещества отличаются от всех других материалов тем, что внешние оболочки их атомов связаны довольно непрочно и часто позволяют одному из своих электронов выходить на свободу. Таким образом, внутренняя часть металла заполнена большим количеством непривязанных электронов, которые бесцельно путешествуют, как толпа перемещенных лиц. Когда на металлическую проволоку действует электрическая сила, приложенная к ее противоположным концам, эти свободные электроны устремляются в направлении силы, образуя то, что мы называем электрическим током.

С технической точки зрения, модель свободных электронов дает базовое описание электронного потока в металлах.

Температурная зависимость

Линейное приближение

Удельное электрическое сопротивление большинства материалов изменяется с температурой. Если температура T не меняется слишком сильно, обычно используется линейное приближение :

Металлы

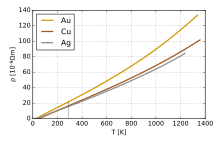
В общем, удельное электрическое сопротивление металлов увеличивается с температурой. Электрон- фононные взаимодействия могут играть ключевую роль. При высоких температурах сопротивление металла линейно увеличивается с температурой. Когда температура металла понижается, температурная зависимость удельного сопротивления подчиняется степенной функции температуры. Математически температурная зависимость удельного сопротивления металла ρ может быть аппроксимирована формулой Блоха – Грюнайзена:

Закон Видемана – Франца

Закон Видемана – Франца гласит, что коэффициент электропроводности металлов при нормальных температурах обратно пропорционален температуре:

При высоких температурах металла закон Видемана-Франца выполняется:

Полупроводники

Еще лучшее приближение температурной зависимости удельного сопротивления полупроводника дается уравнением Стейнхарта – Харта :

Внешние (легированные) полупроводники имеют гораздо более сложный температурный профиль. При повышении температуры, начиная с абсолютного нуля, их сопротивление сначала резко уменьшается, поскольку носители покидают доноры или акцепторы. После того, как большинство доноров или акцепторов потеряли своих носителей, сопротивление снова начинает немного увеличиваться из-за уменьшения подвижности носителей (как в металле). При более высоких температурах они ведут себя как собственные полупроводники, поскольку носители от доноров / акцепторов становятся незначительными по сравнению с носителями, генерируемыми термически.

В некристаллических полупроводниках проводимость может происходить за счет квантового туннелирования зарядов из одного локализованного участка в другой. Это известно как скачкообразное изменение диапазона и имеет характерную форму

где n = 2, 3, 4, в зависимости от размерности системы.

Комплексное сопротивление и проводимость

Сопротивление в зависимости от удельного сопротивления в сложной геометрии

В таких случаях формулы

должен быть заменен на

Произведение удельное сопротивление-плотность

Серебро, хотя и является наименее резистивным из известных металлов, имеет высокую плотность и по своим характеристикам аналогично меди, но намного дороже. Кальций и щелочные металлы имеют лучшие произведения удельного сопротивления, но редко используются для проводников из-за их высокой реакционной способности с водой и кислородом (и отсутствия физической прочности). Алюминий гораздо более устойчив. Токсичность исключает выбор бериллия. (Чистый бериллий также является хрупким.) Таким образом, алюминий обычно является предпочтительным металлом, когда решающим фактором является вес или стоимость проводника.

Источник

Удельное электрическое сопротивление и проводимость

СОДЕРЖАНИЕ

Определение [ править ]

Идеальный случай [ править ]

В идеальном случае поперечное сечение и физический состав исследуемого материала однородны по всему образцу, а электрическое поле и плотность тока везде параллельны и постоянны. Многие резисторы и проводники действительно имеют однородное поперечное сечение с равномерным потоком электрического тока и сделаны из одного материала, так что это хорошая модель. (См. Диаграмму рядом.) В этом случае удельное электрическое сопротивление ρ (по-гречески: rho ) можно рассчитать следующим образом:

Вышеприведенное уравнение можно транспонировать, чтобы получить закон Пуйе (названный в честь Клода Пуйе ):

Общие скалярные величины [ править ]

Для менее идеальных случаев, таких как более сложная геометрия, или когда ток и электрическое поле изменяются в разных частях материала, необходимо использовать более общее выражение, в котором удельное сопротивление в конкретной точке определяется как отношение электрическое поле до плотности тока, который он создает в этой точке:

Как показано ниже, это выражение упрощается до одного числа, когда электрическое поле и плотность тока в материале постоянны.

Если электрическое поле является постоянным, электрическое поле определяется общим напряжением V на проводнике, деленным на длину ℓ проводника:

Если плотность тока постоянна, она равна полному току, деленному на площадь поперечного сечения:

Подставляя значения E и J в первое выражение, получаем:

Тензорное сопротивление [ править ]

Здесь анизотропия означает, что материал имеет разные свойства в разных направлениях. Например, кристалл графита микроскопически состоит из стопки листов, и ток очень легко течет через каждый лист, но гораздо труднее от одного листа к соседнему. [4] В таких случаях ток не течет точно в том же направлении, что и электрическое поле. Таким образом, соответствующие уравнения обобщаются до трехмерной тензорной формы: [5] [6]

[ E x E y E z ] = [ ρ x x ρ x y ρ x z ρ y x ρ y y ρ y z ρ z x ρ z y ρ z z ] [ J x J y J z ] <\displaystyle <\beginE_\\E_\\E_\end>=<\begin\rho _&\rho _&\rho _\\\rho _&\rho _&\rho _\\\rho _&\rho _&\rho _\end><\beginJ_\\J_\\J_\end>>

Точно так же удельное сопротивление может быть дано в более компактной записи Эйнштейна :

В любом случае результирующее выражение для каждой компоненты электрического поля будет следующим:

Поскольку выбор системы координат свободен, обычное соглашение состоит в том, чтобы упростить выражение, выбрав ось x, параллельную текущему направлению, поэтому J _y = J _z = 0. Это оставляет:

Проводимость определяется аналогично: [7]

[ J x J y J z ] = [ σ x x σ x y σ x z σ y x σ y y σ y z σ z x σ z y σ z z ] [ E x E y E z ] <\displaystyle <\beginJ_\\J_\\J_\end>=<\begin\sigma _&\sigma _&\sigma _\\\sigma _&\sigma _&\sigma _\\\sigma _&\sigma _&\sigma _\end><\beginE_\\E_\\E_\end>>

Оба результата приводят к:

J x = σ x x E x + σ x y E y + σ x z E z <\displaystyle J_=\sigma _E_+\sigma _E_+\sigma _E_> J y = σ y x E x + σ y y E y + σ y z E z <\displaystyle J_=\sigma _E_+\sigma _E_+\sigma _E_> J z = σ z x E x + σ z y E y + σ z z E z <\displaystyle J_=\sigma _E_+\sigma _E_+\sigma _E_>

Электропроводность и носители тока [ править ]

Связь между плотностью тока и скоростью электрического тока [ править ]

Причины проводимости [ править ]

Упрощенная теория лент [ править ]

Электрический ток состоит из потока электронов. В металлах существует много уровней энергии электронов вблизи уровня Ферми, поэтому существует много электронов, которые могут двигаться. Это причина высокой электронной проводимости металлов.

В металлах [ править ]

В полупроводниках и изоляторах [ править ]

В ионных жидкостях / электролитах [ править ]

σ = q ( b + + b − ) α N 0 <\displaystyle \sigma =q\left(b^<+>+b^<->\right)\alpha N_<0>> ,

Сверхпроводимость [ править ]

Плазма [ править ]

Дифференциация этого соотношения позволяет рассчитать электрическое поле по плотности:

Возможно получение не квазинейтральной плазмы. Электронный луч, например, имеет только отрицательные заряды. Плотность ненейтральной плазмы обычно должна быть очень низкой или очень маленькой. В противном случае отталкивающая электростатическая сила рассеивает его.

Удельное сопротивление и проводимость различных материалов [ править ]

10 −13[45]Твердой резины10 1310 −14?[23]Воздух10 9 к 10 15

От 10 −15 до 10 −9[46] [47]Древесина (сушка в духовке)10 14 к 10 16От 10 −16 до 10 −14[43]Сера10 1510 −16?[23]Плавленый кварц7,5 × 10 171,3 × 10 −18?[23]ДОМАШНИЙ ПИТОМЕЦ10 2110 −21?Тефлон10 23 к 10 25От 10 −25 до 10 −23?

Металлические вещества отличаются от всех других материалов тем, что внешние оболочки их атомов связаны довольно непрочно и часто позволяют одному из своих электронов выходить на свободу. Таким образом, внутренняя часть металла заполнена большим количеством непривязанных электронов, которые бесцельно путешествуют, как толпа перемещенных лиц. Когда на металлическую проволоку действует электрическая сила, приложенная к ее противоположным концам, эти свободные электроны устремляются в направлении силы, образуя то, что мы называем электрическим током.

С технической точки зрения, модель свободных электронов дает базовое описание электронного потока в металлах.

Температурная зависимость [ править ]

Линейное приближение [ править ]

Удельное электрическое сопротивление большинства материалов изменяется с температурой. Если температура T не меняется слишком сильно, обычно используется линейное приближение :

ρ ( T ) = ρ 0 [ 1 + α ( T − T 0 ) ] <\displaystyle \rho (T)=\rho _<0>[1+\alpha (T-T_<0>)]>

Металлы [ править ]

В общем, удельное электрическое сопротивление металлов увеличивается с температурой. Электрон- фононные взаимодействия могут играть ключевую роль. При высоких температурах сопротивление металла линейно увеличивается с температурой. Когда температура металла понижается, температурная зависимость удельного сопротивления следует степенному закону функции температуры. Математически температурная зависимость удельного сопротивления металла ρ определяется формулой Блоха – Грюнайзена:

ρ ( T ) = ρ ( 0 ) + A ( T Θ R ) n ∫ 0 Θ R / T x n ( e x − 1 ) ( 1 − e − x ) d x <\displaystyle \rho (T)=\rho (0)+A\left(<\frac<\Theta _>>\right)^\int _<0>^<\Theta _/T><\frac ><(e^-1)(1-e^<-x>)>>\,dx>

Закон Видемана – Франца [ править ]

Закон Видемана – Франца гласит, что коэффициент электропроводности металлов при нормальных температурах обратно пропорционален температуре: [52]

При высоких температурах металла закон Видемана-Франца выполняется:

Полупроводники [ править ]

Еще лучшее приближение температурной зависимости удельного сопротивления полупроводника дается уравнением Стейнхарта – Харта :

1 T = A + B ln ⁡ ρ + C ( ln ⁡ ρ ) 3 <\displaystyle <\frac <1>>=A+B\ln \rho +C(\ln \rho )^<3>\,>

Внешние (легированные) полупроводники имеют гораздо более сложный температурный профиль. При повышении температуры, начиная с абсолютного нуля, их сопротивление сначала резко уменьшается, поскольку носители покидают доноры или акцепторы. После того, как большинство доноров или акцепторов потеряли своих носителей, сопротивление снова начинает немного увеличиваться из-за уменьшения подвижности носителей (как в металле). При более высоких температурах они ведут себя как собственные полупроводники, поскольку носители от доноров / акцепторов становятся незначительными по сравнению с носителями, генерируемыми термически. [53]

В некристаллических полупроводниках проводимость может происходить за счет квантового туннелирования зарядов из одного локализованного участка в другой. Это известно как скачкообразная перестройка диапазона и имеет характерную форму

где n = 2, 3, 4, в зависимости от размерности системы.

Комплексное сопротивление и проводимость [ править ]

Сопротивление в зависимости от удельного сопротивления в сложной геометрии [ править ]

В таких случаях формулы

должен быть заменен на

Произведение удельное сопротивление-плотность [ править ]

Серебро, хотя и является наименее резистивным из известных металлов, имеет высокую плотность и по своим характеристикам аналогично меди, но намного дороже. Кальций и щелочные металлы имеют лучшие произведения удельного сопротивления, но редко используются для проводников из-за их высокой реакционной способности с водой и кислородом (и отсутствия физической прочности). Алюминий гораздо более устойчив. Токсичность исключает выбор бериллия. [56] (Чистый бериллий также является хрупким). Таким образом, алюминий обычно является предпочтительным металлом, когда решающим фактором является вес или стоимость проводника.

Источник