Что называют траекторией в физике

Траектория

Кроме того, и при наличии движущегося по ней объекта, траектория, изображаемая в наперёд заданной системе пространственных координат, сама по себе не может ничего определённого сказать в отношении причин его движения, пока не проведён анализ конфигурации поля действующих на него сил в той же координатной системе. [2]

Не менее существенно, что форма траектории неотрывно связана и зависит от конкретной системы отсчёта, в которой описывается движение. [3]

Возможен и случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.

Содержание

Траектория свободной материальной точки

В соответствии с Первым законом Ньютона, иногда называемым законом инерции должна существовать такая система, в которой свободное тело сохраняет (как вектор) свою скорость. Такая система отсчёта называется инерциальной. Траекторией такого движения является прямая линия, а само движение называется равномерным и прямолинейным.

Описание траектории

Принято описывать траекторию материальной точки в наперёд заданной системе координат при помощи радиус-вектора, направление, длина и начальная точка которого зависят от времени. При этом кривая, описываемая концом радиус-вектора в пространстве может быть представлена в виде сопряжённых дуг различной кривизны, находящихся в общем случае в пересекающихся плоскостях. При этом кривизна каждой дуги определяется её радиусом кривизны, направленном к дуге из мгновенного центра поворота, находящегося в той же плоскости, что и сама дуга. При том прямая линия рассматривается как предельный случай кривой, радиус кривизны которой может считаться равным бесконечности. И потому траектория в общем случае может быть представлена как совокупность сопряжённых дуг.

Существенно, что форма траектории зависит от системы отсчёта, избранной для описания движения материальной точки. Так прямолинейное равномерно ускоряющееся движение в инерциальной системе в общем случае будет параболическим (до тех пор, пока набираемая скорость тела сравнима по величине со скоростью относительного движения равномерно двигающейся инерциальной системе отсчёта. См. Рисунок 2).

Связь со скоростью и нормальным ускорением

Скорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории точки. При этом существует связь между величиной скорости , нормальным ускорением и радиусом кривизны траектории в данной точке:

Однако, не всякое движение с известной скоростью по кривой известного радиуса и найденное по приведённой выше формуле нормальное (центростремительное) ускорение связано с проявлением силы, направленной по нормали к траектории (центростремительной силы). Так, найденное по данным фотографии суточного движения светил ускорение любой из звёзд отнюдь не говорит о существовании вызывающей это ускорение силы, притягивающей её к Полярной звезде, как центру вращения.

Связь с уравнениями динамики

Представление траектории как следа, оставляемого движением материальной точки, связывает чисто кинематическое понятие о траектории, как геометрической проблеме, с динамикой движения материальной точки, то есть проблемой определения причин её движения. Фактически, решение уравнений Ньютона (при наличии полного набора исходных данных) даёт траекторию материальной точки.

В соответствии с принципом относительности Галилея, существует бесконечное множество равноправных инерциальных систем (ИСО), движение которых одна относительно другой не может быть установлено никаким образом путём наблюдения любых процессов и явлений, происходящих только в этих системах. Прямая траектория равномерного движения объекта в одной системе будет выглядеть также прямой в любой другой инерциальной системе, хотя величина и направление скорости будут зависеть от выбора системы, то есть от величины и направления их относительной скорости.

Вместе с тем Принцип Галилея не утверждает, что одно и то же явление, наблюдаемое из двух разных ИСО, будут выглядеть одинаково. Поэтому Рис.2 предупреждает о двух типичных ошибках, связанных с забвением того, что:

1. Истинно, что любой вектор (в том числе вектор силы) может быть разложен по крайней мере на две составляющие. Но это разложение совершенно произвольно и не значит, что такие компоненты существуют в действительности. Для подтверждения их реальности должна привлекаться дополнительная информация, в любом случае не взятая из анализа формы траектории. Например, по рисунку 2 невозможно определить природу силы F, так же как невозможно утверждать, что она сама является или не является суммой сил разной природы. Можно лишь утверждать, что на изображённом участке она постоянна, и что для формирования наблюдаемой в данной СО криволинейности траектории служит вполне определённая в данной СО центростремительная часть этой силы. Зная лишь траекторию материальной точки в какой-либо инерциальной системе отсчёта и её скорость в каждый момент времени, нельзя определить природу сил, действовавших на неё.

2. Даже в случае наблюдения из ИСО, форма траектории ускоренно движущегося тела будет определяться не только действующими на него силами, но и выбором этой ИСО, никак на эти силы не влияющим. Центростремительная сила, показанная на рисунке 2, получена формально, и её величина непосредственно зависит от выбора ИСО.

Движение под действием внешних сил в инерциальной системе отсчёта

Если в заведомо инерциальной системе скорость движения объекта (для неподвижного в данной системе наблюдателя) с массой меняется по направлению, даже оставаясь прежней по величине, то есть тело производит поворот и движется по дуге с радиусом кривизны , то значит, это тело испытывает нормальное ускорение . Причиной, вызывающей это ускорение, является центростремительная сила, прямо пропорциональная этому ускорению. В этом состоит суть Второго закона Ньютона:

(1)

Где есть векторная сумма сил, действующих на тело, его ускорение, а — инерционная масса. [4]

В общем случае тело не бывает свободно в своём движении, и на его положение, а в некоторых случаях и на скорость, налагаются ограничения — связи. Если связи накладывают ограничения только на координаты тела, то такие связи называются геометрическими. Если же они распространяются и на скорости, то они называются кинематическими. Если уравнение связи может быть проинтегрировано во времени, то такая связь называется голономной.

Действие связей на систему движущихся тел описывается силами, называемыми реакциями связей. В таком случае сила, входящая в левую часть уравнения (1), есть векторная сумма активных (внешних) сил и реакции связей.

Существенно, что в случае голономных связей становится возможным описать движение механических систем в обобщённых координатах, входящих в уравнения Лагранжа. Число этих уравнений зависит лишь от числа степеней свободы системы и не зависит от количества входящих в систему тел, положение которых необходимо определять для полного описания движения.

Если же связи, действующие в системе идеальны, то есть в них не происходит переход энергии движения в другие виды энергии, то при решении уравнений Лагранжа автоматически исключаются все неизвестные реакции связей.

Наконец, если действующие силы принадлежат к классу потенциальных, то при соответствующем обобщении понятий становится возможным использования уравнений Лагранжа не только в механике, но и других областях физики. [5]

Действующие на материальную точку силы в этом понимании однозначно определяют форму траектории её движения (при известных начальных условиях). Обратное утверждение в общем случае не справедливо, поскольку одна и та же траектория может иметь место при различных комбинациях активных сил и реакций связи.

Движение под действием внешних сил в неинерциальной системе отсчёта

Иллюстрация

Но можно себе представить, что задачей рассматривающихся здесь коллег является именно нанесение прямой линии на вращающейся сцене. В этом случае нижний должен потребовать от верхнего движения по кривой, являющейся зеркальным отражением следа от ранее пролитой краски,оставаясь при этом над любой точкой прямой, проходящей в избранном радиальном направлении. Следовательно, прямолинейное движение в неинерциальной системе отсчёта не будет являться таковым для наблюдателя в инерциальной системе.

Более того, равномерное движение тела в одной системе, может быть неравномерным в другой. Так, две капли краски, упавшие в разные моменты времени из дырявого ведра, как в собственной системе отсчёта, так и в системе неподвижного по отношению к зданию нижнего коллеги (на уже прекратившей вращение сцене), будут двигаться по прямой (к центру Земли). Различие будет заключаться в том, что для нижнего наблюдателя это движение будет ускоренным, а для верхнего его коллеги, если он, оступившись, будет падать, двигаясь вместе с любой из капель, расстояние между каплями будет увеличиваться пропорционально первой степени времени, то есть взаимное движение капель и их наблюдателя в его ускоренной системе координат будет равномерным со скоростью , определяемой задержкой между моментами падения капель:

.

Где — ускорение свободного падения.

Поэтому форма траектории и скорость движения по ней тела, рассматриваемая в некоторой системе отсчёта, о которой заранее ничего не известно, не даёт однозначного представления о силах, действующих на тело. Решить вопрос о том, является ли эта система в достаточной степени инерциальной, можно лишь на основе анализа причин возникновения действующих сил.

Таким образом, в неинерциальной системе:

Примечания

Источник

ТРАЕКТОРИЯ (в физике)

Смотреть что такое «ТРАЕКТОРИЯ (в физике)» в других словарях:

Траектория — Рис.1 Траектории трёх объектов (угол запуска 70°, Distance расстояние, Height высота), разное лобовое сопротивление Запрос «Траектория» перенаправляется сюда; см. также другие значения. Траектория материальной точки линия … Википедия

Траектория материальной точки — Траектории трёх объектов (угол запуска 70°, Distance расстояние, Height высота), разное лобовое сопротивление Запрос «Траектория» перенаправляется сюда; см. также другие значения. Траектория материальной точки линия в… … Википедия

Важнейшие открытия в физике — История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия

СТАТИСТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАКОНОМЕРНОСТИ — две осн. формы закономерной связи явлений, которые отличаются по характеру вытекающих из них предсказаний. В законах динамич. типа предсказания имеют точно определённый, однозначный характер. Так, в механике, если известен закон движения… … Философская энциклопедия

Кибернетическая физика — Кибернетическая физика область науки на стыке кибернетики и физики, изучающая физические системы кибернетическими методами. Под кибернетическими методами понимаются методы решения задач управления, оценивания переменных и параметров… … Википедия

Действие (механика) — В физике принцип действия является утверждением о природе движения, из которого может быть определена траектория объекта, на который действуют внешние силы. Траектория объекта та, которая приводит к постоянному значению для физической величины,… … Википедия

Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия

ЭРГОДИЧЕСКАЯ ГИПОТЕЗА — в статистической физике, состоит в предположении, что средние по времени значения физ. величин, характеризующих систему, равны их средним статистич. значениям; служит для обоснования статистич. физики. Физ. системы, для к рых справедлива Э. г.,… … Физическая энциклопедия

Источник

Траектория движения тела

Траектория представляет собой своеобразный «след», который оставляет за собой движущееся тело в данной системе отсчета. Она позволяет наблюдателю этой системы отсчета увидеть все точки, которые последовательно проходило тело во время движения. Например, железнодорожный путь указывает траекторию движения поезда, автомобильное шоссе – траекторию движения автомашин. След, оставшийся в небе за летящим самолетом, «рисует» траекторию самолета, лыжня – траекторию лыжника, а любой текст, написанный на листе бумаги – траекторию кончика карандаша или ручки.

Траектория тела в разных системах отсчета

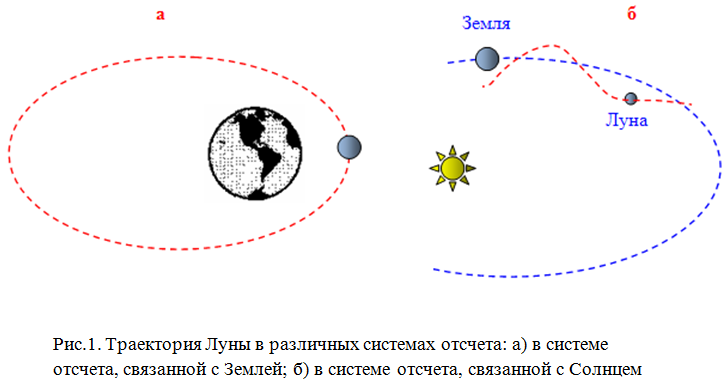
Следует отметить, что траектории движения одного и того же тела в разных системах отсчета могут быть различными. Например, в системе отсчета, связанной с Землей, траектория движения искусственного спутника вокруг Земли – окружность, а в системе отсчета, связанной с Солнцем, — винтовая линия или спираль (рис.1).

В зависимости от формы траектории механические движения делятся на прямолинейные (траектория – прямая линия) (рис.2, а) и криволинейные (траектория – кривая линия) (рис.2, б).

Определение уравнения траектории движения тела является одной из задач механики.

Примеры решения задач по теме «Траектория»

б) в системе отсчета, связанной с рамой, траектория точки обода вращающегося колеса – окружность, так как точка обода совершает вращательное движение относительно оси, закрепленной на раме;

в) в системе отсчета, связанной с землей, траектория точки обода вращающегося колеса – циклоида, потому что точка одновременно совершает поступательное и вращательное движения; длина дуги циклоиды равна длине окружности обода колеса.

Источник

Механическое движение и его характеристики

теория по физике 🧲 кинематика

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

По характеру движения точек тела выделяют три вида механического движения:

По типу линии, вдоль которой движется тело, выделяют два вида движения:

По скорости выделяют два вида движения:

По ускорению выделяют три вида движения:

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

Способы описания механического движения

Описать механическое движение можно двумя способами:

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

Перемещение

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет вид:

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

Точка В имеет координаты (5; 10).

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид :

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник