Что называют траекторией и какие траектории бывают
Траектория, длина пути, вектор перемещения
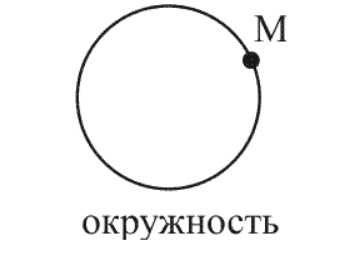
Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.
Виды движений тела
Существуют несколько видов движений и траекторий твердого тела:
Перемещение тела
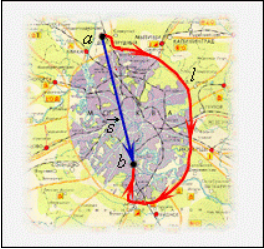
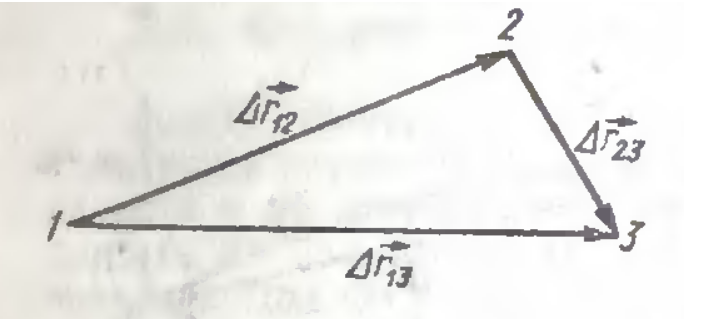
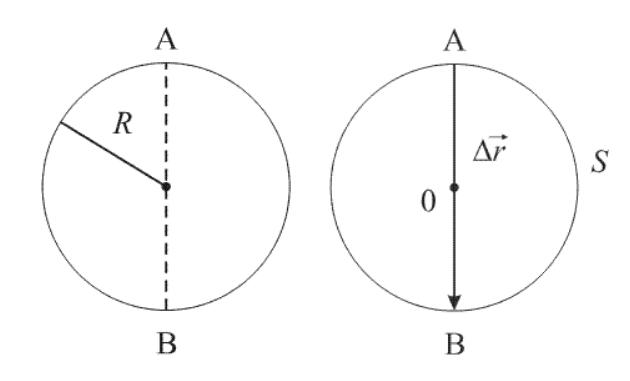
По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Перемещение принято считать векторной величиной. Этот отрезок имеет направление.
Путь – скалярная величина. Считается числом.
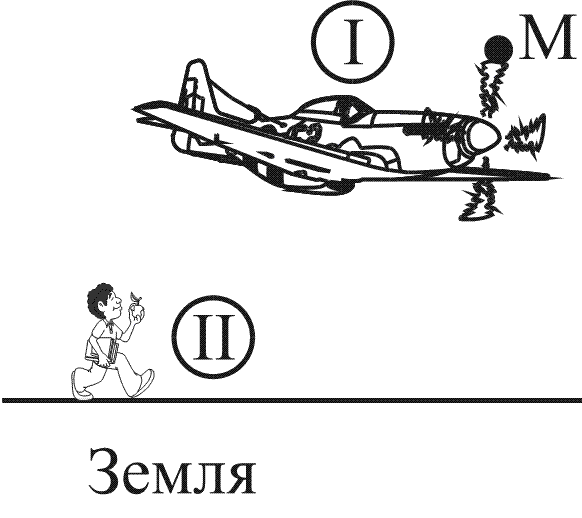
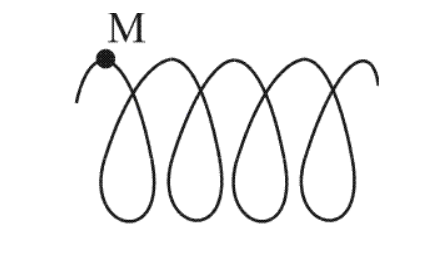
Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.
Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:
Подставляем числовые значения и получаем:
Траектория
Из Википедии — свободной энциклопедии
Траекто́рия материа́льной то́чки — линия в пространстве, по которой движется тело, и представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта. [1] Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.
Кроме того, и при наличии движущегося по ней объекта, траектория, изображаемая в наперёд заданной системе пространственных координат, сама по себе не может ничего определённого сказать в отношении причин его движения, пока не проведён анализ конфигурации поля действующих на него сил в той же координатной системе. [2]
Не менее существенно, что форма траектории неотрывно связана и зависит от конкретной системы отсчёта, в которой описывается движение. [3]
Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, звёздное небо может послужить хорошей моделью инерциальной и неподвижной системы отсчёта. Однако при длительной экспозиции эти звёзды представляются движущимися по круговым траекториям (Рис. 3)
Возможен и случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.
Траектория
Полезное
Смотреть что такое «Траектория» в других словарях:
ТРАЕКТОРИЯ — (от лат. trajicere перебрасывать, пересекать), в геометрии: прямая или кривая линия, которую описывает движущееся или падающее тело, напр., ядро, по выходе из пушки. 2) кривая, пересекающая систему однородных кривых под одним и тем же углом.… … Словарь иностранных слов русского языка
ТРАЕКТОРИЯ — (Trajectory) путь движения точки или тела, напр. траектория полета снаряда. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 Траектория непрерывная линия, описываемая в пространстве движуще … Морской словарь
ТРАЕКТОРИЯ — (от ср. век. лат. trajectorius относящийся к перемещению) линия, которую описывает точка при своем движении. Если траектория прямая линия, то движение называется прямолинейным, в противном случае криволинейным … Большой Энциклопедический словарь
ТРАЕКТОРИЯ — (от позднелат. trajectorius относящийся к перемещению), непрерывная линия, к рую описывает точка при своём движении. Если Т. прямая линия, движение точки наз. прямолинейным, в противном случае криволинейным. Вид Т. свободной материальной точки… … Физическая энциклопедия
траектория — орбита, путь, прохождение; глиссада, линия Словарь русских синонимов. траектория сущ., кол во синонимов: 3 • глиссада (3) • … Словарь синонимов
траектория — — [http://www.eionet.europa.eu/gemet/alphabetic?langcode=en] траектория Кривая, которую описывает точка при своем движении относительно выбранной системы координат. В экономико математические исследования этот термин вошел из аппарата… … Справочник технического переводчика
Траектория — (на средневековой латыни trajectorius относящийся к перемещению), линия, которую описывает материальная точка (или центр инерции твердого тела) при своем движении. Если траектория прямая линия, то движение называется прямолинейным, в противном… … Иллюстрированный энциклопедический словарь
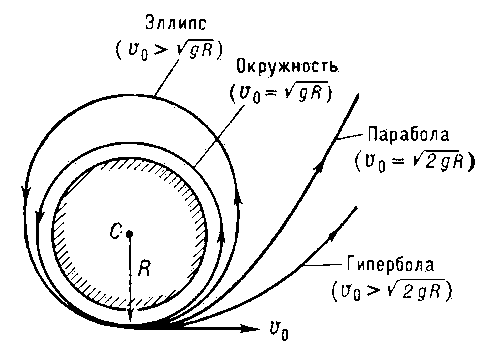
ТРАЕКТОРИЯ — ТРАЕКТОРИЯ, путь летящего тела. Если бы на Земле отсутствовало сопротивление воздуха, все траектории представляли бы собой отрезки ЭЛЛИПСА, один из фокусов которого находится в центре Земли. Поскольку радиус Земли составляет 6400 км, что, как… … Научно-технический энциклопедический словарь
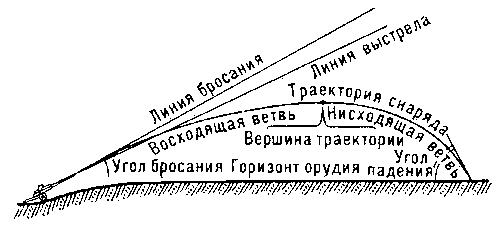
ТРАЕКТОРИЯ — ТРАЕКТОРИЯ, траектории, жен. (от лат. trajectus переброска). 1. Путь движения какого нибудь тела или точки (мат., физ.). Вычислить траекторию. 2. Кривая линия полета артиллерийского снаряда или пули (воен.). Толковый словарь Ушакова. Д.Н. Ушаков … Толковый словарь Ушакова
ТРАЕКТОРИЯ — ТРАЕКТОРИЯ, и, жен. (спец.). 1. Линия движения какого н. тела или точки. 2. Линия полёта пули, снаряда, ракеты. | прил. траекторный, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Значение слова «траектория»
[От лат. trajectus — передвижение, перемещение]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Кроме того, и при наличии движущегося по ней объекта, траектория, изображаемая в наперёд заданной системе пространственных координат, сама по себе не может ничего определённого сказать в отношении причин его движения, пока не проведён анализ конфигурации поля действующих на него сил в той же координатной системе.
Не менее существенно, что форма траектории неотрывно связана и зависит от конкретной системы отсчёта, в которой описывается движение.
Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, звёздное небо может послужить хорошей моделью инерциальной и неподвижной системы отсчёта. Однако при длительной экспозиции эти звёзды представляются движущимися по круговым траекториям (Рис. 3)
Возможен и случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.
ТРАЕКТО’РИЯ, и, ж. [от латин. trajectus — переброска]. 1. Путь движения какого-н. тела или точки (мат., физ.). Вычислить траекторию. 2. Кривая линия полета артиллерийского снаряда или пули (воен.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
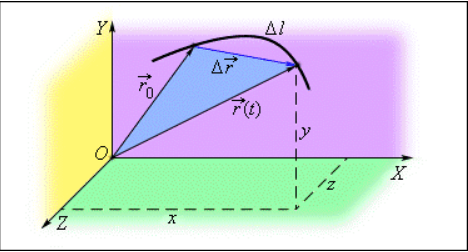
ТРАЕКТОРИЯ
— кривая, к-рую описывает радиус-вектор r(t )координат тела с течением времени (рис. 1). Понятие «Т.» тесно связано с понятиями «материальная точка» и «уравнения движения». Говорить о траектории имеет смысл лишь в том случае, когда размеры тела малы по сравнению с расстоянием, к-рое оно проходит.
Для определения ф-ции r(t) (а следовательно, и Т.) необходимо решить дифференц. ур-ние 2-го порядка, вытекающее из 2-го закона Ньютона:
Ур-ние (1) при заданной F определяет целое семейство траекторий. Выбор к.-л. одной из них осуществляется фиксацией нач. условий, роль к-рых обычно выполняют нач. координаты и скорость тела, Напр., подставляя в качестве силы F в ф-лу (1) силу всемирного тяготения,
В классич. механике, если известны координаты и скорость тела в к.-л. момент времени, то Т. движения [ф-ция r(t)]однозначно определяется законом движения (1).
Представление о Т. движения тела как о нек-рой гладкой кривой, к-рую можно найти, решив ур-ние (1), является чисто макроскопическим. Для микроскопич. тел это не так. Из основных постулатов термодинамики следует, что независимо от природы действующих на тело сил среднеквадратичная флуктуация скорости тела, находящегося в термодинамическом равновесии с внеш. средой, описывается ф-лой
Величина при комнатной темп-ре пренебрежимо мала для макроскопич. тел, но для отд. молекул она составляет уже неск. сотен м в секунду. Поэтому Т. движения микроскопич. тела будет представлять собой хаотическую ломаную линию, подобную изображённой на рис. 2. Это почти везде непрерывная и почти нигде недифференцируемая кривая. Она называется б р о у н о вс к о й т р а е к т о р и е й (см. Броуновское движение )и обладает тем свойством, что если увеличить любой её фрагмент, то мы увидим такую же кривую. Т., изображённая на рис. 2, является случайной, и имеет смысл говорить лишь о статистич. ансамбле таких Т. Полностью определёнными являются только средние по ансамблю величины. Напр., квадрат ср. смещения частицы 2 > как ф-ция времени t есть [А. Эйнштейн (A. Einstein), 1905]:
Броуновское движение является заданным, если известна ф-ция
к-рая имеет смысл вероятности того, что частица, находящаяся в точке r1 в момент времени t1 в момент t2 окажется в точке r2.
В простейшем случае одномерного броуновского движения ф-ция (5) имеет вид
Т. о., для микроскопии, тел Т. является статистич. понятием.
Для квантовых частиц понятие «Т.» утрачивает смысл. Количеств. критерием квантового движения является условие
«Увидеть» Т. движения квантовой частицы (напр., электрона в атоме) непосредственно при помощи микроскопа или попытаться «поймать» Т. к.-л. способом невозможно. С формальной точки зрения причина состоит в том, что в квантовой частице неприменимо понятие материальной точки, можно говорить лишь об амплитуде вероятности обнаружить частицу в том или ином состоянии. Как показал-Кйзенберг (1927), физ. причина такого положения вещей заключается в том, что, пытаясь измерить положение частицы, мы неизбежно воздействуем на неё, причём это воздействие не может быть меньше постоянной Планка. Следовательно, в квантовом случае [когда выполнено условие (7)] представление о Т. как о геом. месте точек, в каждой из к-рых частицы имеют определ. скорость, физически бессмысленно.
Несмотря на это, в 1947 Т. «вернулась» в квантовую механику благодаря остроумному формализму интегрирования по траекториям, разработанному Р. Фейнманом (R. P. Feynman), и, т. о., легла в основу его интерпретации квантовой механики (см. Фейнмана представление в квантовой механике).
Оказывается, амплитуда перехода квантовой частицы из точки r1,t1 в точку r2,t2 можно записать в виде
Ур-ние (1) определяет экстремальную Т. в интеграле (8), к-рую называют классич. Т.
Лит.: Винер Н., Нелинейные задачи в теории случайных процессов, пер. с англ., М., 1961; Фейнман Р. Ф., Хибс А. Р., Квантовая механика и интегралы по траекториям, пер. с англ., М., 1968; Сивухин Д. В., Общий курс физики, 3 изд., т. 1. Механика, М., 1989. М. А. Савров.