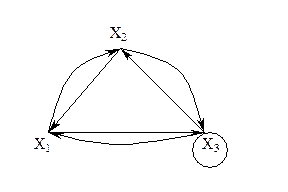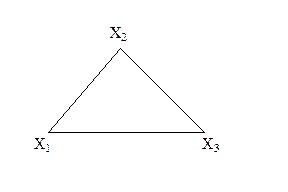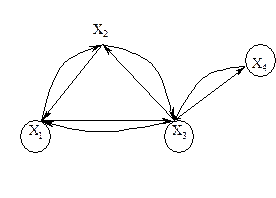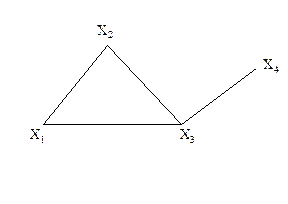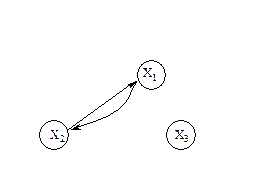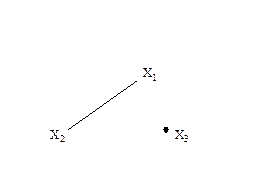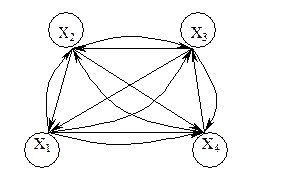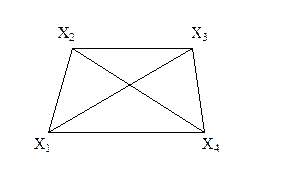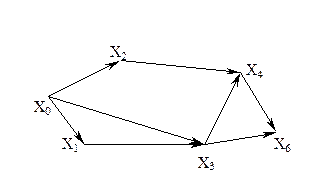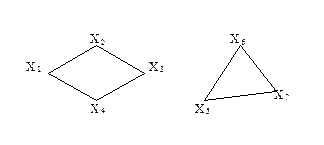Что называют степенью вершины графа
Степень вершины (теория графов)
Содержание
Лемма о рукопожатиях
По формуле суммы степеней для графа 
то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, формула утверждает, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях. Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других чётно.
Последовательность степеней вершин
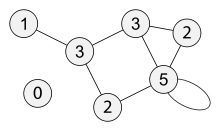
Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью. [2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристкой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.
Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence ). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.
Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность di (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство
Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, 2 или 4, но не при k равном 3.
С. Л. Хакими доказал, что (d1, d2, …, dn) есть последовательность степеней простого графа только если существует (d2 − 1, d3 − 1, …, dd1+1 − 1, dd1+2, dd1+3, …, dn). Этот факт позволил разработать простой алгоритм нахождения простого графа с заданной реализуемой последовательностью:
Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов.
Частные значения
Общие свойства
См. также
Примечания
Источники
Полезное
Смотреть что такое «Степень вершины (теория графов)» в других словарях:
Дуга (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Цикл (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Дерево (теория графов) — У этого термина существуют и другие значения, см. Дерево (значения). Дерево это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин, ацикличность отсутствие циклов и то, что между парами вершин… … Википедия
Графов теория — раздел конечной математики (См. Конечная математика), особенностью которого является геометрический подход к изучению объектов. Основное понятие теории граф. Граф задаётся множеством вершин (точек) и множеством рёбер (связей), соединяющих … Большая советская энциклопедия
Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия
Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия
Практическое применение раскраски графов — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Раскраска графов практически применяется (постановку задачи различиных раскрасок здесь обсуждаться не будет) дл … Википедия
Теоремы теории графов — Здесь собраны теоремы из теории графов. Содержание 1 Лемма о рукопожатиях 2 Существование эйлерова пути и цикла … Википедия
Вершина (граф) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Длина пути в орграфе — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Теория графов — основы
График — это диаграмма точек и линий, соединенных с точками. У него есть по крайней мере одна линия, соединяющая набор из двух вершин без вершин, соединяющих себя. Понятие графов в теории графов опирается на некоторые основные термины, такие как точка, линия, вершина, ребро, степень вершин, свойства графов и т. Д. Здесь, в этой главе, мы рассмотрим эти основы теории графов.
точка
Точка — это конкретная позиция в одномерном, двухмерном или трехмерном пространстве. Для лучшего понимания точку можно обозначить алфавитом. Его можно обозначить точкой.
пример
Здесь точка — это точка с именем «а».
Линия
Линия — это связь между двумя точками. Это может быть представлено сплошной линией.
пример
Здесь «а» и «б» являются точками. Связь между этими двумя точками называется линией.
пример
Здесь вершина названа с алфавитом «а».
Ребро — это математический термин для линии, соединяющей две вершины. Многие ребра могут быть сформированы из одной вершины. Без вершины ребро не может быть сформировано. Для ребра должна быть начальная и конечная вершина.
пример
Здесь «a» и «b» — две вершины, и связь между ними называется ребром.
график
Граф ‘G’ определяется как G = (V, E), где V — множество всех вершин, а E — множество всех ребер графа.
Пример 1
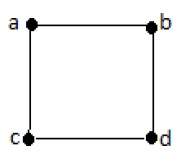
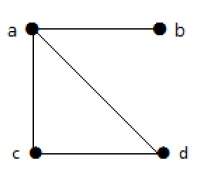
В приведенном выше примере ab, ac, cd и bd являются ребрами графа. Аналогично, a, b, c и d являются вершинами графа.
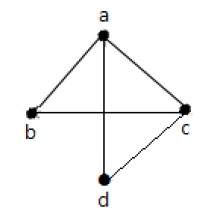
Пример 2
В этом графе есть четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.
петля
В графе, если ребро нарисовано от вершины к себе, это называется циклом.
Пример 1
На приведенном выше графике V — вершина, для которой у нее есть ребро (V, V), образующее петлю.
Пример 2
В этом графе есть две петли, которые сформированы в вершине a, и вершине b.
Степень вершины
Это число вершин, смежных с вершиной V.
Обозначение — град (V).
В простом графе с n числом вершин степень любых вершин равна —
Степень вершины можно рассматривать по двум случаям графов —
Степень вершины в неориентированном графе
Ненаправленный граф не имеет направленных ребер. Рассмотрим следующие примеры.
Пример 1
Посмотрите на следующий график —
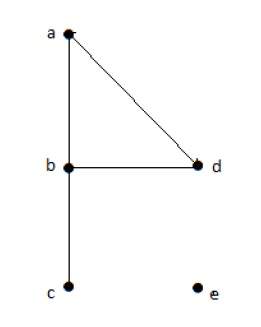
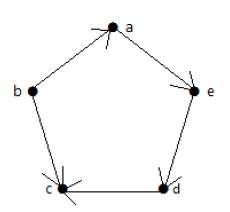
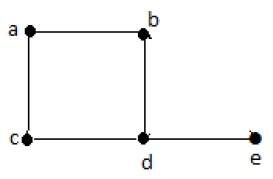
На приведенном выше неориентированном графике
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
Пример 2
Посмотрите на следующий график —
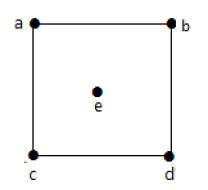
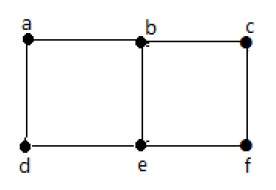
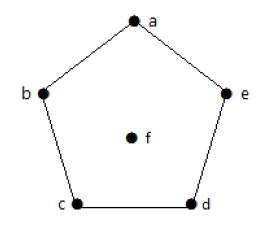
На приведенном выше графике
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.
Вершина «е» является изолированной вершиной. Граф не имеет никакой вершины.
Степень вершины в ориентированном графе
В ориентированном графе каждая вершина имеет степень и степень.
Степень графа
Степень вершины V — это количество ребер, входящих в вершину V.
Обозначение — град — (V).
Степень вершины V — это количество ребер, входящих в вершину V.
Обозначение — град — (V).
Степень графа
Отступ вершины V — это число ребер, выходящих из вершины V.
Обозначение — град + (V).
Отступ вершины V — это число ребер, выходящих из вершины V.
Обозначение — град + (V).
Рассмотрим следующие примеры.
Пример 1
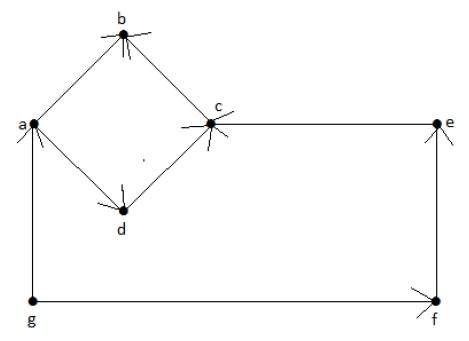
Посмотрите на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые идут наружу. Следовательно, его степень равна 2. Аналогично, существует ребро «ga», идущее к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 2 | |
| б | 2 | 0 |
| с | 2 | 1 |
| d | 1 | 1 |
| е | 1 | 1 |
| е | 1 | 1 |
| г | 0 | 2 |
Пример 2
Посмотрите на следующий ориентированный граф. Вершина ‘a’ имеет ребро ‘ae’, идущее наружу от вершины ‘a’. Следовательно, его степень равна 1. Аналогично, у графа есть ребро «ba», приближающееся к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 1 | |
| б | 0 | 2 |
| с | 2 | 0 |
| d | 1 | 1 |
| е | 1 | 1 |
Кулон Вертекс
Используя степень вершины, мы получаем два специальных типа вершин. Вершина с первой степенью называется нерешенной вершиной.
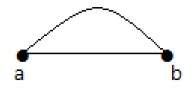
пример
Здесь, в этом примере, вершина ‘a’ и вершина ‘b’ имеют соединенное ребро ‘ab’. Таким образом, что касается вершины «a», то к вершине «b» имеется только одно ребро, и аналогично по отношению к вершине «b» есть только одно ребро к вершине «a». Наконец, вершина ‘a’ и вершина ‘b’ имеют степень как единицу, которая также называется висячей вершиной.
Изолированная вершина
Вершина с нулевой степенью называется изолированной вершиной.
пример
Здесь вершина «a» и вершина «b» не имеют связи между собой, а также с любыми другими вершинами. Таким образом, степень обеих вершин ‘a’ и ‘b’ равна нулю. Они также называются изолированными вершинами.
смежность
Вот нормы смежности —
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
Пример 1
На приведенном выше графике —
«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
Пример 2
На приведенном выше графике —
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
Параллельные края
В графе, если пара вершин соединена более чем одним ребром, то эти ребра называются параллельными ребрами.
На приведенном выше графике «a» и «b» — это две вершины, которые соединены между собой двумя ребрами «ab» и «ab». Так это называется параллельным ребром.
Мульти График
Граф, имеющий параллельные ребра, называется мультиграфом.
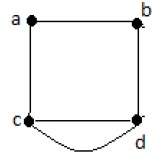
Пример 1
На приведенном выше графике есть пять ребер «ab», «ac», «cd», «cd» и «bd». Поскольку ‘c’ и ‘d’ имеют два параллельных ребра между ними, это мультиграф.
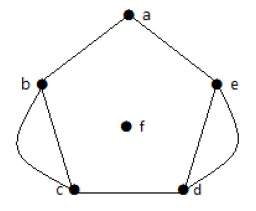
Пример 2
На приведенном выше графике вершины «b» и «c» имеют два ребра. Вершины ‘e’ и ‘d’ также имеют два ребра между ними. Следовательно, это мультиграф.
Степень последовательности графика
Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью графа графа.
Пример 1
| темя | б | с | d | е | |
|---|---|---|---|---|---|
| Присоединенный к | До нашей эры | объявление | объявление | с, Ь, е | d |
| степень | 2 | 2 | 2 | 3 | 1 |
На приведенном выше графике для вершин
Пример 2
| темя | б | с | d | е | е | |
|---|---|---|---|---|---|---|
| Присоединенный к | быть | а, с | б, г | с, е | объявление | — |
| степень | 2 | 2 | 2 | 2 | 2 | 0 |
На приведенном выше графике для вершин
Степень вершины графа. Число ребер графа



Вершина Xi называется инцидентной дуге (ребру) графа, если она является началом или концом этой дуги (ребра).
Степенью вершины графа называют число дуг (ребер), инцидентных данной вершине. Степень обозначается P(Xi).
Граф, изображенный на рис. 3.1.2, имеет один вход – вершину X0
Число ребер графа N связано со степенями его вершин следующим соотношением:
N= 
где n – число вершин графа. Отсюда следует справедливость следующих утверждений:
1) Сумма степеней вершин любого графа четна;
2) Для любого графа число вершин, имеющих нечетные степени, четно;
3) Для однородного графа, т.е. графа, все степени вершин которого одинаковы и равны r, N= 
4) Для полного графа, т.е. графа, в котором каждая пара вершин соединена ребром или дугой, P(Xi)=n-1, а N= 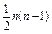
Некоторой противоположностью полному графу является нуль-граф, не имеющий ребер или дуг и состоящий из изолированных вершин. Очевидно, степени вершины нуль-графа равны 0.
Связность
Граф называется связным, если множество его вершин нельзя разбить на два или более подмножеств так, чтобы ни одна вершина одного подмножества не отображалась в вершину другого. В противном случае граф называется несвязным. Число подмножеств, не связанных отображениями, на которое разбивается множество всех вершин графа, называется числом компонент связности для несвязного графа.
Существует другое определение связности графа. Граф называется связным, если две любые его вершины можно соединить цепью. Граф (рис. 3.1.3) является несвязным с двумя компонентами связности.
Ребро графа называется перешейком, или связующей линией, если его удаление приводит к тому, что граф становится несвязным. На рис. 3.1.4 изображены три связных неориентированных графа, причем граф 1 не имеет ни одного перешейка, 2 содержит один перешеек (отмечен жирной линией), граф 3 целиком состоит из одних перешейков. Такой граф (3) называется деревом.
Степень вершины графа. Число ребер графа.
Теория графов
Графы
X=
Общепринято обозначать орграфы в виде
X – множество вершин орграфа;
U – множество дуг орграфа, или в виде
ГX = <Гx1,Гx2,…,Гxn> – множество образов элементов множества X, т.е. отображение X в X, понимая термин отображения как точечно-множественное отображение.
Две вершины графа называются смежными, если они соединены с началом другой.
Дуги называются смежными, если конец одной из них совпадает с началом другой.
Некоторая последовательности смежных дуг называется путем, а последовательность смежных ребер называется цепью.
Замкнутый путь называется контуром, а замкнутая цепь – циклом.
Сформулированные определения удобно представить в виде следующей таблицы:
| Ориентированный граф | Неориентированный граф |
| Дуга | Ребро |
| Путь | Цепь |
| Контур | Цикл |
Рассмотрим еще некоторые определения, которые нам понадобятся в дальнейшем. Пусть (цепь) называется элементарным, если он проходит через вершины графа по одному разу.
Путь (цепь) называется простым, если он проходит через дуги графа по одному разу. В противном случае путь (цепь) называется составным. Аналогично определяются и простые контуры и циклы.
Цепь (цикл) называется гамильтоновой, если она проходит через все вершины графа по одному разу, т.е. элементарная цепь, проходящая через все вершины графа, есть гамильтонова цепь.
Цепь (цикл) называется эйлеровой, если она проходит через все ребра по одному разу, т.е. простая цепь (цикл), содержащая все ребра графа есть эйлерова цепь (цикл).
Аналогично определяются гамильтоновы и эйлеровы путь и контуры.
Симметричный граф Неориентированный граф
Граф-толерантность Неориентированный граф
Граф-толерантность Неориентированный граф
Граф-декартово произведение Неориентированный полный граф
(с полным насыщением)
Степень вершины графа. Число ребер графа.
Вершина Xi называется инцидентной дуге (ребру) графа, если она является началом или концом этой дуги (ребра).
Степенью вершины графа называют число дуг (ребер), инцидентных данной вершине. Степень обозначается P(Xi).
Граф, изображенный на рис. 3.1.2, имеет один вход – вершину X0
Число ребер графа N связано со степенями его вершин следующим соотношением:
N= 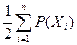
где n – число вершин графа. Отсюда следует справедливость следующих утверждений:
1) Сумма степеней вершин любого графа четна;
2) Для любого графа число вершин, имеющих нечетные степени, четно;
3) Для однородного графа, т.е. графа, все степени вершин которого одинаковы и равны r, N= 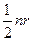
4) Для полного графа, т.е. графа, в котором каждая пара вершин соединена ребром или дугой, P(Xi)=n-1, а N= 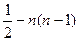
Некоторой противоположностью полному графу является нуль-граф, не имеющий ребер или дуг и состоящий из изолированных вершин. Очевидно, степени верши нуль-графа равны 0.
Связность
Граф называется связным, если множество его вершин нельзя разбить на два или более подмножеств так, чтобы ни одна вершины одного подмножества не отображалась в вершину другого. В противном случае граф называется несвязным. Число подмножеств всех вершин графа, называется числом компонент связности для несвязного графа.
Существует другое определение связности графа. Граф называется связным, если две любые его вершины можно соединить цепью. Граф (рис. 3.1.3) является несвязным с двумя компонентами.
Ребро графа называется перешейком, или связующей линией, если его удаление приводит к тому, что граф становится несвязным. На рис. 3.1.4 изображены три связных неориентированных графа, причем граф 1 не имеет ни одного перешейка, 2 содержит один перешеек (отмечен жирной линией), граф 3 целиком состоит из одних перешейков. Такой граф (3) называется деревом.