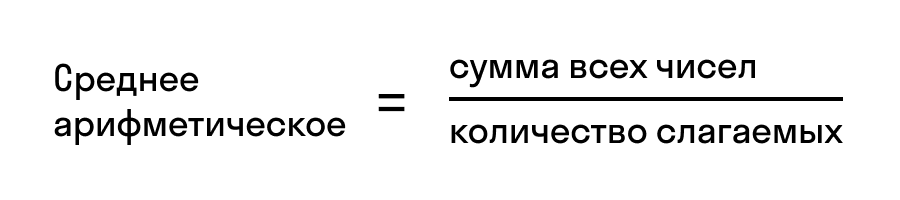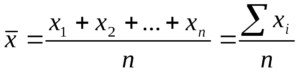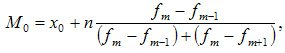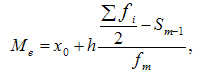Что называют средним арифметическим ряда чисел найдите среднее арифметическое ряда чисел 5555555
Что называют средним арифметическим ряда чисел найдите среднее арифметическое ряда чисел 5555555
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Для ряда a1,a1. an среднее арифметическое вычисляется по формуле:
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.
3 простых формулы, чтобы посчитать среднее арифметическое
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Вот так:
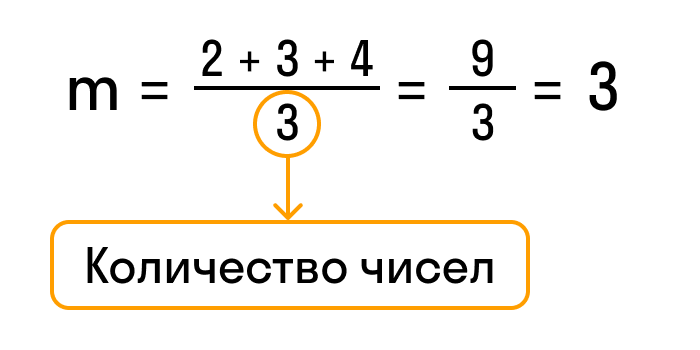
Например, найдем среднее арифметическое чисел 5, 6 и 7. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на три.
Так получилась формула среднего арифметического:
Способы вычисления среднего арифметического
Стандартная формула. Чтобы найти среднее арифметическое, нужно сложить все числа и поделить эту сумму на их количество. Формула выглядит так:
Вычисление моды или наиболее часто встречающегося значения. Формула такая:
Вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. Если такого значения нет, за медиану принимают среднее число между границами половин выборки. Формула выглядит так:
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: в магазине, на работе, в диалоге с другом или во время презентации перед инвесторами. Еще пригодятся, чтобы рассчитать среднюю скорость движения.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Посчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
В 5 классе можно искать среднее арифметическое с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Что называют средним арифметическим ряда чисел найдите среднее арифметическое ряда чисел 5555555
Среднее арифметическое ряда чисел – это сумма данных чисел, поделенная на количество слагаемых.
Среднее арифметическое называют средним значением числового ряда.
Пример : Найдем среднее арифметическое чисел 2, 6, 9, 15.
Решение. У нас четыре числа. Значит, надо их сумму разделить на 4. Это и будет среднее арифметическое данных чисел:
(2 + 6 + 9 + 15) : 4 = 8.
Среднее геометрическое ряда чисел – это корень n-й степени из произведения этих чисел.
Пример : Найдем среднее геометрическое чисел 2, 4, 8.
Решение. У нас три числа. Значит, надо найти корень третьей степени из их произведения. Это и будет среднее геометрическое данных чисел:
3 √ 2 · 4 · 8 = 3 √64 = 4
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Пример : Найти размах чисел 2, 5, 8, 12, 33.
Решение : Наибольшее число здесь 33, наименьшее 2. Значит, размах составляет 31:
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Пример : Найти моду ряда чисел 1, 7, 3, 8, 7, 12, 22, 7, 11, 22, 8.
Решение : Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медиана.
В упорядоченном ряде чисел:
Медиана нечетного количества чисел – это число, записанное посередине.
Пример : В ряде чисел 2, 5, 9, 15, 21 медианой является число 9, находящееся посередине.
Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Пример : Найти медиану чисел 4, 5, 7, 11, 13, 19.
Решение : Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел:
Число 9 и является медианой данного ряда чисел.
В неупорядоченном ряде чисел:
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Пример 1 : Найдем медиану произвольного ряда чисел 5, 1, 3, 25, 19, 17, 21.
Решение : Располагаем числа в порядке возрастания:
1, 3, 5, 17, 19, 21, 25.
Посередине оказывается число 17. Оно и является медианой данного ряда чисел.
Пример 2 : Добавим к нашему произвольному ряду чисел еще одно число, чтобы ряд стал четным, и найдем медиану:
5, 1, 3, 25, 19, 17, 21, 19.
Решение : Снова выстраиваем упорядоченный ряд:
1, 3, 5, 17, 19, 19, 21, 25.
Посередине оказались числа 17 и 19. Находим их среднее значение:
Число 18 и является медианой данного ряда чисел.
Среднее арифметическое чисел. Мода. Медиана. Размах ряда чисел
Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Например: найдем среднее арифметическое чисел 2; 6; 9; 15.
У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Например: найдем размах чисел 2; 5; 8; 12; 33.
Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.
Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.
Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.
Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.
В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.
Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите медиану и размах ряда.
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите моду ряда и среднее арифметическое ряда.
Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.
Найдите среднюю заработную плату.
Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.
Найдите разность среднего арифметического и медианы этого набора.
Найдите объем и медиану числового ряда.
Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:
| I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|
| 37 | 34 | 35 | 32 | 36 | 33 | 38 |
Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.
Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.
Найдите среднее арифметическое этого набора чисел.
Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.
Найдите медиану этого набора чисел.
Провели несколько измерений случайной величины:
800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.
Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.
Найдите разность среднего арифметического и медианы этого набора.
Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.
Найдите среднее арифметическое, размах и моду.
Как находить и вычислять для двух среднее арифметическое значение
Под понятием среднего арифметического чисел подразумевается результат несложной последовательности расчётов средней величины для ряда чисел, определённых заранее. Необходимо отметить, что такое значение в данное время широко применяется специалистами ряда отраслей. Например, известны формулы при проведении расчётов экономистами или работниками статистической отрасли, где требуется иметь значение данного типа. Кроме этого, этот показатель активно используют и в ряде других отраслей, которые являются смежными с вышеуказанными.
Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сможет любой желающий. Для этого не надо иметь специальное образование. Часто нет необходимости применять и вычислительную технику.
В качестве ответа на вопрос как найти среднее арифметическое рассмотрим ряд ситуаций.
Подсчёт среднего арифметического пары
Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:
Формула
Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:
В этой формуле применяется следующее обозначение:
А и В – это заранее выбранные числа, для которых необходимо находить значение.
Нахождение значения для трёх
Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:
Формула
Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:
В данной формуле принято следующее обозначение:
А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.
Вычисление среднего арифметического четырёх
Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:
Формула
Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:
В данной формуле переменные имеют следующее значение:
А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.
Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.
Подсчёт среднего арифметического пяти
Выполнение данной операции потребует проведения определённого алгоритма действий.
Формула
Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:
В данной формуле переменные имеют такое обозначение:
А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.
Универсальная формула вычисления
Проводя рассмотрение различных вариантов формул для вычисления среднего арифметического, можно обратить внимание на то, что у них есть общая закономерность.
Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.
Главным при определении формулы является принцип расчёта среднего арифметического.
Данный принцип как было видно из приведённых примеров, выглядит таким образом:
Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:
(А+В+…+N)/N
Данная формула содержит следующие переменные:
А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.
N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.
Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.
Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.
Видео
Из видео вы узнаете, как находить среднее арифметическое.