Шкала измерительного прибора, цена деления шкалы

Шкала — плоская или цилиндрическая поверхность, относительно которой движется стрелка, на которой нанесены деления.

Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка. Давайте же разберемся, что это за шкалы, и как ими пользоваться, чтобы ничего не напутать.

Для начала отметим, что шкалы эти бывают разными. Во-первых, более распространенными являются именованные шкалы, то есть шкалы, на которых деления проградуированы соответствующими единицами измеряемых величин, это градуированные шкалы.

Во-вторых, встречаются условные шкалы. Если прибор имеет несколько переключаемых пределов измерений, то шкала будет наверняка условной, и одни и те же деления будут иметь разные значения в каждом из установленных пользователем пределов.

Для того, чтобы по условной шкале прибора определить точно значение измеряемой в данный момент величины, необходимо, зная цену деления, количество делений до того места, куда отклонилась, и где остановилась в данный момент стрелка, умножить на цену деления.

Если цена деления не ясна, то ее можно легко найти, для этого берется разность между двумя известными значениями на шкале, и делится на количество делений между этими значениями. Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.

Если на шкале есть отметка ноль, то шкала называется нулевой. Если нуля нет, то шкала называется безнулевой. Что касается нулевых шкал, то они, в свою очередь, подразделяются на односторонние и двухсторонние. На фото выше можно видеть сразу семь нулевых шкал.

У односторонних ноль размещен в самом начале шкалы (как на рисунке, головка вольтметра с односторонней шкалой), а у двухсторонних — по центру или между конечной и начальной отметками. Так, в зависимости от расположения нуля, двухсторонние шкалы подразделяются на несимметричные и симметричные.

Симметричная шкала ноль имеет по центру, несимметричная — не по центру шкалы. Если шкала безнулевая, то крайние отметки обозначают верхний и нижний пределы измерений. На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.

В зависимости от характера связи угловых и линейных расстояний между двумя соседними делениями шкалы с измеряемыми величинами, шкалы бывают неравномерными, равномерными, логарифмическими, степенными и т. д. Для более точных измерений предпочтительней равномерные шкалы.

Когда отношение ширины самого широкого деления к самому узкому не более 1,3 при неизменной цене деления, шкалу уже можно считать равномерной.

На лицевой стороне измерительного прибора, недалеко от шкалы, как правило, размещены необходимые маркировки: единица величины измерения, ГОСТ, класс точности прибора, число фаз и род тока, категория защищенности данного измерительного прибора от внешних электрических и магнитных полей, условия эксплуатации, рабочее положение, предельное напряжение прочности изоляции измерительных цепей (на фото — в звездочке «2», значит 2 кВ), номинальная частота тока, если отличается от промышленных 50 Гц, например 500 Гц, положение относительно Земли, тип, система прибора, год выпуска, заводской номер, и прочие важные параметры.

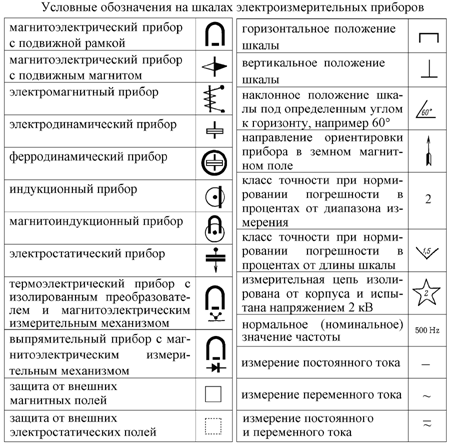
В этой таблице приведены расшифровки основных обозначений, которые можно встретить на шкалах. Надеемся, что эта краткая статья поможет вам научиться правильно проводить измерения при помощи стрелочных измерительных приборов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Погрешности измерений, представление результатов эксперимента

п.1. Шкала измерительного прибора

Примеры шкал различных приборов:

Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Пример определения цены деления:

Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: \begin \triangle=\frac\\ \triangle=\frac<10-5><24+1>=\frac15=0,2\ c \end

п.3. Виды измерений

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Определяется субъективным фактором, ошибками экспериментатора.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

Пример получения результатов прямых измерений с помощью линейки:

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

Сначала находим среднее значение всех измерений: \begin m_0=\frac<99,8+101,2+100,3><3>=\frac<301,3><3>\approx 100,4\ \text <г>\end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin \triangle_1=|100,4-99,8|=0,6\\ \triangle_2=|100,4-101,2|=0,8\\ \triangle_3=|100,4-100,3|=0,1 \end Находим среднее абсолютное отклонение: \begin \triangle_=\frac<0,6+0,8+0,1><3>=\frac<1,5><3>=0,5\ \text <(г)>\end Мы видим, что полученное значение \(\triangle_\) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: \begin \triangle m=max\left\<\triangle_; d\right\>=max\left\<0,5; 0,05\right\>\ \text <(г)>\end Записываем результат: \begin m=m_0\pm\triangle m\\ m=(100,4\pm 0,5)\ \text <(г)>\end Относительная погрешность (с двумя значащими цифрами): \begin \delta_m=\frac<0,5><100,4>\cdot 100\text<%>\approx 0,050\text <%>\end

п.6. Представление результатов эксперимента

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Мерой точности является относительная погрешность измерений. Получаем: \begin \delta_1=\frac<0,1><4,0>\cdot 100\text<%>=2,5\text<%>\\ \delta_2=\frac<0,03><4,0>\cdot 100\text<%>=0,75\text <%>\end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Источник

Классификация электроизмерительных приборов, условные обозначения на шкалах приборов

Для контроля за правильностью работы электротехнических установок, испытания их, определения параметров электрических цепей, учета расходуемой электрической энергии и т. д. производят различные электрические измерения. В технике связи, как и в технике сильных токов, электрические измерения имеют важное значение. Приборы, с помощью которых измеряются различные электрические величины: ток, напряжение, сопротивление, мощность и т. д., — называются электрическими измерительными приборами.

Существуют большое количество различных электроизмерительных приборов. Наиболее часто при производстве электрических измерений используются: амперметры, вольтметры, гальванометры, ваттметры, электросчетчики, фазометры, фазоуказатели, синхроноскопы, частотомеры, омметры, мегомметры, измерители сопротивления заземления, измерители емкости и индуктивности, осциллографы, измерительные мосты, комбинированные приборы и измерительные комплекты.

Классификация электроизмерительных приборов по принципу действия

По принципу действия электроизмерительные приборы подразделяются на следующие основные типы:

По типу отсчетного устройства различают аналоговые и цифровые приборы. В аналоговых приборах измеряемая или пропорциональная ей величина непосредственно воздействует на положение подвижной части, на которой расположено отсчетное устройство. В цифровых приборах подвижная часть отсутствует, а измеряемая или пропорциональная ей величина преобразуется в числовой эквивалент, регистрируемый цифровым индикатором.

Индукционный счетчик электроэнергии:

Отклонение подвижной части у большинства электроизмерительных механизмов зависит от значений токов в их катушках. Но в тех случаях, когда механизм должен служить для измерения величины, не являющейся прямой функцией тока (сопротивления, индуктивности, емкости, сдвига фаз, частоты и т. д.), необходимо сделать результирующий вращающий момент зависящим от измеряемой величины и не зависящим от напряжения источника питания.

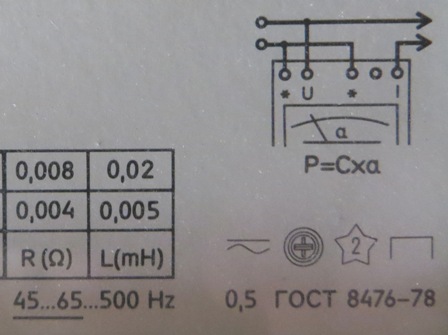
Условные обозначения на вольтметре:

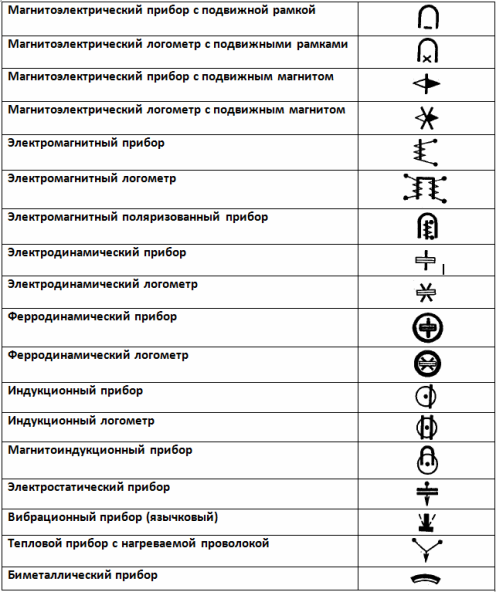
На рисунках ниже приведены условные обозначения электроизмерительных приборов по принципу их действия.

Обозначение принципа действия прибора

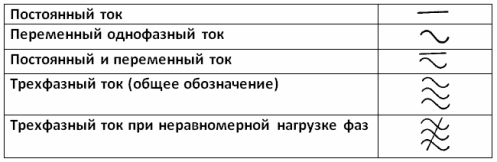
Обозначения рода тока

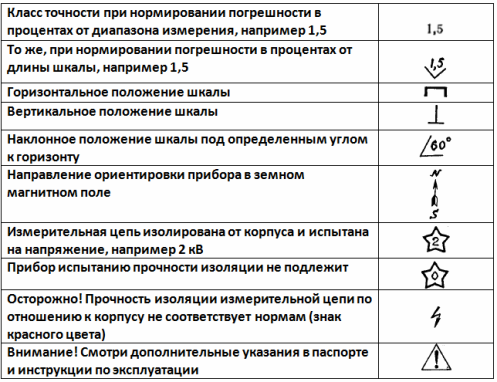
Обозначения класса точности, положения прибора, прочности изоляции, влияющих величин

Классификация электроизмерительных приборов по роду измеримой величины

Электроизмерительные приборы классифицируются и по роду измеряемой ими величины, так как приборы одного и того же принципа действия, но предназначенные для измерения разных величин могут значительно отличаться друг от друга по своей конструкции, не говоря уже о шкале прибора.

В таблице 1 приведен перечень условных обозначений наиболее употребительных электроизмерительных приборов.

Таблица 1. Примеры обозначения единиц измерения, их кратных и дольных значений

Классификация электроизмерительных приборов по степени точности

Абсолютной погрешностью прибора называют разность между показанием прибора и истинным значением измеряемой величины.

Например, абсолютная погрешность амперметра равна

Если I > I э, то абсолютная погрешность прибора положительна, а при I э, она отрицательна.

Поправкой прибора называют величину, которую надо прибавить к показаниям прибора, чтобы получить истинное значение измеряемой величины.

Приведенной погрешностью прибора называется отношение абсолютной погрешности к наибольшему возможному отклонению показателя прибора (номинальному показанию прибора).

Например, для амперметра

Точность прибора характеризуется величиной его максимальной приведенной погрешности. Согласно ГОСТ 8.401-80 приборы по степени их точности разделяются на 9 классов: 0,02, 0,05, 0,1, 0,2, 0,5, 1,0, 1,5, 2,5 и 4,0. Если, например, данный прибор имеет класс точности 1,5, то это значит, что его максимальная приведенная погрешность равна 1,5%.

Электроизмерительные приборы, имеющие классы точности 0,02, 0,05, 0,1 и 0,2, как наиболее точные, применяются там, где требуется весьма большая точность измерения. Если прибор имеет приведенную погрешность выше 4%, то он считается внеклассным.

Прибор для измерения угла сдвига фаз с классом точности 2,5:

Чувствительность и постоянная измерительного прибора

Чувствительностью прибора называют отношение углового или линейного перемещения указателя прибора, приходящееся на единицу измеряемой величины. Если шкала прибора равномерна, то чувствительность его по всей шкале одинакова.

Например, чувствительность амперметра, имеющего равномерную шкалу, определяется формулой

Если шкала прибора неравномерна, то чувствительность прибора в различных областях шкалы различна, так как одному и тому же приращению (например, тока) будут соответствовать разные приращения углового или линейного перемещения показателя прибора.

Величина, обратная чувствительности прибора, называется постоянной прибора. Следовательно, постоянная прибора — это цена деления прибора, или, иначе, величина, на которую должен быть помножен отсчет по шкале в делениях, чтобы получить измеряемую величину.

Например, если постоянная прибора равна 10 мА/дел (десять миллиампер на деление), то при отклонении его указателя на α = 10 делений измеряемая величина тока равна I = 10 · 10 = 100 мА.

Калибровка измерительных приборов — определение погрешностей или поправок для совокупности значений шкалы прибора путем сравнения в различных сочетаниях отдельных значений шкалы друг с другом. За основу сравнения берется одно из значений шкалы. Калибровка широко применяется в практике точной метрологической работы.

Простейший способ калибровкой — сравнение каждого размера с номинально равным ему (принимаемым за достаточно верный) размером. Это понятие не следует смешивать (как это часто делают) с градуированием (градуировкой) измерительных приборов, представляющим собой метрологическую операцию, при помощи которой делениям шкалы измерительного прибора придаются значения, выраженные в установленных единицах измерения.

Мощность потерь энергии в приборах

Электроизмерительные приборы потребляют при работе энергию, которая в них преобразуется обычно в тепловую энергию. Мощность потерь зависит от режима в цепи, а также от системы и конструкции прибора.

Если измеряемая мощность относительно мала, а следовательно, относительно малы ток или напряжение в цепи, то мощность потерь энергии в самих приборах может заметно влиять на режим исследуемой цепи и показания приборов могут иметь довольно большую погрешность. При точных измерениях в цепях, где развиваемые мощности сравнительно малы, необходимо знать мощность потерь энергии в приборах.

В табл. 2 приведены средние величины мощности потерь энергии в различных системах электроизмерительных приборов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник