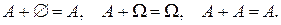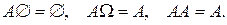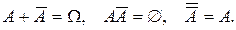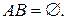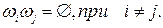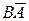Что называют разностью двух событий
Операции над событиями
Виды случайных событий
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Пример 1.10. Из ящика с деталями наугад извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События <появилась стандартная деталь>и <появилась нестандартная деталь>—несовместные.
Пример 1.11. Брошена монета. Появление «герба» исключает появление цифры. События <появился герб>и <появилась цифра>— несовместные.
Несколько событий образуют полную группу, если в результате испытания появится, хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Этот частный случай представляет для нас наибольший интерес, поскольку используется далее.
Пример 1.12. Приобретены два билета денежно-вещевой лотереи. Обязательно произойдет одно и только одно из следующих событий: <выигрыш выпал на первый билет и не выпал на второй>, <выигрыш не выпал на первый билет и выпал на второй>, <выигрыш выпал на оба билета>, <на оба билета выигрыш не выпал>. Эти события образуют полную группу попарно несовместных событий.
Пример 1.13. Стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: попадание или промах. Эти два несовместных события образуют полную группу.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
3. Операции над событиями: сумма (объединение), произведение (пересечение) и разность событий; диаграммы Вьенна.
Операции над событиями
События обозначаются заглавными буквами начала латинского алфавита A, B, C, D, …, снабжая их при необходимости индексами. Тот факт, что элементарный исход х содержится в событии А, обозначают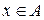 
.
Для понимания удобна геометрическая интерпретация при помощи диаграмм Виенна: представим пространство элементарных событий Ω в виде квадрата, каждой точке которого соответствует элементарное событие. Случайные события А и В, состоящие из совокупности элементарных событий хi и уj, соответственно, геометрически изображаются в виде некоторых фигур, лежащих в квадрате Ω (рис. 1-а, 1-б).
Пусть опыт состоит в том, что внутри квадрата, изображенного на рисунке 1-а, выбирается наугад точка. Обозначим через А событие, состоящее в том, что <выбранная точка лежит внутри левой окружности>(рис.1-а), через В – событие, состоящее в том, что <выбранная точка лежит внутри правой окружности>(рис. 1-б).
Достоверному событию благоприятствует любое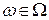 
, поэтому достоверное событие будем обозначать тем же символом Ω.
Два события тождественны друг другу (А=В) тогда и только тогда, когда эти события состоят из одних и тех же элементарных событий (точек).
Суммой (или объединением) двух событий А и В называется событие А+В (или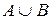 
), происходящее тогда и только тогда, когда происходит или А, или В. Сумме событий А и В соответствует объединение множеств А и В (рис. 1-д).
Пример 1.15. Событие, состоящее в выпадении четного числа, является суммой событий: выпало 2, выпало 4, выпало 6. То есть, <х=четное >= <х=2>+<х=4 >+<х=6 >.
Отметим очевидные соотношения: 
Произведением (или пересечением) двух событий А и В называется событие АВ (или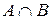 
), происходящее тогда и только тогда, когда происходит и А, и В. Произведению событий А и В соответствует пересечение множеств А и В (рис. 1-е).
Пример 1.16. Событие, состоящее в выпадении 5, является пересечением событий: выпало нечетное число и выпало больше 3-х, то есть, A
Отметим очевидные соотношения: 
Событие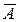 
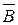
называется противоположным к А, если оно происходит тогда и только тогда, когда А не происходит. Геометрически – это множество точек квадрата, не входящее в подмножество А (рис. 1-в). Аналогично определяется событие 
(рис. 1-г).
Отметим очевидные соотношения: 
Два события называются несовместными, если их одновременное появление в опыте невозможно. Следовательно, если А и В несовместны, то их произведение – невозможное событие: 
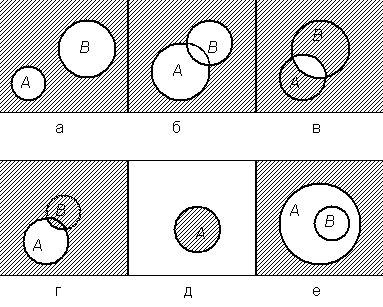
Введенные ранее элементарные события, очевидно, попарно несовместны, то есть 
   |   |
|   |
А В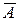 
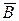
а) б) в) г)
  |    |    |    |
А+В АВ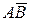 
или А\В В\А или 
Рис. 1. Диаграммы Виенна
Разностью событий А и В называется событие А\В (или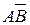 
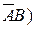
), происходящее тогда и только тогда, когда происходит А, но не происходит В (рис. 1-ж). Аналогично определяется событие В\А (или 
(рис.1-з).
Отметим очевидные соотношения: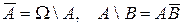 
(рис. 1-г).
Так как разность событий можно выразить с помощью операций отрицания и произведения, пользоваться разностью событий в дальнейшем не будем.
Введенные выше операции сложения и умножения обладают следующими свойствами: А+В=В+А, АВ=ВА, А(В+С)=АВ+АС, А(ВС)=(АВ)С.
Пример 1.18. Производится два выстрела по цели. Пусть событие А –<попадание в цель при первом выстреле>, В ––<попадание при втором выстреле>, тогда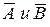 
— промахи, соответственно, при первом и втором выстрелах. Обозначим: событие С – <поражение цели>и примем, что для этого достаточно хотя бы одного попадания. Требуется выразить событие С через события А и В.
Решение. Цель будет поражена в следующих случаях: попадание при первом и промах при втором; промах при первом и попадание при втором; попадание при первом и втором выстрелах. Используя введенные выше операции, перечисленные варианты можно соответственно записать: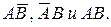 
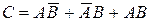
интересующее нас событие заключается в наступлении или первого, или второго, или третьего вариантов (хотя бы одного), то есть
.
С другой стороны, событие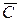 
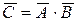
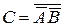
, противоположное событию С, есть промах при двух выстрелах, то есть 
, отсюда искомое событие С можно записать в виде 
. Возможность различного выражения искомого события часто оказывается полезной при решении задач.
4. Относительная частота и вероятность события А. Определение вероятности. Свойства относительной частоты и вероятности. Устойчивость относительной частоты.
Что называют разностью двух событий
тБУУНПФТЙН НОПЦЕУФЧП F УПВЩФЙК, ЛПФПТЩЕ НПЦОП ОБВМАДБФШ Ч ОЕЛПФПТПН УМХЮБКОПН ЬЛУРЕТЙНЕОФЕ. рХУФШ 
– ДПУФПЧЕТОПЕ УПВЩФЙЕ, Б 
– ОЕЧПЪНПЦОПЕ, ФБЛЦЕ РТЙОБДМЕЦБФ НОПЦЕУФЧХ F.
лБЦДПНХ УПВЩФЙА б РПУФБЧЙН Ч УППФЧЕФУФЧЙЕ РТПФЙЧПРПМПЦОПЕ (ДПРПМОЙФЕМШОПЕ) УПВЩФЙЕ, ПВПЪОБЮБЕНПЕ 
Й ПЪОБЮБАЭЕЕ, ЮФП УПВЩФЙЕ ТЕБМЙЪХЕФУС ФПЗДБ Й ФПМШЛП ФПЗДБ, ЛПЗДБ УПВЩФЙЕ б ОЕ ТЕБМЙЪХЕФУС. чЧЕДЕН ЛБЛ БЛУЙПНЩ УМЕДХАЭЙЕ УЧПКУФЧБ ЬФПК ПРЕТБГЙЙ:
; 
; 
.
рТЙНЕТБНЙ РТПФЙЧПРПМПЦОЩИ УПВЩФЙК НПЗХФ УМХЦЙФШ РПРБДБОЙЕ Й РТПНБИ РТЙ ЧЩУФТЕМЕ, ПФЛБЪ РТЙВПТБ Ч ДБООПН ЙОФЕТЧБМЕ ЧТЕНЕОЙ Й ЕЗП ЙУРТБЧОБС ТБВПФБ Ч ФПН ЦЕ ЙОФЕТЧБМЕ ЧТЕНЕОЙ.
дМС ЛБЦДПК РБТЩ УПВЩФЙК б Й ч ЧЧЕДЕН ПРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС.
уПВЩФЙЕ 
ЪБЛМАЮБАЭЕЕУС Ч ФПН, ЮФП ЙЪ ДЧХИ УПВЩФЙК б Й ч РТПЙУИПДЙФ РП ЛТБКОЕК НЕТЕ ПДОП, ОБЪЩЧБАФ ПВЯЕДЙОЕОЙЕН УПВЩФЙК б Й ч.
уПВЩФЙЕ 
(бч), ЪБЛМАЮБАЭЕЕУС Ч ФПН, ЮФП РТПЙУИПДСФ ПДОПЧТЕНЕООП ПВБ УПВЩФЙС б Й ч, ОБЪЩЧБАФ РЕТЕУЕЮЕОЙЕН УПВЩФЙК б Й ч.
пРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС ЛПННХФБФЙЧОЩ Й БУУПГЙБФЙЧОЩ
; 
; 
; 
.
уМЕДХАЭЙЕ ЖПТНХМЩ ЧЧПДСФУС ЛБЛ БЛУЙПНЩ:
чЧЕДЕООЩЕ УППФОПЫЕОЙС РЕТЕОПУСФУС У ДЧХИ УПВЩФЙК ОБ РТПЙЪЧПМШОПЕ ЛПОЕЮОПЕ ОЕРХУФПЕ УЕНЕКУФЧП УПВЩФЙК 
.
пРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС, ОБЛПОЕГ, ДЙУФТЙВХФЙЧОЩ РП ПФОПЫЕОЙА ДТХЗ Л ДТХЗХ:
; 
.
уФТХЛФХТБ, ЛПФПТБС ПВТБЪХЕФУС ОБ НОПЦЕУФЧЕ УПВЩФЙК ЧЧЕДЕООЩНЙ ПРТЕДЕМЕОЙСНЙ Й БЛУЙПНБНЙ, ОБЪЩЧБЕФУС УФТХЛФХТПК ВХМЕЧПК БМЗЕВТЩ. тБУУНПФТЙН ЧУРПНПЗБФЕМШОЩЕ РПОСФЙС, ПРТЕДЕМСЕНЩЕ ОБ ВХМЕЧПК БМЗЕВТЕ УПВЩФЙК.
дЧБ УПВЩФЙС б Й ч, ДМС ЛПФПТЩИ 
ОБЪЩЧБАФУС ОЕРЕТЕУЕЛБАЭЙНЙУС (ЧЪБЙНОП ЙУЛМАЮБАЭЙНЙ). пВЯЕДЙОЕОЙЕ ФБЛЙИ УПВЩФЙК ОБЪЩЧБАФ УХННПК Й ПВПЪОБЮБАФ б + ч ЧНЕУФП 
.
тБЪОПУФША ДЧХИ УПВЩФЙК б Й ч ОБЪЩЧБАФ УПВЩФЙЕ б – ч, УПУФПСЭЙЕ Ч ФПН, ЮФП РТПЙЪПКДЕФ УПВЩФЙЕ б Й ОЕ РТПЙЪПКДЕФ УПВЩФЙЕ ч. пЮЕЧЙДОП, ЮФП 
.
уЙННЕФТЙЮЕУЛПК ТБЪОПУФША ДЧХИ УПВЩФЙК б Й ч ОБЪЩЧБАФ УПВЩФЙЕ 
, ПЪОБЮБАЭЕЕ, ЮФП РТПЙУИПДЙФ МЙЫШ ПДОП ЙЪ б, ч.
уПВЩФЙС 
ПВТБЪХАФ РПМОХА ЗТХРРХ УПВЩФЙК, ЕУМЙ ПОЙ РПРБТОП ОЕ РЕТЕУЕЛБАФУС (ОЕУПЧНЕУФОЩ) Й 
, ФП ЕУФШ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ РТПЙУИПДЙФ ПДОП Й ФПМШЛП ПДОП ЙЪ ОЙИ.
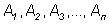
зПЧПТСФ, ЮФП УПВЩФЙЕ б ЧМЕЮЕФ УПВЩФЙЕ ч (ПВПЪОБЮБАФ 
), ЕУМЙ УПВЩФЙЕ ч ПВСЪБФЕМШОП РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ УПВЩФЙС б. еУМЙ УПВЩФЙС б Й ч НПЗХФ РПСЧЙФШУС ЙМЙ ОЕ РПСЧЙФШУС ФПМШЛП ЧНЕУФЕ, ФП ЕУФШ Й 
, ФП ПОЙ ОБЪЩЧБАФУС ЬЛЧЙЧБМЕОФОЩНЙ (б = ч). ьЛЧЙЧБМЕОФОЩЕ УПВЩФЙС ТБЪМЙЮБФШ ОЕ ВХДЕН. пФОПЫЕОЙЕ «ЧМЕЮЕФ» СЧМСЕФУС ПФОПЫЕОЙЕН РПТСДЛБ Ч НОПЦЕУФЧЕ УПВЩФЙК.
вТПУБАЭБСУС Ч ЗМБЪБ БОБМПЗЙС НЕЦДХ УПВЩФЙСНЙ Й НОПЦЕУФЧБНЙ ПВЯСУОСЕФУС ФЕН, ЮФП ЛБЦДПЕ УПВЩФЙЕ УЧСЪБОП У ПРТЕДЕМЕООЩН НОПЦЕУФЧПН ЙУИПДПЧ ЬЛУРЕТЙНЕОФБ ФБЛ, ЮФП ПОП ПВСЪБФЕМШОП РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ ПДОПЗП ЙЪ ЙУИПДПЧ, РТЙОБДМЕЦБЭЙИ ЬФПНХ НОПЦЕУФЧХ, Й ОЕ РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ ПДОПЗП ЙЪ ЙУИПДПЧ, ОЕ РТЙОБДМЕЦБЭЙИ ЬФПНХ НОПЦЕУФЧХ. оБРТЙНЕТ, УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ ВХДЕФ ПДОП РПРБДБОЙЕ, ЕУФШ УХННБ ДЧХИ ОЕРЕТЕУЕЛБАЭЙИУС УПВЩФЙК: РПРБДБОЙЕ 
РТЙ РЕТЧПН Й РТПНБИ 
РТЙ ЧФПТПН ЧЩУФТЕМЕ Й РТПНБИ РТЙ РЕТЧПН 
Й РПРБДБОЙЕ 
РТЙ ЧФПТПН ЧЩУФТЕМЕ
.
дМС УФТПЗПЗП НБФЕНБФЙЮЕУЛПЗП ПВПУОПЧБОЙС, ЧЧПДСФ РПОСФЙЕ ЬМЕНЕОФБТОПЗП УПВЩФЙС.
ьМЕНЕОФБТОЩН УПВЩФЙЕН ОБЪЩЧБЕФУС УПВЩФЙЕ, ОЕ УПДЕТЦБЭЕЕ ОЙЛБЛЙИ РПДУПВЩФЙК, ЛТПНЕ ОЕЧПЪНПЦОПЗП УПВЩФЙС Й УБНПЗП УЕВС
ч ТБНЛБИ ЬЛУРЕТЙНЕОФБ, ЬМЕНЕОФБТОПЕ УПВЩФЙЕ ЬФП ТЕЪХМШФБФ ЬЛУРЕТЙНЕОФБ. лБЦДПЕ, ПФОПУСЭЕЕУС Л ТБУУНБФТЙЧБЕНПК НПДЕМЙ ЬМЕНЕОФБТОПЕ УПВЩФЙЕ, ЧМЕЮЕФ МЙВП ОБУФХРМЕОЙЕ, МЙВП ОЕ ОБУФХРМЕОЙЕ ЛБЦДПЗП ДБООПЗП УПВЩФЙС, УЧСЪБООПЗП У ТБУУНБФТЙЧБЕНПК НПДЕМША. оБРТЙНЕТ, РТЙ ПДОПН ЧЩУФТЕМЕ РП НЙЫЕОЙ ЬМЕНЕОФБТОЩН УПВЩФЙЕН ВХДХФ РТПНБИ Й РПРБДБОЙЕ. ч ЬЛУРЕТЙНЕОФЕ – РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ ВХДЕФ ПДОП РПРБДБОЙЕ – ЬМЕНЕОФБТОЩНЙ УПВЩФЙСНЙ ВХДХФ: РПРБДБОЙЕ РТЙ РЕТЧПН Й РТПНБИ РТЙ ЧФПТПН ЧЩУФТЕМЕ Й РТПНБИ РТЙ РЕТЧПН Й РПРБДБОЙЕ РТЙ ЧФПТПН ЧЩУФТЕМЕ.
уМХЮБКОЩК ЬЛУРЕТЙНЕОФ ОБЪЩЧБЕФУС ЛПОЕЮОЩН, ЕУМЙ ЙНЕЕФУС РПМОБС ЗТХРРБ ЬМЕНЕОФБТОЩИ УПВЩФЙК.
ч ФЕПТЙЙ ЧЕТПСФОПУФЕК ТБУУНБФТЙЧБАФУС МЙЫШ ФБЛЙЕ УМХЮБКОЩЕ ЬЛУРЕТЙНЕОФЩ, Ч ЛПФПТЩИ ЛБЦДПЕ УПВЩФЙЕ СЧМСЕФУС УХННПК ЧУЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК, ЧМЕЛХЭЙИ ЬФП УПВЩФЙЕ. фБЛПК УМХЮБКОЩК ЬЛУРЕТЙНЕОФ ПРЙУЩЧБЕФУС НОПЦЕУФЧПН ЬМЕНЕОФБТОЩН УПВЩФЙК, УЧСЪБООЩИ У ОЙН Й ОЕЛПФПТЩН ЛМБУУПН ЕЗП РПДНОПЦЕУФЧ, ОБЪЩЧБЕНЩИ УПВЩФЙСНЙ Й ОБЪЩЧБЕФУС РТПУФТБОУФЧПН ЬМЕНЕОФБТОЩИ УПВЩФЙК. пВПЪОБЮБЕФУС ПВЩЮОП 
. рТЙ ЬФПН МАВПЕ ЬМЕНЕОФБТОПЕ УПВЩФЙЕ – ФПЮЛБ РТПУФТБОУФЧБ ПВПЪОБЮБЕФУС ВХЛЧПК 
.
дПУФПЧЕТОПЕ УПВЩФЙЕ РТЕДУФБЧМСЕФ УПВПК НОПЦЕУФЧП ЧУЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК . оЕЧПЪНПЦОПЕ УПВЩФЙЕ РТЕДУФБЧМСЕФ УПВПК РХУФПЕ НОПЦЕУФЧП 
.
оБРТЙНЕТ, РТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК Ч ЬЛУРЕТЙНЕОФЕ, ЪБЛМАЮБАЭЕНУС Ч ФПН, ЮФП ОБВМАДБЕФУС РПРБДБОЙЕ ЙМЙ РТПНБИ РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ УПУФПЙФ ЙЪ ЮЕФЩТЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК: ДЧБ РПРБДБОЙС, РПРБДБОЙЕ – РТПНБИ, РТПНБИ – РПРБДБОЙЕ, ДЧБ РТПНБИБ.
дМС ОБЗМСДОПУФЙ РПУФТПЕООПК НБФЕНБФЙЮЕУЛПК НПДЕМЙ УМХЮБКОЩИ СЧМЕОЙК ХДПВОП ХУМПЧОП УЮЙФБФШ РТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК ОЕЛПФПТПК ПВМБУФША РМПУЛПУФЙ (ЛЧБДТБФПН), ЬМЕНЕОФБТОПЕ УПВЩФЙЕ — ФПЮЛБНЙ ЬФПК ПВМБУФЙ; РТЙ ЬФПН УПВЩФЙС ХДПВОП ЙЪПВТБЦБФШ Ч ЧЙДЕ ОЕЛПФПТЩИ ЖЙЗХТ (ЛТХЗПЧ).
оБ ТЙУХОЛБИ РТЕДУФБЧМЕОЩ ЙЪПВТБЦЕОЙС УМЕДХАЭЙИ ПРЕТБГЙК:
Б). б Й ч – ОЕУПЧНЕУФОЩЕ УПВЩФЙС;
В).— ПВЯЕДЙОЕОЙЕ УПВЩФЙК б Й ч;
Ч). бч – РЕТЕУЕЮЕОЙЕ УПВЩФЙК б Й ч;
З). б – ч – ТБЪОПУФШ УПВЩФЙК б Й ч;
Д). — РТПФЙЧПРПМПЦОПЕ Л б УПВЩФЙЕ;
Е). — УПВЩФЙЕ ч ЧМЕЮЕФ УПВЩФЙЕ б.
чБЦОЩН РТЙНЕТПН УМХЮБКОПЗП ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ЬЛУРЕТЙНЕОФ, Ч ЛПФПТПН ЙЪНЕТСЕФУС ОЕЛПФПТБС ЧЕМЙЮЙОБ и. ч ЛБЮЕУФЧЕ ЬМЕНЕОФБТОЩИ УПВЩФЙК ЪДЕУШ НПЦОП ЧЪСФШ УПВЩФЙС ЧЙДБ (и = И), ЗДЕ И – ОЕЛПФПТПЕ ЖЙЛУЙТПЧБООПЕ ЪОБЮЕОЙЕ. нОПЦЕУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК ЕУФЕУФЧЕООП ПФПЦДЕУФЧЙФШ У НОПЦЕУФЧПН ФПЮЕЛ ОБ РТСНПК. еУМЙ БРТЙПТЙ ЙЪЧЕУФОП, ЮФП и НПЦЕФ РТЙОЙНБФШ МЙЫШ ЪОБЮЕОЙС ЙЪ ОЕЛПФПТПЗП НОПЦЕУФЧБ н, ФП ЬФП НОПЦЕУФЧП Й УМЕДХЕФ ТБУУНБФТЙЧБФШ ЛБЛ НОПЦЕУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК. ч РТПГЕУУЕ ЙЪНЕТЕОЙС ЕУФЕУФЧЕООП РТЕДРПМБЗБФШ ЧПЪНПЦОПУФШ ОБВМАДЕОЙС УПВЩФЙС 
, ЗДЕ Б Й b – РТПЙЪЧПМШОЩЕ ЮЙУМБ. чУЕЧПЪНПЦОЩЕ ЛПОЕЮОЩЕ УХННЩ ФБЛЙИ РПМХЙОФЕТЧБМПЧ НПЦОП ТБУУНБФТЙЧБФШ ЛБЛ БМЗЕВТХ УПВЩФЙК, УЧСЪБООЩИ У ЬЛУРЕТЙНЕОФПН.