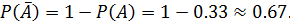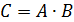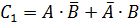Что называют произведением нескольких событий
Теория вероятности. Часть 2
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.
Подборку задач на отработку темы смотрите здесь.
Что называют произведением нескольких событий
Теория вероятности
Навигация
Лекция 2: Основные понятия теории вероятностей. Теоремы сложения и умножения
1. Предмет теории вероятностей.
2. Краткая историческая справка.
3. Виды случайных событий.
4. Определение вероятности.
5. Теорема сложения вероятностей.
6. Теорема умножения вероятностей.
1. Предмет теории вероятностей.
Наблюдаемые нами явления (события) можно разделить на 3 вида: достоверные, невозможные и случайные.
Пример: Событие А- «Вода находится в сосуде в жидком состоянии» является достоверным, если она содержится при нормальном атмосферном давлении и температуре 20 градусов по Цельсию.
Пример: Событие А- «Вода находится в сосуде в твердом состоянии» является достоверным, если она содержится при нормальном атмосферном давлении и температуре 20 градусов по Цельсию.
Пример: Брошена монета. Событие А- «При бросании на монете выпал герб» является случайным.
Каждое случайное событие есть следствие действий многих случайных причин (сила, с которой брошена монета, форма монеты и т.д.). Учесть влияние всех этих причин невозможно, поскольку число их очень велико и законы их действия неизвестны. Поэтому, теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет. Она просто не в силах этого сделать.
Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, можно предсказать с небольшой погрешностью число появления герба при подбрасывании монеты большого числа раз.
2. Краткая историческая справка.
Задача кавалера де Мере: Два игрока поставили поровну, начали игру и условились, что тот кто раньше выиграет известное число партий, получит всю ставку. По некоторым обстоятельствам игра не могла быть окончена и прекратилась в тот момент, когда первому игроку не хватало до конца одной, а второму- двух побед. Спрашивается: «Как игроки должны поделить ставку между собой?». (Ответ: 3:1)
Эту задачу в 1654 году кавалер де Мере предложил для решения своему другу, знаменитому Блезу Паскалю. Тот решил ее и для более общего случая. Решив задачу сам, Паскаль предложил решить ее своему не менее знаменитому современнику Пьеру Ферма. Каждый из них решил задачу своим способом, и на основе этого у них завязалась переписка.
Таким образом, были положены основы математической теории вероятностей.
Страстный игрок в кости кавалер де Мере так же относится к числу основателей теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял известных математиков решать различные задачи, на которые наталкивался сам.
Следующий этап развития теории вероятностей связан с именами Якова Бернулли (доказанная им теорема, получившая название «Закон больших чисел», была первым теоретическим обоснованием накопленных ранее фактов.), Карла Гаусса, Пьера-Симона Лапласса, Абрахама де Муавра и т.д.
Случайные события или просто события принято обозначать заглавными буквами латинского алфавита А, В, С и т.д.
В дальнейшем, «совокупность условий» будем заменять на краткое выражение «произошло испытание».
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Полной группой случайных событий называется группа всевозможных, равновозможных и единственно-возможных событий.
События называются равновозможными, если есть основание считать, что ни одно из них не является более возможным, чем другое.
4. Определение вероятности.
4.1 Классическое определение вероятности (определяет количественные шансы наступления случайного события)
Вероятностью случайного события А называется отношение числа благоприятных случаев к общему числу всевозможных, равновозможных и единственно-возможных случаев.
Свойство 1: Вероятность достоверного события равна 1.
Свойство 2: Вероятность невозможного события равна 0.
Доказательство: т.к. m =0, то:
Свойство 3: Вероятность случайного события есть положительно число, заключенное между 0 и 1.
1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найдите вероятность того, что набрана нужная цифра.
2. В партии из 10 изделий- 7 нестандартных. Найдите вероятность того, что среди 6-ти взятых наудачу изделий:
а) все шесть нестандартные;
3. На карточках написаны буквы И, В, А, Н, О, В. Карточки перемешивают и раскладывают в ряд. Найдите вероятность того, что при этом получится фамилия «Иванов»?
Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо.
4.2 Статистическое определение вероятности (экспериментальное, опытное определение).
Статистической вероятностью события А называется отношение числа благоприятствующих исходов опытов к общему числу проведенных опытов (испытаний).
4.3 Геометрическое определение вероятности (вероятность попадания точки в заданную область).
Пример: На территории крытой военной базы стоит 4 цистерны. Какова вероятность прямого попадания с воздуха в одну из цистерн?
5. Теорема сложения вероятностей.
Суммой случайных событий А и В называется событие А+В, состоящее как из исходов, благоприятствующих событию А, так и из исходов, благоприятствующих событию В. (Исходы, благоприятствующие событиям А и В одновременно, считаются только один раз.)
Понятие суммы распространяется на любое число случайных событий А, В, С и т.д.
Пример: Из орудия произведено 2 выстрела. Событие А- «Зафиксировано попадание при первом выстреле», Событие В- «Зафиксировано попадание при втором выстреле», Событие А+В – «Зафиксировано попадание хотя бы при одном из двух выстрелов».
Теорема: Если случайные события А и В несовместны, то Р(А+В)=Р(А)+Р(В).
Пример: В урне имеется 30 шаров: 10- красных, 5- синих, 15- белых. Найдите вероятность появления цветного (не белого) шара.
Решение: Пусть событие А-«Случайным образом вынули красный шар», событие В- «Случайным образом вынули синий шар, событие А+В- «Случайным образом вынули красный или синий (цветной) шар». Т. К. события А и В- несовместны, то:
Случайные события А и называются противоположными, если они несовместны и в сумме образуют достоверное событие.
Пример: Вероятность того, что день будет дождливым равна 0,7. Найдите вероятность того, что день будет не дождливым.
Решение: p =0,7, q =1- p =1-0,7=0,3.
Пример: В XVII веке во Франции страстный игрок в кости рыцарь де Мере хотел разбогатеть при помощи игры в кости и для этого он придумывал различные усложненные правила игры. Однажды, де Мере придумал следующие правила:
Первая игра де Мере: Игральная кость подбрасывается 4 раза. Рыцарь бился об заклад, что при этом хотя бы один раз выпадет 6 очков.
Рыцарь стал часто выигрывать и с ним перестали играть. Тогда он придумал вторую игру.
Вторая игра де Мере: 2 игральные кости подбрасывают 24 раза. Рыцарь бился об заклад, что при этом хотя бы один раз выпадут две шестерки.
Эта игра его разорила.
Теорема: Если случайные события не совместны в совокупности, то
Следствие: Если случайные события образуют полную группу несовместных событий, то сумма их вероятностей равна…
. События образуют полную группу случайных событий.
Произведением случайных событий А и В называют событие A*B, состоящее из тех и только тех исходов, которые благоприятствуют одновременно и событию А, и событию В.
Пример: Бросают 2 игральные кости и рассматривают случайные события А- «На первой кости выпало четное число очков (2 k )» и В- «На второй кости выпало число очков, кратное трем (3 l )». всех возможным исходов при этом- 36 (6 * 6). Событию А благоприятствует 18 исходов. Событию В благоприятствует 12 исходов. Событию A*B благоприятствует 6 исходов. (2-3; 4-3; 6-3; 2-6; 4-6; 6-6).
Теорема: Для любых случайных событий А и В справедливо равенство:
Доказательство: т.к. число A*B при суммировании исходов, благоприятствующих каждому из событий считается дважды, то один раз это число необходимо отнять.
Пример: Найдите вероятность того, что при бросании игральной кости выпадет грань с четным числом очков или числом очков кратным трем.
Решение: Событие А-« На кости выпало четное число очков», событие В- «На кости выпало число очков кратное трем». События А и В- совместны.
6. Теорема умножения вероятностей.
Случайное событие А называется независимым от события В, если вероятность наступления события А не зависит от того, произошло событие В или нет.
Пример: Подбросили 2 монеты. Появление герба на второй монете не зависит от того, что выпало на первой и наоборот. Это два независимых друг от друга события.
Вероятность случайного события А, вычисленная при условии, что событие В имело место, называется условной вероятностью и обозначается Р(А/В).
Если А и В- независимые случайные события, то Р(А/В)=Р(А) и Р(В/А)=Р(В).
Теорема: Вероятность произведения двух случайных событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
В урне 15 белых шаров и 20- черных. Найдите вероятность того, что оба шара, вынутых наудачу- белые.
Решение: Событие А- «Первым вынули белый шар», событие В- «вторым вынули белый шар». Тогда,
Теорема: Вероятность произведения нескольких случайных событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место.
Теорема: Вероятность произведения двух независимых случайных событий равна произведению вероятностей этих событий. P(A*B)=P(A)*P(B)
Доказательство: P(A*B)=P(A)*P(B/A)= P(A)*P(B), т.к. А и В- независимы. Ч.т.д.
Пример: В урне 7 белых шаров и 6- черных. Вынули первый шар, запомнили его цвет и вернули его обратно. После этого вынули второй шар. Найдите вероятность, что оба шара были белые.
Решение: Событие А- «Первым вынули белый шар», событие В- «Вторым вынули белый шар». События А и В – независимы. Тогда
Теорема: Вероятность произведения нескольких независимых случайных событий равна произведению их вероятностей.
Пример: Производится 3 выстрела по мишени. Вероятность попадания при первом выстреле равна 0,7, при втором- 0,8, при третьем- 0,9. Найдите вероятность того, что в результате этих трех выстрелов будет ровно одна пробоина.
Событие А- «будет одна пробоина в результате трех выстрелов».
Р(А)=0, 7*0,2 * 0,1+0,3 * 0,8 *0,1+0,3 * 0,2 * 0,9=0,014+0,024+0,054=0,092
Рассмотрим решение задачи кавалера де Мере.
Событие А- «Победил первый игрок».
Первый игрок может победить в первой же игре или во второй (потерпев в первой игре поражение). Тогда
Т.е. вероятность, что первый игрок одержит победу, равна 3/4. Для второго игрока эта вероятнсоть равна 1/3. Ставку необходимо разделить 3:1.
1. По преданию, когда-то в сельской местности России среди девушек существовало гадание. Одна из подруг зажимала в руке 6 травинок так, чтобы концы травинок торчали сверху и снизу, а другая девушка связывала эти травинки попарно между собой сверху и снизу. Если при этом все шесть травинок оказывались связанными в одно кольцо, то это должно было означать, что девушка в текущем году выйдет замуж. Какова вероятность этого события?
Гадание чаще всего сбывалось, т.к. в этом возрасте действительно примерно 50 % девушек выходило замуж.
2. В XVII веке в Генуе возникла знаменитая лотерея. Генуэзская лотерея в XVIII веке разыгрывалась во Франции, Германии и других европейских странах. В лотерее разыгрывается 90 номеров, из которых выигрывают 5. По условию можно ставить ту или иную ставку на любой из 90 номеров или на любую совокупность 2-ух, 3-ех,4-ех или 5-ти номеров. Если участник лотереи ставит на один номер, то он получает при выигрыше в 15 раз больше ставки, если на 2 номера (амбо), то в 270 раз, если на 3 (терн)- в 5500 раз, если на 4 (катерн)- в 75000 раз, елс на 5 (квин)- в 1000000 раз. Какова вероятность выиграть в каждом из указанных 5-ти случаев.
Понятия суммы и произведения событий



Сумма всех вероятностей событий выборочного пространства равняется 1. Например, если экспериментом является подбрасывание монеты при Событии А = «орел» и Событии В = «решка», то А и В представляют собой все выборочное пространство. Значит, Р(А) +Р(В) = 0.5 + 0.5 = 1.
Пример. В ранее предложенном примере вычисления вероятности извлечения из кармана халата красной ручки (это событие А), в котором лежат две синих и одна красная ручка, Р(А) = 1/3 ≈ 0.33, вероятность противоположного события – извлечения синей ручки – составит
Прежде чем перейти к основным теоремам, введем еще два более сложных понятия — сумма и произведение событий. Эти понятия отличны от привычных понятий суммы и произведения в арифметике. Сложение и умножение в теории вероятностей — символические операции, подчиненные определенным правилам и облегчающие логическое построение научных выводов.
Суммой нескольких событий является событие, заключающееся в появлении хотя бы одного из них. То есть, суммой двух событий А и В называется событие С, состоящее в появлении или события А, или события В, или событий А и В вместе.
Например, если пассажир ждет на остановке трамваев какой-либо из двух маршрутов, то нужное ему событие заключается в появлении трамвая первого маршрута (событие А), или трамвая второго маршрута (событие В), или в совместном появлении трамваев первого и второго маршрутов (событие С). На языке теории вероятностей это значит, что нужное пассажиру событие D заключается в появлении или события А, или события В, или события С, что символически запишется в виде:
Произведением двух событийА и В является событие, заключающееся в совместном появлении событий А и В. Произведением нескольких событий называется совместное появление всех этих событий.
В приведенном примере с пассажиром событие С (совместное появление трамваев двух маршрутов) представляет собой произведение двух событий А и В, что символически записывается следующим образом:
Допустим, что два врача порознь осматривают пациента с целью выявления конкретного заболевания. В процессе осмотров возможно появление следующих событий:
— обнаружение заболеваний первым врачом (А);
— необнаружение заболевания первым врачом ( 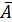
— обнаружение заболевания вторым врачом (В);
— необнаружение заболевания вторым врачом ( 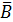
Рассмотрим событие, которое заключается в том, что заболевание будет обнаружено в процессе осмотров ровно один раз. Это событие может реализоваться двумя способами:
— заболевание обнаружит первый врач (А) и не обнаружит второй ( 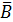
— заболеваний не обнаружит первый врач ( 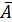
Обозначим рассматриваемое событие через 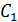
Рассмотрим событие, которое заключается в том, что заболевание будет обнаружено в процессе осмотров дважды (и первым, и вторым врачом). Обозначим это событие через 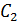
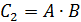
Событие, заключающееся в том, что ни первый, ни второй врач заболевания не обнаружит, обозначим через 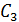
1.2.3. Сложение и умножение событий
Пожалуйста, запомните ВАЖНЕЙШЕЕ ПРАВИЛО, без которого освоить тервер просто нереально:
Сложение событий обозначает логическую связку ИЛИ,
а умножения событий – логическую связку И.
1) Суммой двух событий 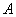
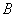
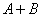
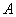
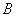
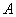
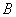
Правило распространяется и на бОльшее количество слагаемых, например, событие 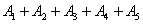
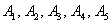
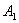
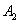
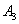
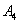
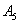
Событие 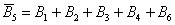
Все примеры ОСМЫСЛЕННО проговариваем ВСЛУХ!
Это важно.
Событие 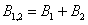
Событие 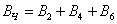
Событие 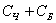
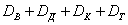
Чуть занятнее дело с событиями совместными:
Событие 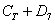
Событие 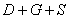
– будет только дождь / только гроза / только солнце;
– или наступит только какая-нибудь пара событий (дождь + гроза / дождь + солнце / гроза + солнце);
– или все три события появятся одновременно.
То есть, событие 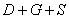
Второй столп алгебры событий:
2) Произведением двух событий 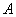
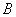
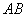
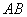
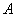
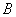
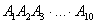
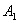
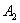
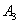
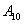
Рассмотрим испытание, в котором подбрасываются две монеты (не имеет значения, одновременно или нет) и следующие события:
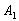
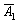
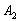
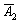
Тогда:
– событие 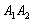
– событие 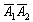
– событие 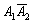
– событие 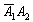
Осмысливаем и проговариваем вслух!!
Очевидно, что события 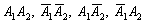
Давайте просуммируем данные события: 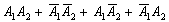
Это был пример, когда в одном испытании задействовано несколько объектов, в данном случае две монеты. Другая распространенная в практических задачах схема – это повторные испытания, когда, например, один и тот же игральный кубик бросается 3 раза подряд. В качестве демонстрации рассмотрим следующие события:
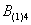
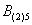
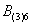
Тогда событие 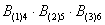
…понимаю, что разбираются не очень интересные примеры, но это часто встречающиеся в задачах вещи и от них никуда не деться. Помимо монетки, кубика и колоды карт вас поджидают урны с разноцветными шарами, несколько стрелков, стреляющих по мишени, и неутомимый рабочий, который постоянно вытачивает какие-то детали =)
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин