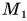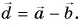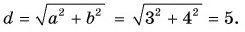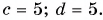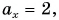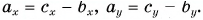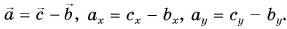Что называют проекцией вектора на координатную ось сделайте пояснительный рисунок
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Как определяют проекцию вектора на ось
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 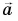
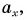
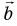
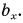
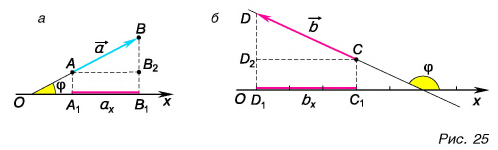
Проекция 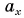
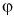
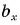
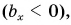
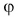
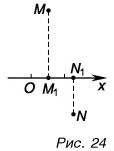
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 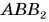
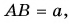
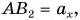
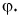
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
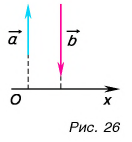
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 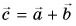
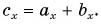
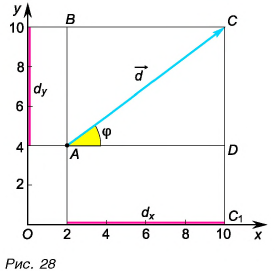
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
Рассмотрим вектор 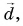
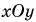
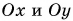
Модуль вектора 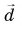
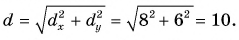
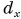
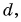
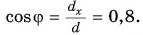
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
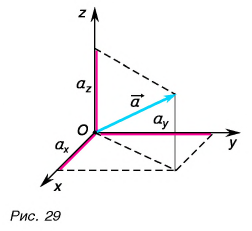
Вектор в пространстве определяется тремя проекциями: 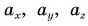
Главные выводы:
Пример №1
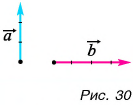
1. Определите сумму и разность взаимно перпендикулярных векторов 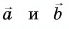
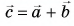
Решение
Сумму векторов 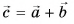
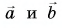
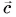
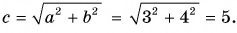
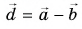
Модуль вектора 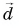
Ответ:
Пример №2
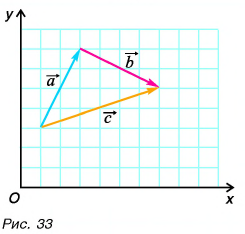
Выразите вектор 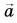
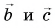
Решение
По правилу треугольника находим: 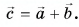
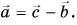
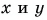
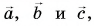
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
§ 5. ПРОЕКЦИИ ВЕКТОРА НА КООРДИНАТНЫЕ ОСИ. ДЕЙСТВИЯ НАД ПРОЕКЦИЯМИ. Вопросы
1. Что называют проекцией вектора на координатную ось?
1. Проекцией вектора а на координатную ось называют длину отрезка между проекциями начала и конца вектора а (перпендикулярами, опущенными из этих точек на ось) на эту координатную ось.
2. Как связан вектор перемещения тела с его координатами?
2. Проекции вектора перемещения s на оси координат равны изменению соответствующих координат тела.
3. Если координата точки с течением времени увеличивается, то какой знак имеет проекция вектора перемещения на координатную ось? А если она уменьшается?
3. Если координата точки с течением времени увеличивается, то проекция вектора перемещения на координатную ось будет положительной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора по направлению самой оси.
Если координата точки с течением времени будет уменьшаться, то проекция вектора перемещения на координатную ось будет отрицательной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора против направляющей самой оси.
4. Если вектор перемещения параллелен оси X, то чему равен модуль проекции вектора на эту ось? А модуль проекции этого же вектора на ось У?
4. Если вектор перемещения параллелен оси Х, то модуль проекции вектора на эту ось равен модулю самого вектора, а его проекция на ось Y равна нулю.
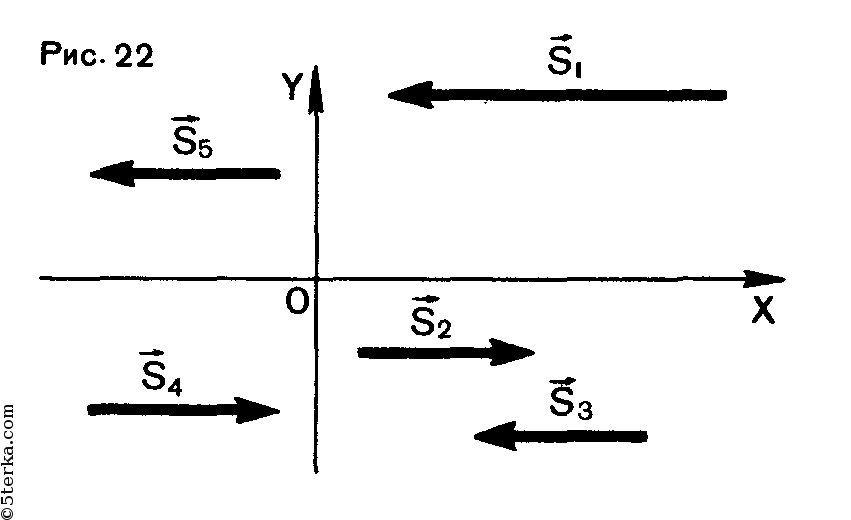
5. Определите знаки проекций на ось X векторов перемещения, изображенных на рисунке 22. Как при этих перемещениях изменяются координаты тела?
5. Во всех нижеследующих случаях координата Y тела не изменяется, а координата Х тела будет изменяться следующим образом:
6. Если значение пройденного пути велико, то может ли модуль перемещения быть малым?
6. Может. Это связано с тем, что перемещение (вектор перемещения) является векторной величиной, т.е. представляет собой направленный отрезок прямой, соединяющий начальное положение тела с его последующими положениями. А конечное положение тела (вне зависимости от величины пройденного пути) может находиться как угодно близко к первоначальному положению тела. В случае совпадения конечного и начального положений тела, модуль перемещения будет равен нулю.
7. Почему в механике более важен вектор перемещения тела, чем пройденный им путь?
7. Основной задачей механики является определение положения тела в любой момент времени. Зная вектор перемещения тела мы можем определить координаты тела, т.е. положение тела в любой момент времени, а зная только пройденный путь мы не можем определить координаты тела, т.к. мы не имеем сведений о направлении движения, а можем только судить о длине пройденного пути на данный момент времени.
Что называют проекцией вектора на координатную ось сделайте пояснительный рисунок
1. Какая величина называется векторной (или просто вектором)?
Физическая величина, которая характеризуется не только числовым значением (модулем), но и направлением, называется векторной величиной (или просто вектором).
Для векторной величины одинаково важны числовое значение (модуль) и направление.
Примеры векторных величин:
— скорость,
— перемещение,
— сила.
2. Какая величина называются скалярной (или просто скаляром)?
Величины, которые не имеют направления и задаются только числом, называются скалярными величинами или скалярами.
Примеры скалярных величин:
3. Как изображают векторную величину?
Векторную величину изображают в виде стрелки, которая начинается в некоторой точке и заканчивается острием, указывающим направление..
Такой отрезок-стрелка называется вектором.
Длина стрелки в выбранном масштабе выражает модуль векторной величины.
Векторы обозначают буквами со стрелкой над ними.
Такой же буквой, но без стрелки обозначают модуль вектора.
4. Если два вектора равны друг другу по модулю, но направления векторов различны, то можно ли сказать, что эти векторы равны друг другу?
Нет, нельзя.
Равными считаются векторы, у которых одинаковы и модули, и направления.
5. Чем отличается векториая величина от скалярной?
Проекция вектора на координатную ось
1. Как построить проекцию вектора на координатную ось?

Есть вектор а.
Опустим из точки А (начало вектора) и точки В (конец вектора) перпендикуляры на ось ОX.
Получим на оси точки ха и хв — это проекции точек А и В на ось ОX.
Длину отрезка ха-хв между проекциями начала и конца вектора называют проекцией вектора а на ось ОX и обозначают, как ах.
Проекцию вектора на ось обозначают той же буквой, что и вектор, но без стрелки и с индексом оси.
Проекция вектора — величина скалярная.
2. Если вектор перемещения параллелен координатной оси, то чему равен модуль проекции вектора на эту ось?
Если вектор параллелен оси координат, то модуль его проекции ( |ax| ) равен модулю ( a ) самого вектора.
3. Что называют проекцией вектора на координатную ось?
Длину отрезка на координатной оси между проекциями начала и конца вектора, взятую со знаком « + » или « —», называют проекцией вектора а на координатную ось.
Проекция вектора на координатную ось может быть, как положительной, так и отрицательной.
Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью.
Проекция вектора на ось считается отрицательной, если вектор направлен противоположно оси.
Если вектор перпендикулярен координатной оси, то при любом направлении вектора его проекция на ось равна нулю.
Проекция вектора на ось. Проекция вектора на вектор
 |
| рис. 1 |
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
| b | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
Найдем проекцию вектора a на вектор b
| Пр b a = | a · b | = | 11 | = 2.2 |
| | b | | 5 |
Примеры вычисления проекции вектора для пространственных задачи
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
| b | = √ 4 2 + 2 2 + 4 2 = √ 16 + 4 + 16 = √ 36 = 6
Найдем проекцию вектора a на вектор b
| Пр b a = | a · b | = | 12 | = 2 |
| | b | | 6 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Проекция вектора на ось. Скалярное произведение векторов
По этой ссылке вы найдёте полный курс лекций по математике:
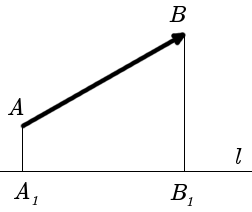
Опуская из его начала и конца перпендикуляры на заданную ось I, построим на ней направленный отрезок CD (рис. 24). Определение. Проекцией вектора АВ на ось I называется величина направленного отрезка CD, построенного указанным выше способом. Основные свойства проекций 1. Проекция вектора АВ на какую-либо ось I равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25) 2.
Заметив, что (b| cosy> есть проекция вектора b на направление вектора а, можем написать (рис. 27 6) и,аналогично, (рис.27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или Ь — нулевой, будем считать, что Проекция вектора на ось.
Скалярное произведение векторов 5.1.
Свойства скалярного произведения 1. Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и Ь ортогональны, a J.h. Это следует из формулы (1), определяющей скалярное произведение. Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так: 2.
Возможно вам будут полезны данные страницы:
Скалярное произведение векторов, заданных координатами Пусть векторы а и Ь заданы своими координатами в ортонор миро ванном базисе Рассмотрим скалярное произведение векторов и и Ь: Проекция вектора на ось. Скалярное произведение векторов Пользуясь распределительным свойством скалярного произведения, находим Учитывая, что Тоесть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат. Пример.
| Найти скалярное произведение векторов |
Тогда формула (7) примет следующий вид cos Пример. Найти угол между векторами Пользуясь формулой (8), находом Пусть b = i, т.е. b = <1,0, 0>. Тогда для всякого вектора О имеем Проекция вектора на ось. Скалярное произведение векторов или, в координатной записи, где q есть угол, образованный вектором а с осью Ох.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.