Что называют пределом функции

10.04.202214.04.2022 admin 0 Comments

Предел функции: основные понятия и определения

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

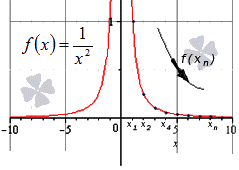
При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

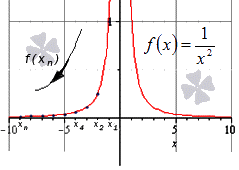
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

Решение

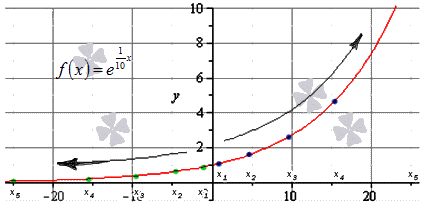
Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Решение

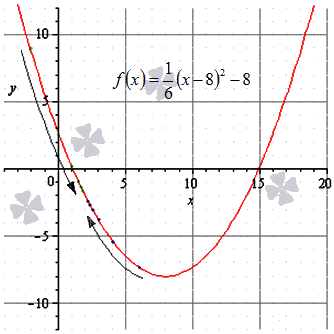
Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник

Предел функции.

Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Или другими словами, число A является пределом функции y = f (x) в точке x₀, если для всякой последовательности точек из области определения функции, не равных x₀, и которая сходится к точке x₀ (lim x_n = x0), последовательность соответствующих значений функции сходится к числу A.

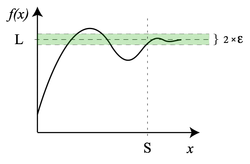
График функции, предел которой при аргументе, который стремится к бесконечности, равен L:

Предел функции по Гейне.

Значение А является пределом (предельным значением) функции f (x) в точке x₀ в случае, если для всякой последовательности точек , которая сходится к x₀, но которая не содержит x₀ как один из своих элементов (т.е. в проколотой окрестности x₀), последовательность значений функции сходится к A.

Предел функции по Коши.

Ответ

Необходимо рассчитать предел

Таким образом, числитель будет таким:

Далее сокращаем числитель и знаменатель на (x – 1):

Ответ

Решение пределов функции.

Чтобы решить пределы, следуйте правилам:

Разобравшись в сути и основных правилах решения предела, вы получите базовое понятие о том, как их решать.

Источник

Предел функции

Из Википедии — свободной энциклопедии

Преде́лом фу́нкции (предельным значением функции) в точке, предельной для области определения функции, называется такая величина, к которой значение рассматриваемой функции стремится при стремлении её аргумента к данной точке. Одно из основных понятий математического анализа.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в любой окрестности данной точки существуют точки области определения. Это позволяет говорить о стремлении аргумента функции к данной точке. При этом предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо конкретно указывать способ сходимости функции, для чего вводят так называемую базу подмножеств области определения функции, и тогда определение предела функции формулируют по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Также благодаря рассмотрению расширенной вещественной прямой (на которой базу окрестностей можно построить и для бесконечно удалённой точки) можно определить такие понятия, как предел функции при стремлении аргумента к бесконечности, а также стремление самой функции к бесконечности. Предел последовательности (как предел функции натурального аргумента) как раз представляет собой пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции в точке означает, что для любого заданного значения области значений можно подобрать такую окрестность этого значения, что в любой сколь угодно малой окрестности точки, в которой функция принимает заданное значение, существуют точки, значение функции в которых окажется за пределами указанной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной в данной точке.

Источник

Предел функции

x
1	0.841471
0.1	0.998334
0.01	0.999983

Хотя функция (sin x)/x в нуле не определена, когда x приближается к нулю, значение (sin x)/x становится сколь угодно близко к 1.

Другими словами, предел функции (sin x)/x при x, стремящемся к нулю, равен 1.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция оказывается непрерывной (в данной точке).

Предел фу́нкции — одно из основных понятий математического анализа.

Содержание

Определения

Рассмотрим функцию , определённую на некотором множестве , которое имеет предельную точку (которая, в свою очередь, не обязана ему принадлежать).

Предел функции по Гейне

Значение называется пределом (предельным значением) функции в точке , если для любой последовательности точек , сходящейся к , но не содержащей в качестве одного из своих элементов (то есть в проколотой окрестности ), последовательность значений функции сходится к . [1]

Предел функции по Коши

Значение называется пределом (предельным значением) функции в точке , если для любого наперёд взятого положительного числа найдётся отвечающее ему положительное число такое, что для всех аргументов , удовлетворяющих условию , выполняется неравенство . [1]

\exists \delta = \delta \left( \varepsilon \right)

Окрестностное определение по Коши

Значение называется пределом (предельным значением) функции в точке , если для любой окрестности точки существует выколотая окрестность точки такая, что образ этой окрестности лежит в . Фундаментальное обоснование данного определения предела можно найти в статье Предел вдоль фильтра.

Предел по базе множеств

Наиболее общим определением является определение предела функции по базе (по базису фильтра, по фильтру).

Пусть — некоторая база подмножеств области определения. Тогда

Если — предельная точка множества , то это означает, что каждая проколотая окрестность точки в множестве не пуста, а, значит, существует база проколотых окрестностей в точке . Эта база имеет специальное обозначение «» и читается «при , стремящемся к по множеству ». Если область определения функции совпадает с , то значок множества опускается, тогда база обозначается совсем просто «» и читается «при , стремящемся к ».

При рассмотрении только числовых функций вещественного переменного также рассматриваются и базы односторонних окрестностей. Для этого рассматриваются два множества:

Соответственно этому вводятся две базы:

Эквивалентность определений

Все данные выше определения предела функции в точке эквивалентны. [1] Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных.

Вариации и обобщения

Односторонний предел

Односторонний предел числовой функции в точке — это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа). Числовая функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.

Предел вдоль фильтра

Предел функции вдоль фильтра — это обобщение понятия предела на случай произвольной области определения функции. Задавая частные случаи области определения и базиса фильтра на ней, можно получить многие приведённые в этой статье определения пределов.

Пределы на бесконечности

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим. Существуют различные определения таких пределов, но они эквивалентны между собой.

Предел на бесконечности по Гейне

Предел на бесконечности по Коши

\exists \delta = \delta \left( \varepsilon \right) > 0

\forall x \in X \colon x

Окрестностное определение по Коши

Пусть функция определена на множестве , имеющем элементы вне любой окрестности нуля. В этом случае точка называется пределом функции на бесконечности, если для любой её малой окрестности найдётся достаточно большая окрестность нуля, что значения функции в точках, лежащих вне этой окрестности нуля, попадают в эту окрестность точки .

Обозначения

Если в точке у функции существует предел, равный , то говорят, что функция стремится к при стремлении к , и пишут одним из следующих способов:

Если у функции существует предел на бесконечности, равный , то говорят, что функция стремится к при стремлении к бесконечности, и пишут одним из следующих способов:

Если у функции существует предел на плюс бесконечности, равный , то говорят, что функция стремится к при стремлении к плюс бесконечности, и пишут одним из следующих способов:

Если у функции существует предел на минус бесконечности, равный , то говорят, что функция стремится к при стремлении к минус бесконечности, и пишут одним из следующих способов: