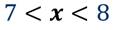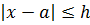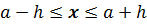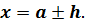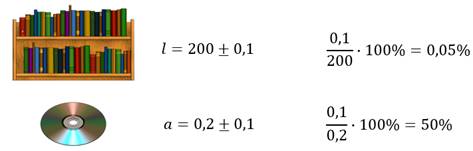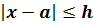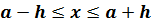Что называют погрешностью приближения

Погрешность и точность приближения

Урок 29. Алгебра 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Погрешность и точность приближения»

При измерении длин отрезков и площадей фигур, при взвешивании тел и других измерениях получаются числа, выражающие эти величины.

Ввиду погрешностей измерения полученные числа являются приближёнными значениями измеряемой величины.

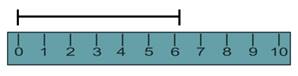
У каждого из вас есть линейка и карандаш. Давайте попытаемся измерить длину карандаша.

Из рисунка видно, что длина карандаша чуть меньше 10 см. Если бы на этой линейке не было миллиметровых делений, то мы бы сказали, что длина карандаша равна 10 см. Но это было бы не совсем точное измерение.

Такую неточность называют погрешностью измерения.

В нашем случае, на линейке есть миллиметровые деления, поэтому мы можем измерить длину карандаша с более высокой точностью – 9,8 см.

Приближённое значение отличается от точного значения в этом случае на 0,2 см. Чтобы узнать, на сколько приближённое значение отличается от точного, надо из большего числа вычесть меньшее, т.е. найти модуль разности точного и приближённого значений. Этот модуль разности называют абсолютной погрешностью.

Абсолютной погрешностью приближённого значения называют модуль разности точного и приближённого значений.

Значение абсолютной погрешности не всегда можно найти. Но обычно известна её оценка сверху – например, при измерении длины отрезка линейкой с сантиметровыми делениями абсолютная погрешность измерения не превышает 1 сантиметра, а при взвешивании на весах с гирями 100 грамм, 200 грамм, 500 грамм и 1 килограмм абсолютная погрешность взвешивания не превышает ста грамм.

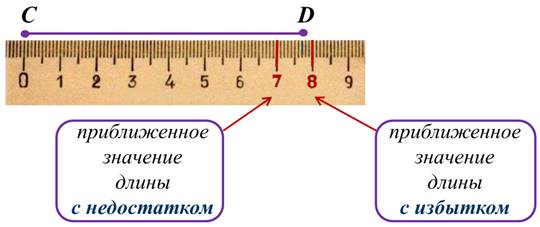
Посмотрите, на слайде изображён отрезок CD.

Его длина расположена между цифрами 7 см и 8 см. Понятно, что 7 см – это приближённое значение длины отрезка CD с недостатком, а 8 см – это приближённое значение длины отрезка CD с избытком.

Если истинную длину отрезка обозначить за х, то получим, что длина отрезка CD удовлетворяет неравенству:

Пусть истинное значение измеряемой величины равно .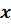

Измерение дало результат .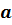

Тогда разность 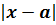– это абсолютная погрешность измерения.

Число 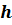называют границей абсолютной погрешности измерения, если выполняется неравенство:

Принято писать

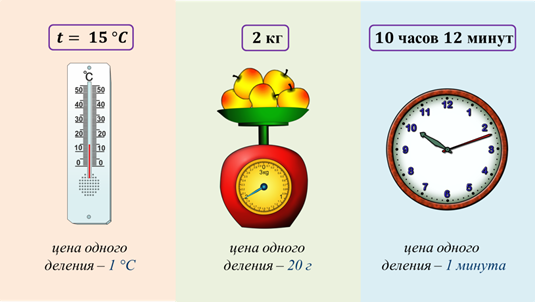
Точность приближённого значения зависит от многих причин. Если приближённое значение получено в процессе измерения, то, конечно же, его точность будет зависеть от прибора, с помощью которого выполнялось это измерение.

Вот, например, комнатный термометр. На нём деления нанесены через один градус. Это даёт возможность измерять температуру воздуха с точностью до 1 градуса. А на весах, у которых цена деления шкалы 20 г, можно взвешивать с точностью до 20 г. Или, к примеру, ещё, механические часы. Цена одного деления, которых 1 мин. По ним можно сказать время с точностью до 1 минуты.

Для оценки качества измерения можно использовать относительную погрешность приближённого значения.

Относительной погрешностью приближённого значения называется отношение абсолютной погрешности к модулю приближённого значения.

Относительную погрешность принято выражать в процентах. В тех случаях, когда абсолютная погрешность приближенного значения неизвестна, а известна лишь его точность, ограничиваются оценкой относительной погрешности.

Например: при измерении (в сантиметрах) длины книжной полки и толщины компакт-диска получили следующие результаты:

Чем меньше относительная погрешность измерения, тем оно точнее.

Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.

Число 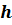называют границей абсолютной погрешности измерения, если выполняется неравенство:

Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения.

Чем меньше относительная погрешность измерения, тем оно

Источник

Относительная и абсолютная погрешность – формула определения, как рассчитать погрешность измерения

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 6%. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для отрезка длиной в 10 см погрешность в 1см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1%.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Источник

Относительная погрешность

Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».

Содержание

Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

Классификация погрешностей

По форме представления

где X_true — истинное значение, а X_meas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина X_meas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

,

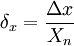
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то X_n определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

По причине возникновения

В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.

Источник

Абсолютная и относительная погрешность

Всего получено оценок: 1760.

Всего получено оценок: 1760.

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Источник

Относительная погрешность. Верные цифры числа

Вычислительная математика. Погрешности. Решение задач

ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ И ЕЕ ГРАНИЦА.

а – приближенное число

Разность х – а между точным числом х и приближенным числом а называется погрешностью приближения.

| х – а | = ∆ – абсолютная погрешность

Отношение абсолютной погрешности к модулю приближенного числа, называется относительной погрешностью

– относительная погрешность является показателем качества данного приближения, и ее часто выражают в процентах %

Граница относительной погрешности больше или равна относительной погрешности:

Если дана граница относительной погрешности, то говорят, что приближение дано с относительной точностью до Ꜫ % и записывают:

х = а (± Ꜫ) или х = а (± Ꜫ %)

В ряде задач границу абсолютной погрешности находят по данной относительной погрешности и модулю приближенного значения величины:

Скорость звука в воздухе 331,63 ± 0,04 м/с

Какое измерение точнее?

– значит скорость света точнее

Дана граница относительной погрешности и необходимо найти границу абсолютной погрешности, используем

Значит границы значений грузоподъемности автомобиля 2,5 ± 0,4 или 2,1 ≤ 2,5 ≤ 2,9

Найдите относительную погрешность в % с точностью до десятых

Решение: границу абсолютной погрешности находим из условия ± 1, значит ∆а=1, далее по формуле

Найдите относительную погрешность в % с точностью до сотых

Радиус Земли (в км): R = 6380 ± 1

Решение: границу абсолютной погрешности находим из условия ± 1, значит ∆а=1, далее по формуле

Найдите относительную погрешность в % с точностью до сотых

Скорость света в вакууме (в км/с):

Решение: границу абсолютной погрешности находим из условия

Диаметр Луны (в км): d = 3476 ± 1

Решение: границу абсолютной погрешности находим из условия ± 1, значит ∆а=1, далее по формуле

Источник