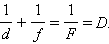Что называют побочной оптической осью

Линза. Виды линз. Фокусное расстояние.

теория по физике 🧲 оптика

Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.

Линза — прозрачное тело, ограниченное сферическими поверхностями.

Какими бывают линзы?

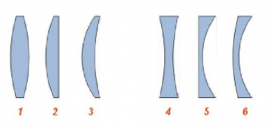
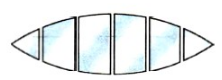
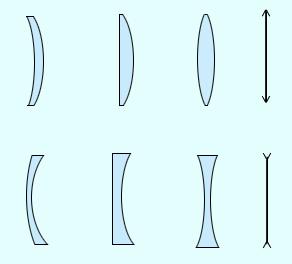
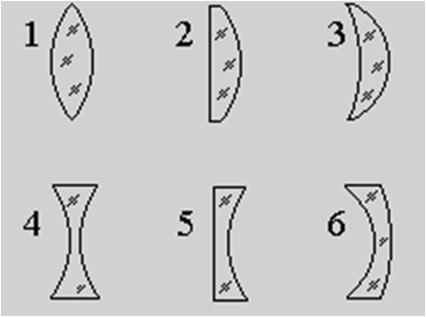
По форме различают следующие виды линз:

Выпуклые линзы тоже имеют разновидности:

Разновидности вогнутых линз:

Тонкая линза

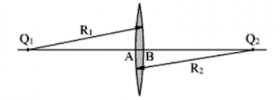
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R₁ и R₂. Такие линзы называют тонкими.

Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.

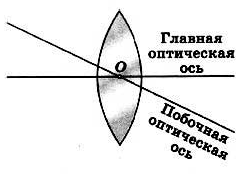
Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O₁O₂).

Оптический центр линзы — точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.

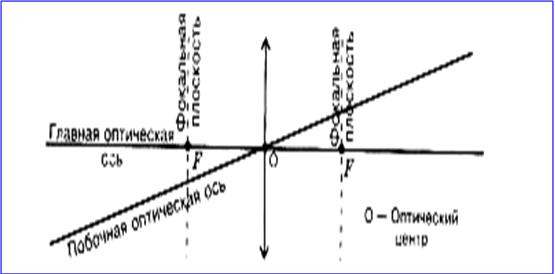
Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.

Изображение в линзе

Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.

Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.

Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.

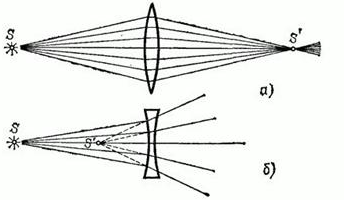
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.

Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.

Собирающая линза

Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.

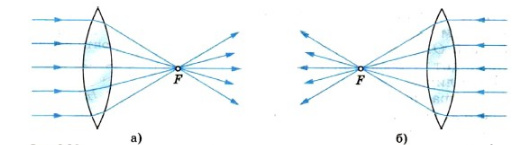
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.

Главный фокус линзы обозначают буквой F.

Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).

В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.

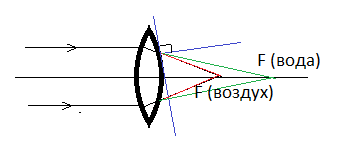
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?

Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.

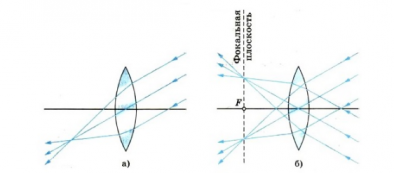
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.

Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.

Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.

Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.

Рассеивающая линза

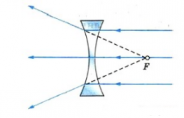
Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.

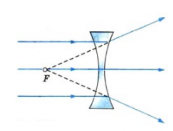
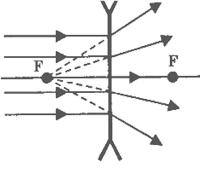
Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.

Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.

Оптическая сила линзы

Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.

Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.

Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:

На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу. Какова приблизительно оптическая сила этой линзы?

Источник

Как сказал.

Жизнь — как вождение велосипеда. Чтобы сохранить равновесие, ты должен двигаться

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Урок 49. Линзы. Оптические приборы.

Лекция 49. Линзы. Оптические приборы.

Отдавая дань исторической традиции, оптическими обычно называют приборы, работающие в видимом свете.

При первичной оценке качества прибора рассматриваются лишь основные его характеристики:

Наименьшее линейное или угловое расстояние между двумя точками, начиная с которого их изображения сливаются, называется линейным или угловым пределом разрешения.

Способность прибора различать две близкие точки или линии обусловлена волновой природой света. Численное значение разрешающей силы, например, линзовой системы, зависит от умения конструктора справиться с аберрациями линз и тщательно отцентрировать эти линзы на одной оптической оси. Теоретический предел разрешения двух соседних изображаемых точек определяется как равенство расстояния между их центрами радиусу первого темного кольца их дифракционной картины.

Увеличение. Если предмет длиной H перпендикулярен оптической оси системы, а длина его изображения h, то увеличение m определяется по формуле:

Увеличение зависит от фокусных расстояний и взаимного расположения линз; для выражения этой зависимости существуют соответствующие формулы.

Основной частью любой оптической системы является линза. Линзы входят в состав практически всех оптических приборов.

Линза – оптически прозрачное тело, ограниченное двумя сферическими поверхностями.

Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.

Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше.

Основные обозначения в линзе:

Прямая, проходящая через центры кривизны O₁ и O₂ сферических поверхностей, называется главной оптической осью линзы.

Оптический центр линзы – точка, сквозь которую световые лучи проходят не преломляясь в линзе.

Главная оптическая ось – прямая, проходящая через оптический центр линзы, перпендикулярно линзе.

Все прямые, проходящие через оптический центр, называются побочными оптическими осями.

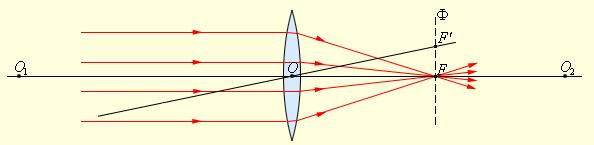
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, расположенных симметрично на главной оптической оси относительно линзы. У собирающих линз фокусы действительные, у рассеивающих – мнимые.

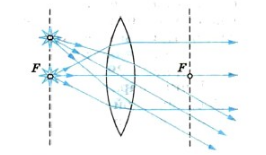
Пучки лучей, параллельных одной из побочных оптических осей, после прохождения через линзу также фокусируются в точку F’, которая расположена при пересечении побочной оси с фокальной плоскостью Ф, то есть плоскостью, перпендикулярной главной оптической оси и проходящей через главный фокус.

Фокальная плоскость – прямая, перпендикулярная главной оптической оси линзы и проходящая через фокус линзы.

Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначаетcя той же буквой F.

Преломление параллельного пучка лучей в собирающей линзе.

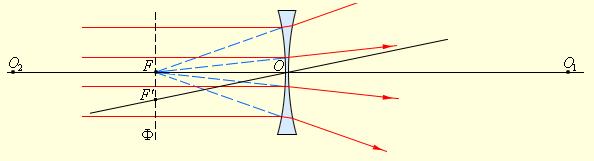
Преломление параллельного пучка лучей в рассеивающей линзе.

Точки O₁ и O₂ – центры сферических поверхностей, O₁O₂ – главная оптическая ось, O – оптический центр, F – главный фокус, F’ – побочный фокус, OF’ – побочная оптическая ось, Ф – фокальная плоскость.

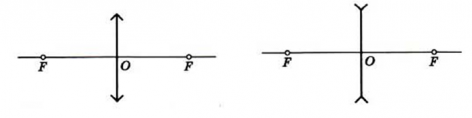
На чертежах тонкие линзы изображают в виде отрезка со стрелками:

собирающая: 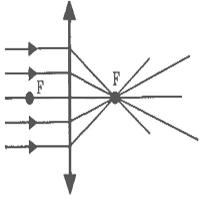рассеивающая:

Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей. Для построения изображения в линзе используют любые два из трех лучей:

Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:

Величину D, обратную фокусному расстоянию называют оптической силой линзы.

Единицей измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = м –1

Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений;
d Подробности Просмотров: 56209

Источник

Построение изображения в линзе

теория по физике 🧲 оптика

Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.

Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.

Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.

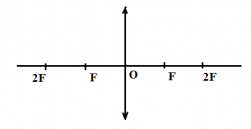
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.

Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.

Построение изображения в собирающей линзе

Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:

Два вида лучей при построении изображений в линзе

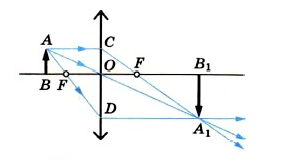
Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).

Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.

На пересечении двух лучей обозначаем точку А₁. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В₁. Изображение предмета при этом — А₁ В_1.

В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.

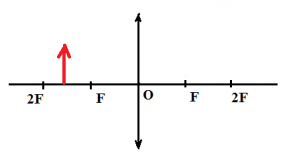
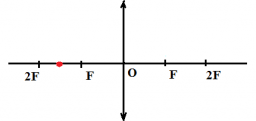
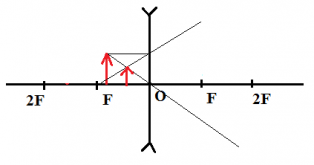
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.

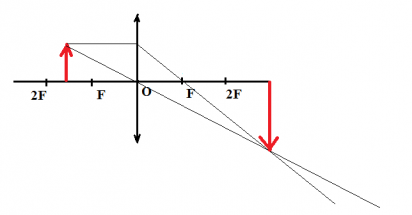
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.

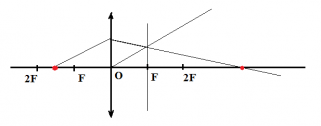
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.

Частный случай — построение изображения точки

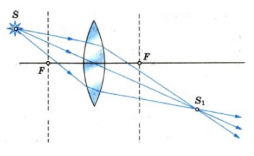
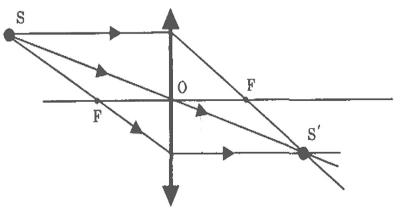
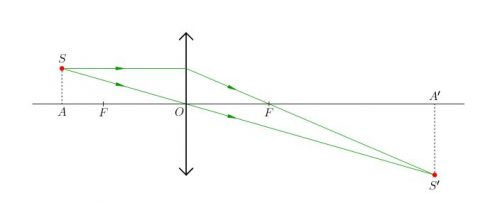
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.

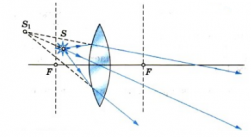
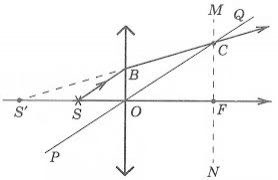
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.

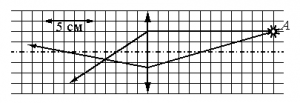
Пример №2. Построить изображение точки, расположенной на главной оптической оси.

Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.

Построение изображения в рассеивающей линзе

Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:

Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).

Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.

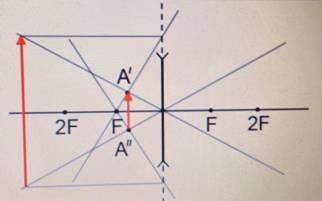
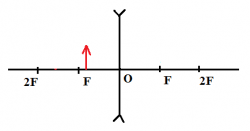
Пример №3. Построить изображение предмета в рассеивающей линзе.

Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.

Построение изображений в плоском зеркале

Плоское зеркало — это плоская поверхность, зеркально отражающая свет.

Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.

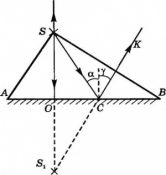
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S₁, которое представляет собой точку пересечения продолжения отраженных лучей.

Таким образом, чтобы получить изображение в плоском зеркале, нужно:

Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.

Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S₁OC равны по стороне и двум углам. Следовательно SO = S₁O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.

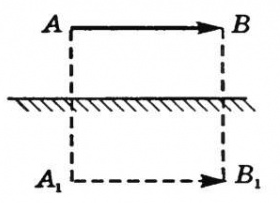
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А₁В₁ соответствует предмету АВ.

Изображение и сам предмет всегда симметричны относительно зеркала.

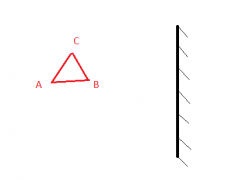
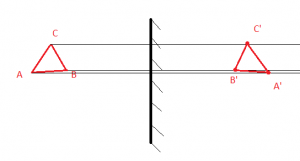
Пример №4. Построить изображение треугольника ABC в плоском зеркале.

Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.

Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Источник