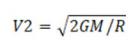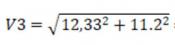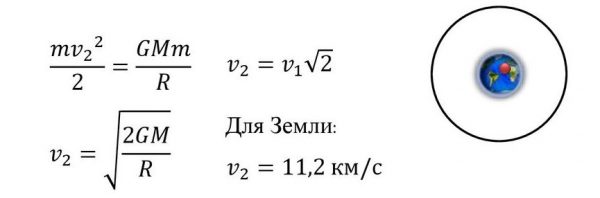Что называют первой и второй космической скоростью каковы их значения
Космические скорости
Если прилагать больше сил при бросании, то он упадет дальше. Отсюда следует, что при отсутствии сопротивления воздуха и при наличии большой скорости тело может даже не приземляться на поверхность. Это говорит о его дальнейшем описывании круговых траекторий, не изменяя высоты относительно земной поверхности.
Первая космическая скорость
Вторая космическая скорость
Для ее нахождения следует произвести вычисление работы, потраченную против сил земного притяжения для соударения с поверхности Земли на бесконечность. При удалении такого тела получаем:
Существует связь между первой и второй скоростями
Квадрат скорости убегания равняется ньютоновскому потенциалу в заданной точке, то есть:
Нужная величина скорости не зависит от направления движения тела. На это влияет вид траектории, по которой происходит удаление от земной поверхности.
Чтобы тело смогло стартовать с поверхности планеты, оно должно обладать второй космической скоростью при малом значении h и большом значении гравитационной силы. Как только ракета начнет удаляться от Земли, гравитационная постоянная будет уменьшаться вместе со значением, необходимым для убегания кинетической энергии.
Третья космическая скорость
Еще в СССР были достигнуты космические скорости.
Дано:
Решение
Значение g принимает ускорение свободного падения на Юпитере.
Значение m определено как масса спутника, а М – масса самой планеты.
Получаем, что из уравнения ( 2 ) найдем ускорение свободного падения для планеты из
Космические скорости.
Первая космическая скорость – скорость, которую необходимо сообщить телу, чтобы оно двигалось вокруг Земли по круговой орбите с постоянной скоростью под действием силы тяжести, т. е. стало искусственным спутником.
Спутником Земли может стать тело любой массы, лишь бы ему была сообщена достаточная скорость. Для спутника, запускаемого вблизи Земли (h = 0) скорость равна:
где G – гравитационная постоянная, M – масса Земли, R – радиус Земли. Эта формула является формулой расчета первой космической скорости при запуске спутника, т. е. той горизонтальной скорости, которую сообщают телу вблизи поверхности Земли, чтобы оно стало ее спутником.
Поскольку 


Подставив в эту формулу значения g = 9,8 м/с 2 и R = 6,4∙10 6 м, получим υ ≈ 8 км/с.
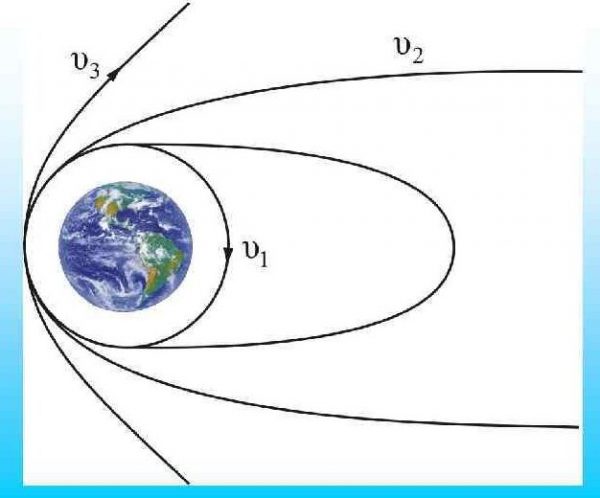
Искусственный спутник запускают при помощи ракеты-носителя, которая поднимает спутник на высоту порядка 300 км (на этой высоте почти не сказывается сопротивление атмосферы) и придает ему горизонтальную скорость υ1. Спутник, отделившись от ракеты, продолжает движение в гравитационном поле Земли. Если телу придать бо´льшую скорость, его движение будет происходить по эллиптической орбите. По мере увеличения начальной скорости, приданной телу при запуске, его орбита будет вытягиваться, пока не превратится в незамкнутую кривую – параболу.
Второй космической (параболической) скоростью называют скорость, которую надо придать телу у поверхности Земли, чтобы оно ее покинули, двигаясь по параболической траектории. Эта скорость в 
Космические скорости
4 октября 1957 года советская ракета носитель Р7 вывела на низкую земную орбиту аппарат под кодовым названием ПС-1. Именно с этого момента начинается отсчет космической эры. Чтобы космический аппарат смог стать спутником нашей планеты, ракете пришлось разогнать его до огромной скорости – почти 28.5 тысячи км/час (7.9 км/с). Эта скорость называется первой космической.
Что такое космическая скорость
Впервые понятие 1-й космической скорости (V1) ввел в обиход А.А. Штернфельд в своей работе «Введение в космонавтику» в 1934г. Кстати из этой же монографии пришел и термин космодром. Именно благодаря этому ученому, в СССР (а позже в России) люди, летающие на орбиту, стали называться космонавтами, а не астронавтами как в США.
Космические (с приставками 1–4) называются скорости, при достижении которых происходит качественное изменения в движении космических объектов в гравитационных полях небесных тел и их систем.
Они различны для различных небесных объектов, и обеспечивают ракете, стартующей с планеты возможность:
Величины эти зависят от массы небесного тела и удаления от его центра.
Минимальная скорость, которую надо сообщить объекту, чтобы центробежная сила уравновешивала силу тяжести, называется круговой или первой космической.
Вычисляется по формуле 1:
G – гравитационная постоянная (6.67430(15)·10 −11 Н·м²·кг −2 ).
M – масса центрального тела, для Земли M = 5.97·10 24 кг.
R – расстояние от центра до объекта, для поверхности Земли R = 6,371·10 6 м.
Для поверхности Земли, V1 составляет 7,91 км/с.
Если речь идет об объекте, находящемся на некотором расстоянии над поверхностью, то скорость немного уменьшится (за счет увеличения R). Так для орбиты в 100 км над поверхностью Земли она равна 7 844 м/с, а на высоте 300 км — 7 726 м/c.
Это скорость (наименьшая), до которой надо разогнать космический аппарат, чтобы он мог полностью преодолеть гравитационное поле планеты. Другое название – скорость убегания или параболическая.
Определяется по формуле 2:
Как видно из формулы, параболическая скорость больше круговой в 1.41 раза. Для Земли она равна 11.2 км/с, для Марса 5.04 км/с, для Солнца это уже 618.7 км/с.
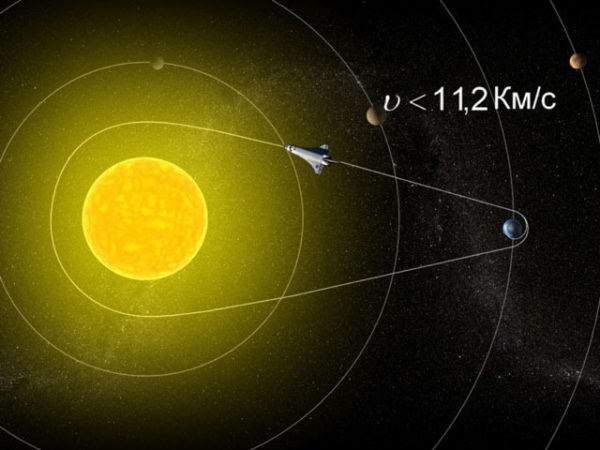
Если скорость объекта больше круговой, но меньше параболической, то он движется вокруг солнца по эллиптической орбите. Чем выше скорость, тем более вытянутый эллипс.
Это скорость, необходимая для того, чтобы покинуть пределы солнечной системы навсегда. Являясь параболической в отношении нашего Солнца, одновременно будет круговой по отношению к центру тяжести Млечного пути (нашей галактики).
Аппарат стартует с нашей планеты и уже обладает скоростью Земли (вычисляется по формуле с учетом расстояния до Солнца равного 150 млн. км) равной 29.77 км/с.
Для отрыва от центрального светила – V2 для Солнца на орбите Земли нужно 42.09 км/с. То есть не хватает 12.3 км/с.
Кроме того, аппарат должен потратить топливо для полного преодоления земной гравитации. V2 для Земли = 11.2 км/с.
В итоге, третья космическая скорость составит:
= 16.65 км/с
Это скорость, имея которую можно безвозвратно покинуть нашу галактику. Из-за отсутствия точных данных о распределении массы во Вселенной подсчитана только приблизительно. Формула для вычисления скорости убегания из нашей галактики:
По сегодняшним оценкам V4 в районе нашего светила составляет примерно 550 км/с. При этом скорость с которой наша звезда летит вокруг центра Млечного пути составляет 220 км/с.
Пятая скорость –можно ли покинуть нашу вселенную?
По аналогии с официально используемыми четырьмя космическими скоростями некоторые авторы ввели понятие пятой. В их понимании это скорость, которую надо развить, чтобы навсегда улететь из нашей Вселенной. Красиво, но наука пока не знает, сколько существует вселенных – одна или бесчисленное количество. Что представляет пространство вне Вселенной, какие законы там действуют. Есть ли там гравитация, которая и определяет значения космических скоростей (V1 – V4) – неизвестно.
Скорость света
Скорость света, или скорость распространения электромагнитных волн в вакууме составляет 299 792.5 км/с.
От Земли до Луны он долетит за секунду с небольшим. Для преодоления расстояния до Солнца потребуется 8 минут.
Астрономы, наблюдающие за звездами, меряют расстояния световыми годами. Один световой год – расстояние которое преодолевает свет за 365.25 суток. В более привычных нам единицах – это 9460 миллиардов км. До ближайшей к нам звезды (Проксима Центавра) – 4.25 св.г. Размер нашей галактики – 100 тысяч св. лет.
Скорость света является предельной, материальные объекты не могут двигаться быстрее. При движении со скоростями близкими к скорости света возникают релятивистские эффекты. Время для пассажиров звездолета течет медленнее. При достижении скорости света (гипотетически) оно полностью останавливается.
Космические скорости
«Поехали!»
В 1957 году работа советских учёных, конструкторов, инженеров, рабочих, во главе с Сергеем Павловичем Королёвым, увенчалась блестящей победой: 4 октября они вывели на орбиту первый в истории искусственный спутник Земли. А 12 апреля 1961 года отправили в первый космический полёт человека — Юрия Алексеевича Гагарина. На весь мир прозвучало знаменитое гагаринское «Поехали!», и человечество вступило в космическую эру.
Космическая тематика стремительно вошла в моду. Естественно, появились новые темы и понятия — ракеты, скафандры, невесомость, первая космическая скорость, вторая космическая скорость. Все мальчишки нашего поколения в мечтах примеряли скафандр космонавта. О невесомости мы поговорим в другой раз, а пока рассмотрим космические скорости.
Что известно о космических скоростях простым людям
На телевидении есть передача, в которой весёлый молодой человек бегает по улицам и задаёт прохожим разные вопросы. За правильный ответ он вручает 1000 рублей. Однажды он задал такой вопрос: «Какую скорость надо развить, чтобы оторваться от Земли?» Первый встречный ответить не смог, и ведущий буквально клещами вытащил из второго ответ, который был признан правильным: «Вторую космическую».
Увы, молодой человек ошибся. Вернее, ошибся не он, а редакторы, придумывающие вопросы и ответы к ним. Точно так, как и редакторы, считают почти все, кто хоть отдалённо слышал про существование первой и второй космических скоростей.
На самом деле, чтобы оторваться от Земли, подходит любая скорость. Уже когда ребёнок подпрыгивает, он отрывается от Земли. Пусть ненадолго, но отрывается. И вообще, до Луны или до другого космического объекта можно добраться с любой скоростью. Для этого надо немного разогнаться, а потом поддерживать силу тяги двигателя, равную силе земного притяжения, и вы будете «бороздить просторы Вселенной» с постоянной скоростью. Более того, если представить, что какой-то чудак сумел построить лестницу до Луны, то вы сможете подняться туда просто пешком. Примерно так, как вы поднимаетесь к себе домой на третий этаж, только гораздо дольше.
А как же космические скорости? Космические скорости подразумевают, что ракета, достигнув их, дальше летит к намеченной цели по инерции, с неработающим двигателем. Это только в мультфильмах про космические путешествия показывают летящие ракеты с работающим двигателем. Но это исключительно для создания иллюзии движения.
Если же в реальных условиях двигатель у ракеты будет работать постоянно, то даже для полёта на Луну потребуется такое количество топлива, что его ни одна ракета не осилит.
Постреляем
Первая космическая скорость
Первая космическая скорость — это скорость, с которой надо горизонтально запустить объект, чтобы он стал вращаться вокруг Земли по круговой орбите.
Чем больше высота, с которой мы запускаем объект, тем меньше эта скорость. Например, Международная космическая станция летает на высоте 400 км со скоростью 7,6 км/с, а Луна — на расстоянии 384 500 км от Земли со скоростью 1 км/с. «Нулевой» высоте соответствует скорость 7,9 км/с, что обычно и называют первой космической скоростью.
Точно так же Земля вращается вокруг Солнца почти по круговой орбите со скоростью ≈ 30 км/с. Это и есть первая космическая скорость относительно Солнца на таком расстоянии от него.
Если скорость спутника чуть больше первой космической для его высоты, его орбита будет эллипсом. Все спутники вокруг Земли и планеты вокруг Солнца движутся именно по эллипсам. И орбиты комет — тоже эллипсы, только очень вытянутые, так что кометы улетают по ним «в даль тёмную», лишь изредка возвращаясь к Солнцу «погреть бока».
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Вторая космическая скорость
Вторая космическая скорость — наименьшая скорость, которую необходимо придать космическому аппарату для преодоления притяжения планеты и покидания замкнутой орбиты вокруг неё.
Предполагается, что аппарат не вернётся на планету, улетит в бесконечность. На самом деле тело, имеющее около Земли такую скорость, покинет её окрестности и станет спутником Солнца. Вторая космическая скорость в \(\sqrt <2>≈ 1<,>4\) раза больше первой космической.
Третья космическая скорость
Третья космическая скорость — минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть притяжение не только Земли, но и Солнца, и покинуть пределы Солнечной системы.
Космические достижения
Первый искусственный спутник Земли был шариком диаметром 58 см и передавал только звуковой сигнал «бип-бип-бип». Но первая космическая скорость была достигнута! А всего через год, 2 января 1959 года, космический аппарат «Луна-1» полетел, естественно к Луне, со второй космической скоростью.
Пока с наибольшей скоростью 16,26 км/с покидала Землю автоматическая межпланетная станция «Новые горизонты», запущенная в США 19 января 2006 года. Относительно Солнца её скорость составляла 45 км/с — благодаря тому, что запускалась она в сторону движения Земли по орбите.
Конические сечения
Вернёмся к движению тела вокруг одного источника притяжения, например Солнца. Если тело запустить с первой космической перпендикулярно направлению на Солнце, оно полетит по окружности. Если запустить его в любом направлении, только не на само Солнце, со скоростью меньше второй космической, орбита будет эллипсом. При запуске со второй космической получится парабола. Если запустить с ещё большей скоростью, получится гипербола.
Эти кривые можно увидеть, пересекая конус плоскостью. Если ось конуса перпендикулярна плоскости, в пересечении получится окружность. Будем постепенно менять угол наклона плоскости к оси конуса. Линия пересечения превращается в эллипс, причём чем больше угол наклона, тем более вытянутым получается этот эллипс. Продолжим наклонять секущую плоскость до тех пор, пока она не станет параллельной одной из касательных плоскостей конуса. В этот момент линия пересечения — парабола. Наклоним ещё — получится гипербола.
Художник Мария Усеинова
1 Подробнее об этом читайте в «Квантике» №11 за 2016 год, с. 2–5.
Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
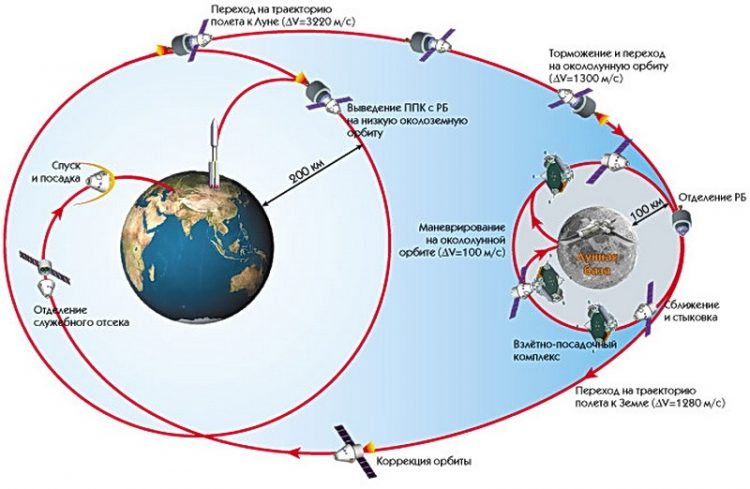
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
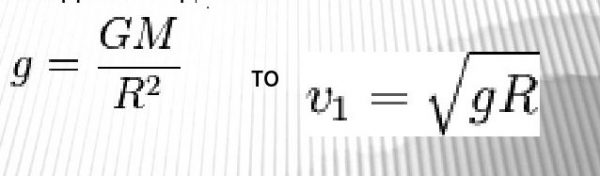
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.