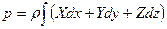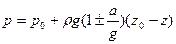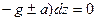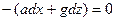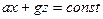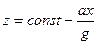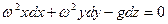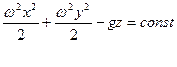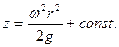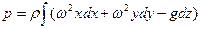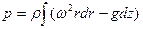Что называют относительным равновесием жидкости

Относительное равновесие жидкости

В движущихся сосудах

Движение сосуда с жидкостью прямолинейно в

Произвольном направлении с постоянным ускорением

Движение сосуда с жидкостью вертикально вниз

С постоянным ускорением

Равномерное вращение цилиндрического сосуда

С жидкостью вокруг вертикальной оси

Равновесие жидкости в поле центробежных сил

При нулевой или слабой гравитация

Относительным равновесием жидкости называется такой случай ее движения, при котором вся масса жидкости движется как твердое тело, а отдельные ее частицы не смещаются одна относительно другой. Например, представим, что некоторый замкнутый сосуд с жидкостью движется с постоянной скоростью (или постоянным ускорением) в любом направлении, тогда с этой же скоростью (или ускорением) движется также и каждая частица жидкости. Очевидно, что рассматриваемая масса жидкости будет неподвижна в координатной системе, связанной с движущимся резервуаром. Такое движение жидкости представляет собой относительное ее равновесие.

При относительном покое свободная поверхность жидкости и прочие поверхности уровня могут существенно отличаться от поверхностей уровня при покое жидкости в неподвижном сосуде, т.е. от горизонтальной плоскости. При определении формы и положения свободной поверхности жидкости, находящейся в относительном покое, следует руководствоваться основным свойством всякой поверхности уровня, которое заключается в следующем: равнодействующая массовых сил всегда действует нормально к поверхности уровня. В самом деле, если бы равнодействующая массовая сила действовала под некоторым углом к поверхности уровня, то касательная составляющая этой силы вызывала бы перемещение частиц жидкости вдоль поверхности уровня.

Рассмотрим три практически наиболее интересных случая относительного покоя жидкости:1) движение сосуда прямолинейно в произвольном направлении; 2) движение сосуда по вертикали; и 3) вращательное движение относительно вертикальной оси.

Движение сосуда с жидкостью прямолинейно в

Источник

Основные законы гидростатики. Абсолютное и относительное равновесие жидкости

Закон Паскаля р=р₀+ρg(z₀-z)= р₀+ ρgh, Па. – основное уравнение гидростатики несжимаемой жидкости, также: [**] р/(ρg)+ z = р₀/(ρg) + z₀ =const.

р, Па – давление в произвольной точке рассматриваемой жидкости на высоте z, (м); р₀ – давление в исходной точке отчёта на высоте z₀, (м); ρ – плотность жидкости (кг/м 3 ); z – геометрическая или нивелирная высота (м). (р/(ρg)+ z) – гидростатическая высота (м). Из [**] следуют выводы: давление р в любой точке покоящейся жидкости складывается из давления р₀ на свободную поверхность и давления ρgh столба вышележащей жидкости. [РИСУНОК]

Из этого вывода вытекает содержание 1 – го основного закона гидростатики, закона Паскаля: «Давление, приложенное к покоящейся жидкости передаётся во все ее точки одинаково».

Из формулы [**] вытекают также следующие выводы: 1. Давление в жидкости при ρ = const нарастает линейным образом с увеличением глубины погружения. Скорость этого нарастания пропорциональна плотности жидкости. 2. Поверхности уровня р = const параллельны свободной поверхности жидкости при z₀. [РИСУНОК].

Абсолютное и относительное равновесие жидкости. Наука, изучающая жидкость в состоянии покоя или состоянии абсолютного равновесия называется гидростатикой. А гидродинамика изучает движущуюся жидкость. Под абсолютным равновесием понимают равновесие жидкости относительно сосуда, покоящегося относительно земли либо движущегося прямолинейно, равномерно.

Под равновесием жидкости принято понимать в гидростатике постоянство формы её объёма. При этом имеется в виду, что любой выделенный объём сохраняет своё местоположение и не перемещается относительно других объёмов.

Сказанное означает, что в жидкости, находящейся в состоянии равновесия отсутствуют касательные напряжения, и внутри такой жидкости действуют только массовые силы(силы тяготения), а также силы, приложенные к поверхности внешнего характера.

Относительное равновесие – равновесие жидкости относительно сосуда, движущегося относительно земли с постоянным ускорением, либо вращающегося с постоянной скоростью относительно какой-либо оси.

Рассмотрим жидкость в состоянии абсолютного равновесия, мысленно выделив внутри сосуда объём. Поскольку данный объём неподвижен, то силы, действующие на этот объём уравновешены. Таких сил 2: сила тяжести R_T жид = ρж*g*V, эта сила уравновешивается поддерживающей силой R_п = ρж*g*V, которая ей же равна, поэтому V не движется. Поскольку др. сил нет, то и равнодействующая этих 2-х сил равна нулю, если теперь представить, что вместо объёма жидкости поместить какое – либо тело, с плотностью ρ_Т, то при этом поддерживающая сила изменяться не может. А сила тяжести R_T = ρ_т*g*V и она зависит от плотности. Рисунок соответствует случаю, когда ρ_т

Источник

Относительное равновесие жидкости

Относительным равновесием жидкости называется такое состояние, при котором каждая ее частица сохраняет свое положение относительно твердой стенки движущегося сосуда. При относительном равновесии рассматриваются две задачи: характер распределения давления и форма поверхности уровня (равного давления). Решаем эти задачи опять же используя полученное нами на прошлой лекции уравнение для определения гидростатического давления

При р=const Xdx+Ydy+Zdz=0 (3.4)

В общем случае любое сложное движение сосуда с жидкостью можно представить в виде суммы трех движений: поступательного по вертикали и горизонтали и вращательного.

1) Движение по вертикали с постоянным ускорением а.

Проекции массовых сил на координатные оси будут: X=0, Y=0, Z=. Знак «-» соответствует равноускоренному подъему резервуара, «+»- спуску.

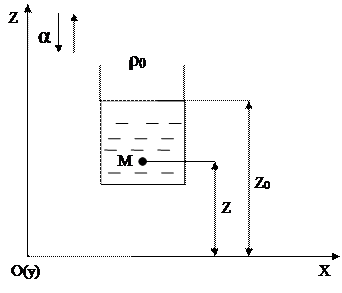
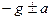
Характер распределения давления получим следующий

,

+С,

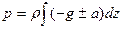
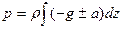
где С- постоянная интегрирования, определяемая из граничных условий на свободной поверхности Z=Z0 и P=P0/

Составим уравнение поверхности уровня

(

Если g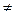а, то dz=0, z=const, т.е. поверхности равного давления представляют собой горизонтальные плоскости.

2) Горизонтальное перемещение резервуара с жидкостью с постоянным ускорением а.

В этом случае X=-a, Y=0, Z=-g.

Закон распределения давления получим

.

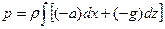
После интегрирования с учетом граничных условий X=X0, Z=Z0, P=P0 получим закон распределения давления в следующем виде

.

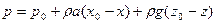
Т.о. распределение давления в жидкости подчиняется основному закону гидростатики для любой фиксированной вертикали.

Поверхность равного давления определится уравнением

Т.о. поверхностями равного давления будут плоскости, углы наклона которых к горизонтальной плоскости определяются угловым коэффициентом, равным –a/g.

3) Вращение цилиндрического сосуда с жидкостью с постоянной угловой скоростью .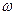

Поверхность равного давления определяется уравнением

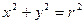
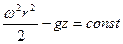
Или учитывая, что получим

.

Т.о. при вращении сосуда с жидкостью вокруг вертикальной оси поверхностями равного давления будет семейство параболоидов вращения, осью которых является ось Oz.

Закон распределения давления получим

После интегрирования с учетом граничных условий r =0, z=z0, p=p0 получим закон распределения давления:

.

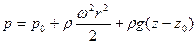
Это уравнение показывает, что распределение давления подчиняется линейному закону для любой фиксированной круглоцилиндрической поверхности.

Поможем написать любую работу на аналогичную тему

Источник

Относительное равновесие

Относительным равновесием жидкости называется такой случай ее движения, при котором отдельные ее частицы не сме­щаются одна относительно другой и вся масса жидкости дви­жется как твердое тело. Например, вообразим, что некоторый замкнутый резервуар (наполненный жидкостью) движется с по­стоянной скоростью (или постоянным ускорением) в любом на­правлении и с этой же скоростью (или ускорением) движется также и каждая частица жидкости, находящейся в резервуаре. Очевидно, что рассматриваемая масса жидкости будет неподвиж­на в координатной системе, связанной с движущимся резервуа­ром. Такое движение жидкости представляет собой относитель­ное ее равновесие.

Рассмотрим два практически наиболее интересных случая: движение по вертикали и вращательное движение относительно вертикальной оси.

1. Движение по вертикали

Допустим, что открытый резервуар вместе с находящейся в ней жидкостью движется в вертикальном направлении сверху вниз с некоторым постоянным ускорением j, меньшим ускорения свободного падения g или равным ему (рис. 1.14).

Определим вид поверхности уровня и закон распределения гидростатического давления. Заметим предварительно, что, со­гласно принципу даламбера, при любом движении тела можно пользоваться уравнениями статики, если к системе действую­щих сил прибавить силы инерции (они направлены в сторону, противоположную направлению движения). Такая система сил будет уравновешена, и тело можно считать находящимся в рав­новесном состоянии.

Следовательно, мы можем воспользоваться уравнением поверхности уровня:

Чтобы написать уравнение поверхности уровня для данного случая, определим X, Y и Z. Ускорениями действующих сил бу­дут ускорения свободного падения g (9,81 м/с 2 ) и ускорение сил инерции j_и. Оба ускорения направлены параллельно оси Oz. Сле­довательно, проекции этих ускорений на оси хну равны нулю: Х=0 и Y=0, а

Итак, уравнение поверхности уровня в дифференциальной форме примет следующий вид:

Если

Если j=g,

то =1 и тогда dz может быть и не равным нулю, следовательно, форма свободной поверхности может быть произвольной.

То есть при падении с ускорением g (свободное падение) жидкость в невесомости, значит форма поверхности произвольная.

Определим закон распределения Гидростатического давления.

2. Статическое вращение жидкости

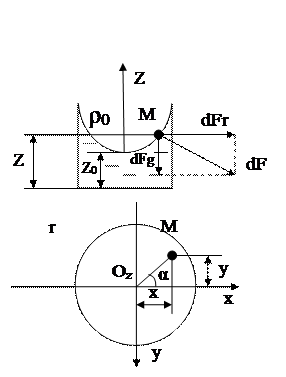
Предположим, что ци­линдр с водой, налитой до глубины zо, приведен во вращатель­ное движение вокруг вертикальной оси Oz с угловой скоростью ω, с-1 (рис. 2.15).

Вращающиеся стенки цилиндра приведут во вращательное движение ближайшие к стенкам слои жидкости, а затем, вслед­ствие вязкости жидкости — и всю ее массу. По истечении извест­ного времени все частицы жидкости будут вращаться примерно с одной и той же угловой скоростью ω.Допустим, что такой момент времени наступил.

Определим форму поверхности уровня и, в частности, свободной поверх­ности.Как и в первой задаче, будем исходить из общего дифферен­циального уравнения поверхности уровня

Так как движение симметрично относительно оси вращения, то рассмотрим равновесие частиц жидкости, расположенных в плоскости координат xOz, вращающейся с угловой скоростью ω. Как и в предыдущей задаче, объемными силами будут силы земного тяготения и силы инерции. Последняя представляет собой центробежную силу, направленную параллельно оси Ох и в сторону от оси вращения.

В точке М на расстоянии х от оси Oz линейная скорость ча­стицы u=хω, поэтому для нее центробежное ускорение

и следовательно полное ускорение внешних объемных сил:

Очевидно, что в данном случае:

Делая подстановку получим:

и после интегрирования

что представляет собой уравнение параболы с вершиной на оси Oz в точкеА, имеющей координату z_i=h.

Поскольку уравнение симметрично относительно оси Oz, то поверхность уровня будет представлять собой парабо­лоид вращения.

Запишем закон распределения давления:

В качестве примеров можно решить задачи 1.2, и 1.3 на странице 50

Уч. Альтшуль – Гидравлика и Аэродинамика.

2.12 Равновесие Газов

Источник

Относительное равновесие жидкости.

В буровой практике находят применение гидравлические аппараты, в которых жидкость вращается в цилиндрических сосудах, например, в гидроциклонах и центрифугах.

В центрифуге (а с некоторым приближением и в гидроциклонах) жидкость вращается с постоянной для всех частиц жидкости угловой скоростью. В подобных случаях говорят, что жидкость находится в относительном равновесии по отношению к стенкам вращающегося сосуда или одних частиц жидкости по отношению к другим.

В названных устройствах жидкость вращается с такими угловыми скоростями, что созданное этим вращением силовое поле (после центробежных сил) оказывается более напряженным, чем поле земного тяготения, причем настолько, что последним можно пренебречь.

Воспользуемся дифференциальным уравнением гидростатики

В соответствии с ранее сказанным

Центробежную силу направляем вдоль оси Ох, тогда

В результате получаем дифференциальное уравнение:

.

Постоянную интегрирования найдем исходя из граничных условий: при x=r_о р=р_о, (например на свободной поверхности).

; .

Подставив найденное С в уравнение, находим:

. (1.18)

Если жидкость полностью заполняет вращающейся сосуд или сама вращается в неподвижном сосуде (например, в гидроциклоне), то r_о=0, то

. (1.19)

Определим угловую скорость вращения жидкости:

.

Радиус центрифуги х=0,2 м. Тогда

.

Формула (1.19) применима для определения давления на стенки скважины, возникающего при вращении, например, алмазного долота.

2. Особенности гидростатики вязкопластичных жидкостей (ВПЖ).

Общие замечания.

Системы, обладающие тиксотропными свойствами, создающими тиксотропную структуру, как ранее отмечалось, обладают свойствами твердого тела, обладают некоторой, пусть небольшой, начальной прочностью, оцениваемой величиной статического напряжения сдвига θ. Значение θ зависит от времени, в течении которого вязкопластичная жидкость находилась в покое. Для разных буровых растворов, которые часто, особенно глинистые растворы обработанные «старыми» реагентами-стабилизаторами, такими как УЩР, ТЩР, КССБ, КМЦ и др., относятся, как указывалось выше, к реологически нестационарным системам. Для них соотношение τ_о и θ может быть самым различным. При небольших тиксотропных свойствах θ >τ_о (этот случай показан на рис. В.2).

Предположим, что скважина (рис. 2.1) заполнена вязкопластичной жидкостью, подчиняющейся модели Шведова-Бингама с реологическими показателями τ_о, η и статическим напряжением сдвига (начальной прочностью) θ. Давление, создаваемое такой жидкостью на стенки скважины, в том числе и на продуктивные пласты, можно определять по формулам, полученным ранее для вязкой, ньютоновской, жидкости:

Предположим теперь, что скважина вскрыла пласт, давление которого р_пл>р, т.е. р_пл>ρgL.

Если бы в скважине была не вязкопластичная, а вязкая жидкость, то сразу бы началось движение жидкости из скважины, т.е. нефте-, водо-, или газопроявление. Совсем другое дело, когда в скважине вязкопластичная жидкость. Чтобы сдвинуть ее, необходимо приложить к ней давление, превышающее р на величину, достаточную для преодоления сил сопротивления, вызванных «к жизни» наличием статического напряжения сдвига θ.

Опишем предельное состояние равновесия между внешней силой, выталкивающей жидкость из скважины, диаметром D, длинной L (рис. 2.1) и силами сопротивления, препятствующими такому выталкиванию:

,

. (2.1)

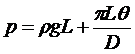
Следовательно, только в том случае, если р_пл превысит на величину (pLq /D)гидростатическое давление столба бурового раствора, скважина начнет «проявлять».

2.2. Расчет «пусковых» давлений на насосах.

Расчет сводится к решению задачи: какое давление нужно создать в спущенных в скважину трубах, чтобы вывести вязкопластичную жидкость, которой заполнены трубы и скважина, из состояния покоя.

Показанная на рис. 2.2 система труб представляет собой систему сообщающихся сосудов, один из которых образован стенками скважины и наружными стенками труб, а другой – самой трубой. Примем, что колонна труб состоит из секций труб двух размеров d₁ и d₂. Длина секции соответственно l₁ и l₂. Диаметр скважины – D. Длина колонны – L_к. Внутренний диаметр труб d_1в и d_2в.

Усложним задачу. Договоримся, что колонна труб заполнена жидкостью с ρ_в, θ_в, а заколонное – с параметрами ρ_кп, θ­_кп, причем ρ_кп>ρ_в. Такая ситуация создается, например, в конце цементирования обсадной колонны, когда в кольцевом пространстве за трубами находится еще не начавший застывать цементный раствор, а в колонне – продавочная жидкость.

Условие предельного равновесия вязкпластичной жидкости в этом случае запишется следующим образом.

где р_о – «пусковое» давление;

р_1в и р_2в – давления, необходимые для преодоления сил, вызванных напряжениями θ в трубах;

Последний член уравнения – это давление, необходимое для уравновешивания давления, вызванного разной плотностью жидкости в трубах и в заколонном (затрубном) пространстве.

;

.

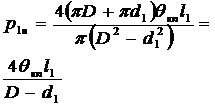
Аналогично для второй секции:

; .

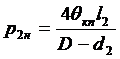
Подставив эти выражения в уравнение, найдем р_о:

. (2.2)

При i –том числе секций:

. (2.3)

. (2.4)

1046273 Па = 1,05 МПа.

Из этого следует, что буровой раствор (при промывке скважины, а не при цементировании) будет находиться в состоянии покоя до тех пор, пока давление на насосах не превысит 1,05 МПа.

Для практики бурения представляет большой интерес и другая задача, обратная рассмотренной: определение «остаточного» давления на насосах р_ост после того, как насосы плавно остановлены без открывания пусковой задвижки. Дело в том, что при этом давление на насосах никогда не опускается до нуля сразу. Если считать, что жидкость подчиняется модели Бингама, то будет справедливо признать, что в данном случае р_ост является величиной, эквивалентной не θ, а τ_о.

, (2.5)

. (2.6)

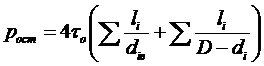
Формулой (2.6) можно воспользоваться для ориентировочного определения τ_о, когда нет приборов для измерения реологических параметров, а формулой

, (2.7)

полученной из формулы (2.4), – для оценки СНС. Сравнение θ и τ_о даст оценку степени реологической нестационарности применяемой промывочной жидкости.

2.3. Определение высоты перепада уровней вязкопластичной жидкости в трубах и заколонном пространстве при спуске
и подъеме колонны труб.

Скважина и спущенная в нее колонна нефтепромысловых труб (бурильные, обсадные и насосно-компрессорные) образуют систему сообщающихся сосудов, где одним из сосудов является колонна, а другим заколонное пространство. Если бы скважина была заполнена ньютоновской жидкостью, например, водой, то при равенстве плотностей жидкостей в обоих «сосудах», уровни жидкости в них совпадали бы. Несколько иначе обстоит дело, когда скважина заполнена вязкопластичной жидкостью (ВПЖ), например глинистым раствором.

При медленном спуске (рис. 2.3) колонны в скважину (медленном для того, чтобы избежать инерционных сил и влияния гидродинамических факторов) уровень жидкости в трубах будет опускаться вместе с колонной и после остановки колонны может оказаться ниже устья скважины на величину h.

Найдем наибольшее значение h, при котором ВПЖ в скважине еще может находиться в состоянии покоя, не перетекая из заколонного пространства в трубы (после спуск) или наоборот (после подъема). Обозначим диаметр скважины через D, внутренний диаметр труб – d_в, наружный диаметр – d_н, длину колонны труб в скважине – L_к.

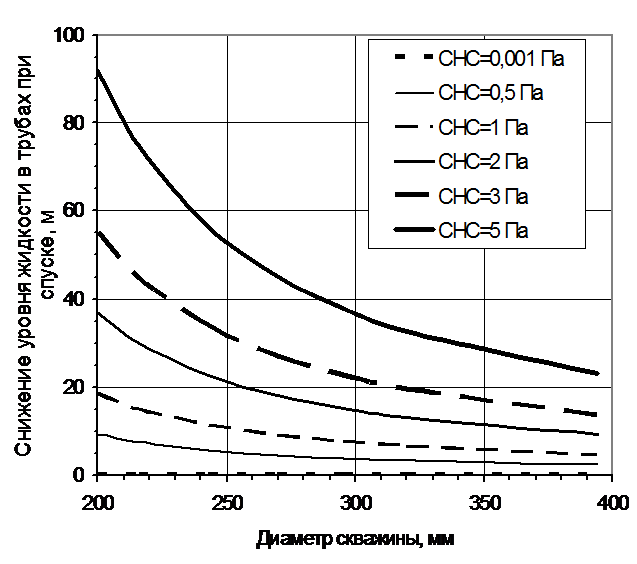
Рис. 2.4. Влияние диаметра скважины и СНС бурового раствора на снижение уровня жидкости в бурильной колонне диаметром 127 мм длиной 3000 м после ее спуска.

Условие предельного равновесного состояния выразится уравнением:

.

Выразим h через другие величины:

. (2.8)

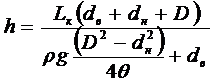
Подставив исходные данные в формулу (2. 8), получим h= 75 м.

Итак, если скважина заполнена до устья, то в трубах жидкость может опускаться (после спуска труб) от устья на десятки метров. С уменьшением L_к величина h снижается пропорционально изменению L_к. Из формулы (2.8) видно, что на величину h основное влияние оказывают L_к и θ. Положительно влияет и увеличение d­_в и D.

Формула (2.8) применима и для определения разности уровней h в трубах и заколонном пространстве после завершения подъема колонны (в этом случае в трубах жидкость поднимается над устьем скважины). Внешне это обнаруживается появлением излива жидкости из труб после отворота «свечи». Это малоприятное явление имеет мало общего с переливом жидкости из труб в процессе спуска очередной «свечи», что иногда наблюдается и что будет детально исследовано во III части данной книги. Здесь же речь идет только о том, как внутренние силы сопротивления, характеризуемые величиной θ, допускают состояние статического равновесия при h>0 в сообщающихся сосудах, какими являются трубное и заколонное пространства в скважине.

На рис. 2.4 показано количественно, на конкретном примере, как влияют на h диаметр скважины и статическое напряжение сдвига. Видно, что их влияние весьма существенно.

Дата добавления: 2018-06-27 ; просмотров: 474 ; Мы поможем в написании вашей работы!

Источник