Что называют относительной скоростью

Относительная скорость

Относительная скорость – скорость объекта В относительно А. Отображается как vAB, где А – скорость в покое В.

Галилей наблюдал концепцию сложного движения при помощи мухи и лодки. Он заметил: на борту лодки можно измерить скорость полета мухи (u). Затем можно вернуться на землю и вычислить скорость лодки (v). Но является ли скорость u фактической? Нет, потому что вы вычисляли скорость относительно лодки. Чтобы получить скорость относительно берега (s), можно использовать векторную сумму: s = u + v.

Примеры относительной скорости

Давайте рассмотрим примеры относительной скорости. Вообразите, что сидите в пассажирском поезде, отправляющимся в восточном направлении. Если посмотреть в окно и увидеть, что человек идет в ту же сторону, то покажется, что он перемещается намного медленнее. А теперь покинем поезд и посмотрим на мужчину снаружи. Сейчас кажется, что он идет вдвое быстрее, чем раньше.

Переместимся в лодку. На берегу человек шагает от одного бревна к другому. Скорость относительно берега будет обычной и ничем не выделяться. Но теперь вы оказались на берегу, а человек идет между двумя точками, но по движущейся лодке. Кажется, что его скорость намного быстрее.

Как так? Относительная скорость связана с системой координат. В случае с поездом, она двигалась в ту же сторону, что и человек, поэтому вызывала эффект замедления. Однако в неподвижной точке фиксируется реальный показатель. То же самое повторяется и с примером в лодке.

Источник

Относительная скорость.

Относительная скорость – это физическая величина, равная векторной разности скоростей, заданных относительно неподвижной системы отсчета.

При изучении механического движения в первую очередь подчеркивается его относительность. При изучении различных свойств движения тела предполагается, что рассматривается абсолютное движение (т. е. движение, отнесенное к неподвижным осям). Во многих случаях возникает необходимость определить относительное движение, отнесенное к системе отсчета, движущейся по отношению к неподвижным осям.

Относительное движение точки по отношению к подвижной системе отсчета может рассматриваться как абсолютное движение, и обладает всеми свойствами абсолютного движения.

Движение можно рассматривать в разных системах отсчета. Выбор системы отчета диктуется удобством: ее нужно выбрать так, чтобы изучаемое движение и его закономерности выглядели по возможности проще. Для перехода от одной системы отсчета к другой необходимо знать, какие характеристики движения изменяются и каким образом, а какие остаются неизменными.

Исходя из опытов можно утверждать, что при рассмотрении движений, происходящих со скоростями, малыми по сравнению со скоростью света, время неизменно во всех системах отсчета, что означает, что при измерении в любой системе отсчета промежуток времени между двумя событиями одинаков.

Что же касается пространственных характеристик, то положение тела изменяется при переходе к другой системе отсчета, однако при этом не меняется пространственное расположение этих двух событий.

Теперь рассмотрим изменение скорости движения тел при переходе от одной системы отсчета к другой, которая движется относительно первой.

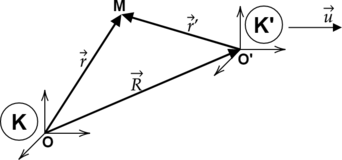
Рассмотрим пример переправы на пароме, движущемся поступательно относительно берегов (относительно земли). Вектор перемещения пассажира относительно берегов обозначим через Δr, а относительно парома – через Δr´. Перемещение парома относительно земли за то же время Δt обозначим через ΔR. В этом случае

Разделим равенство почленно на промежуток времени Δt, в течение которого произошли эти перемещения. Перейдя к пределу Δt >0, получим аналогичное соотношение для скоростей:

Из формулы (2) следует, что относительная скорость двух тел одинакова во всех системах отсчета. При переходе к новой системе отсчета к скорости каждого тела прибавляется один и тот же вектор V скорости системы отсчета. Поэтому разность векторов скоростей тел υ – υ´ не изменяется. Относительная скорость тел абсолютна.

Источник

Сложное движение точки. Теорема Кориолиса

Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где – кориолисово ускорение.

Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.

Сложное (составное) движение точки

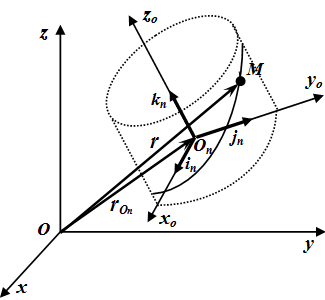
Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.

Такое движение точки называется сложным или составным.

Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.

Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).

Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.

Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела.

Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.

Относительная скорость и ускорение

Относительная скорость точки при сложном движении – это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.

Относительное ускорение точки при сложном движении – это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.

Переносная скорость и ускорение

Переносная скорость точки при сложном движении – это скорость точки, жестко связанной с телом, вызванная движением тела.

Переносное ускорение точки при сложном движении – это ускорение точки, жестко связанной с телом, вызванное движением тела.

Подставляем в (4):

.
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.

Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
,
где – угловое ускорение тела.

Абсолютная скорость и ускорение

Абсолютная скорость точки при сложном движении – это скорость точки в неподвижной системе координат.

Абсолютное ускорение точки при сложном движении – это ускорение точки в неподвижной системе координат.

Теорема о сложении скоростей

При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.

Доказательство

Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1) ;
(7)
.

Теорема Кориолиса о сложении ускорений

При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где
– кориолисово ускорение.

Доказательство

В последнем члене применим (6) и (2).

.
Тогда
.

Источник

СОДЕРЖАНИЕ

Классическая механика

В одном измерении (нерелятивистском)

В двух измерениях (нерелятивистских)

На рисунке показаны два объекта A и B, движущиеся с постоянной скоростью. Уравнения движения:

После замены и имеем: v → А | C знак равно v → А <\ displaystyle <\ vec > _ = <\ vec > _ > v → B | C знак равно v → B <\ displaystyle <\ vec > _ = <\ vec > _ >

Преобразование Галилея (нерелятивистское)

Чтобы построить теорию относительного движения, совместимую со специальной теорией относительности, мы должны принять другое соглашение. Продолжая работать в (нерелятивистском) ньютоновском пределе, мы начнем с преобразования Галилея в одном измерении:

где последняя форма имеет желаемую (легко усваиваемую) симметрию.

Специальная теория относительности

Это своеобразное отсутствие симметрии связано с прецессией Томаса и тем фактом, что два последовательных преобразования Лоренца вращают систему координат. Это вращение не влияет на величину вектора, и, следовательно, относительная скорость симметрична.

‖ v → B | А ‖ знак равно ‖ v → А | B ‖ знак равно v B | А знак равно v А | B <\ displaystyle \ | <\ vec > _ <\ mathrm > \ | = \ | <\ vec > _ <\ mathrm > \ | = v _ <\ mathrm > = v _ <\ mathrm >>

Параллельные скорости

В случае, когда два объекта движутся в параллельных направлениях, релятивистская формула для относительной скорости аналогична по форме формуле для сложения релятивистских скоростей.

Относительная скорость определяется по формуле:

Перпендикулярные скорости

В случае, когда два объекта движутся в перпендикулярных направлениях, релятивистская относительная скорость определяется формулой: v → B | А <\ displaystyle <\ vec > _ <\ mathrm >>

Относительная скорость определяется формулой

Общий случай

Общая формула для относительной скорости объекта или наблюдателя B в системе покоя другого объекта или наблюдателя A дается формулой: v → B | А <\ displaystyle <\ vec > _ <\ mathrm >>

Относительная скорость определяется формулой

Источник

Относительное движение

Скорость. Сложение скоростей.

Скорость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчета.

Единицы измерения: \(\displaystyle [\text<м>/\text<с>]\) (метр в секунду).

Правило (закон) сложения скоростей

Скорость точки относительно неподвижной системы отсчета равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы.

Рассмотрим вывод закона сложения скоростей.

Предположим теперь, что муха поползла по вагону. Тогда появляются ещё две скорости, которые нужно рассмотреть. Скорость мухи относительно вагона (то есть в движущейся системе \(\displaystyle K’\) ) обозначается \(\displaystyle \vec\) и называется относительной скоростью.

Скорость мухи относительно земли (то есть в неподвижной системе \(\displaystyle K\) ) обозначается \(\displaystyle \vec\) и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.

На вышеприведенном рисунке муха обозначена точкой M. Далее,

\(\displaystyle \vec\) — радиус-вектор точки M в неподвижной системе \(\displaystyle K\) ;

\(\displaystyle \vec\) — радиус-вектор точки M в движущейся системе \(\displaystyle K’\) ;

Источник